О.В. ХМЕЛЕВОЙ.
Донецкий национальный технический
университет
Исследование эффективности неклассических методов
спектрального оценивания применительно к задаче анализа коротких реализаций
узкополосного сигнала в гауссовом шуме.
При построении систем вокодерной
связи, анализе речи, решении задач диагностики средств телекоммуникаций
возникает необходимость в спектральном оценивании коротких реализаций
узкополосных процессов в гауссовом шуме. [1,2]. Малая длина отрезка реализации
процесса, где могут быть соблюдены условия стационарности в широком смысле, не
позволяют добиться требуемого разрешения по частоте при необходимом соотношении
сигнал/шум. Во многих случаях решения проблемы можно достичь
используя неклассические методы оценивания спектральной плотности мощности
(СПМ) исследуемого сигнала.
Известные
неклассические методы спектрального оценивания [2] позволяют решить
рассматриваемую задачу, однако требуют индивидуального подхода в выборе методов
и порядка модели. Если порядок модели выбран слишком малым, пики в оценочных
спектрах оказываются сглаженными, что снижает точность определения частоты,
если же слишком большим – то разрешающая способность СПМ возрастает, но в
спектре появляются ложные компоненты, которых нет в реальном сигнале
Данное исследование направлено на обосновании выбора метода
спектрального оценивания и определении оптимального порядка модели
применительно к задаче выявления диагностических параметров из рассматриваемого
узкополосного сигнала
Исследования выполнялись в два этапа. Первый этап
посвящен исследованию общих свойств методов для предварительного выбора метода
применительно к конкретной инженерной задаче. Эта часть экспериментов включает
исследование спектральных оценок бигармонического сигнала в гауссовом шуме.
В процессе исследования производились оценки СПМ
реализации бигармонического сигнала при использовании различных методов
спектрального оценивания различных порядков моделей. Как показатели качества
для оценки СПМ использовались соотношение сигнал-шум после обработки,
погрешность оценивания частоты и уровня гармонических компонент сигнала,
наличия паразитных компонент в оцененном спектре, устойчивость оценки. Были
рассмотрены следующие неклассические методы спектрального оценивания: метод
Берга, ковариационный метод, модифицированный ковариационный метод, метод
максимальной энтропии, метод оценивания частоты, основанный на анализе
собственных значений (Multiple Signal
Classification MUSIC). Набор методов определен в
соответствии с рекомендациями [2] и опыта их применения в технических задачах
[3].
Для сопоставления полученных оценок с результатами,
полученными с помощью классических методов, использовался также периодограмный метод [2] реализованный на основании
быстрого преобразования Фурье.
На рассмотренном этапе исследования в качестве
тестового использовался сигнал вида:
![]() ,
,
заданный m отсчетами. Количество
отсчетов выбиралось m=32, 64, 128. Уровень спектральной плотности мощности Гауссового белого шума выбирался из условия обеспечения
соотношения сигнал/шум 10дБ. В результате обработки тестовых
последовательностей установлены их следующие свойства методов:
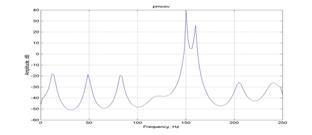
При малой длине реализации m=32 (см. рис 1,2), низком
соотношении сигнал/шум, и порядке модели 10-16 наиболее эффективен метод Берга
и модифицированный ковариационный метод. Метод Берга, однако, уступает
последнему в точности оценки частоты гармонических компонент
однако менее склонен к генерации паразитных компонент и имеет лучшее разрешение
по частоте при малом соотношении сигнал/шум. Остальные рассмотренные методы
оценивания СПМ удовлетворительного результата не показали.
При увеличении длины реализации до m=64 и том-же порядке модели,
эффективность ковариационного и модифицированного ковариационного методов
повышается даже при условии меньшего соотношения сигнал/ шум, приближаясь к
методу Берга, однако они дают большую точность по частоте. Но, наилучший
результат показывает метод MUSIC. Важно, что данный метод показывает хороший
результат при более низком порядке модели. Классические же методы в данном
случае показывают результат соизмеримый с неклассическими методами.
При увеличении количества отсчетов до 128, самые
лучшие результаты в данном эксперименте показывает классический метод БПФ и
метод MUSIC при порядке модели равной 6-7.
Результат первого этапа исследований указывает на
явное преимущество метода Берга и метода MUSIC применительно к сигналам данного
процесса, что и определило выбор для следующего этапа исследований. Второй этап
исследований ориентирован на оценку эффективности выбранных методов при анализе
спектров реальных сигналов. В качестве такого был рассмотрен фрагмент
реализации информативного сигнала диагностической системы. Реализация
воспроизводит первичный сигнал, осуществляющий амплитудно–частотную
модуляцию собственных шумов диагностирующей системы при возникновении скрытого
дефекта. Полученная информация об относительном уровне и частоте первичного
сигнала позволяет идентифицировать дефект и вынести первичный диагноз.
Результат первого этапа исследований указывает на
явное преимущество метода Берга и метода MUSIC применительно к сигналам данного
процесса, что и определило выбор для следующего этапа исследований. Второй этап
исследований ориентирован на оценку эффективности выбранных методов при анализе
спектров реальных сигналов. В качестве такого были рассмотрены фрагменты
реализации информативного сигнала диагностируемой системы. Реализация
воспроизводит первичный сигнал, осуществляющий амплитудно – частотную
модуляцию собственных шумов диагностирующей системы при возникновении скрытого
дефекта. Полученная информация об относительном уровне и частоте первичного
сигнала позволяет идентифицировать дефект и вынести первичный диагноз.
|
|
б |
Рис 1 Оценки СПМ а) по методу Берга. б)
модифицированный ковариационный метод
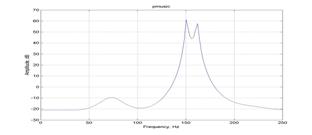
На рис 3 представлены СПМ полученные методом БПФ и
методом MUSIC (6 порядок).
|
а |
б |
Рис 2 . а) Оценка СПМ с
помощью метода БПФ; б) Оценка СПМ с помощью MUSIC.
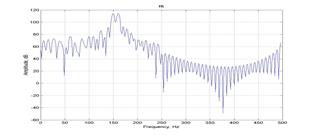
Исходная последовательность фрагмента реализации
составляет 838 отсчетов при частоте дискретизации 44 кГц. Информативная частота
в спектре первичного сигнала составляет 108 Гц Попытка обнаружить компоненту с
этой частотой в исходной реализации методом периодограммы Уэлча (см. рис 3 б),
не дает веских оснований для положительного решения. Прореживания по частоте с
целью увеличить разрешение не приводит к желаемым результатам. Использование
метода Берга к прореженной реализации так же не позволяет выявить гармоническую
компоненту на информативной частоте. Метод MUSIC обеспечивает надежное
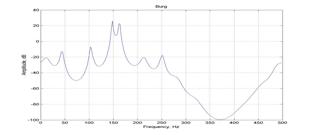
обнаружения не только информативной компоненты (108 Гц), но и более
высокочастотных составляющих, явно прослеживаемых в исходной реализации(см рис.3 а).
|
а |
б |
Рис 3 а) Исследуемый фрагмент исходной реализации; б)
Оценка СПМ по методу периодограммы Уэлча;
Выводы:
1.
При длине тестовой реализации до 32 точек наиболее целесообразно использовать
метод Берга, при большей же длине - наилучшие результаты дает метод MUSIC.
2. Все
нестандартные методы не дают объективных результатов об абсолютном уровне
гармонических компонент.
3. Метод
классификации множественных сигналов MUSIC при длине реализации всего в два
периода информативной гармонической компоненты, в числе отсчетов не более 40 и
в присутствии шумов, соизмеримых по мощности с информативными составляющими
позволяет надежно оценивать частоты и относительные уровни последних.
Список литературы
1.
Колинько Т.А. Измерения в цифровых системах связи.
Практическое руководство. – К.:ВЕК+, НТИ 2002. – 320с.
2.
Марпл – мл. С.Л. Цифровой спектральный
анализ и его приложения М.:Мир, 1990. – 584 с.
3.
Хайкин С, Карри Б.У., Кеслер
С.Б. Спектральный анализ радиолокационных мешающих отражений методом
максимальной энтропии. – ТИИЭР, №9, 1982, с51 – 62.
 а
а