В настоящее время методы цифровой обработки сигналов получили широкое распространение в телевидении, радиотехнике, системах связи, управления и контроля. Одной из самых распространённых операций при такой обработке является цифровая фильтрация сигналов.
Медианная фильтрация была предложена Тьюки в качестве инструмента сглаживания временных рядов, встречающихся в экономических исследованиях [1], а в дальнейшем она стала широко применяться при обработке изображений, речевых сигналов и т. п. Медианная фильтрация осуществляется посредством движения некоторой апертуры вдоль последовательности дискретных отсчётов и замены значения в центре апертуры медианой исходных отсчётов внутри апертуры.
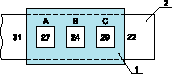
Рис. 1
Cущность медианной фильтрации с трехотсчётным окном иллюстрируется на рис. 1, где “1” — непрозрачная пластина с тремя отверстиями А, В и С; 2 — лента с наносимыми на ней отсчётами и располагаемыми с шагом, равным расстоянию между отверстиями. Лента протягивается дискретно на один шаг за один такт. В отверстиях одновременно наблюдаются три отсчёта, из которых выбирается средний. Не среднее арифметическое значение, не отсчёт в среднем отверстии, а среднее значение из трёх упорядоченно расположенных отсчётов. Так, упорядочив отсчёты, показанные на рис. 1, мы имеем значения 24, 27, 29, то есть средним является отсчёт 27 в отверстии А.
В общем случае медианой последовательности y1, y2, ... , ym (m — нечётное) является средний по значению член ряда, получаемый после упорядочения последовательности по возрастанию. Для чётного m медиана определяется как среднее арифметическое двух средних членов. В литературе можно найти и другие определения, но они мало отличаются друг от друга, а в подавляющем большинстве случаев принимают m нечётным [2].
Хотя структура одномерного цифрового медианного фильтра с трехотсчётным окном известна [3], здесь она рассматривается как пример инженерного проектирования цифрового устройства с простым и легко понятным алгоритмом работы, выполненного с применением комбинационных узлов, описанных в предыдущих статьях учебного цикла [4-7].
В цифровой системе функции отверстий А, В и С (рис. 1) выполняют три регистра А, В и С (рис. 2). Регистр А является регистром данных какого-либо устройства, работающего в условиях сильных промышленных помех, например, преобразователя температуры в цифру. Все эти регистры имеют единую систему синхронизации, обеспечивающую запись данных в регистр А, загрузку содержимого регистра А в регистр В и содержимого регистра В в регистр С. Перед началом процедуры фильтрации все регистры обнуляются. Началом процедуры является момент появления первого отсчёта в регистре А. Так, например, если входная последовательность имеет вид 22, 29, 24, 27, 31, 40, 28, 32, 29,... (22 — первый отсчёт), то в первом такте будем иметь следующие значения отсчётов: А = 22, В = 0, С = 0, откуда следует, что средний отсчёт равен 0. Во втором такте будем иметь А = 29, В = 22, С = 0, откуда следует, что средний отсчёт равен 22 и т. д. Итак, выходная последовательность будет иметь вид: 0, 22, 24, 27, 27, 31, 31, 32, 29,... .

Рис. 2
Очевидно, что медианный фильтр с трехотсчётным окном осуществляет задержку выходной последовательности на один такт по отношению к входной.
Кроме указанных регистров аппаратная реализация такого фильтра должна включать в себя n-разрядный мультиплексор MS 4->1, в котором будут использоваться только три информационных входа (n — число двоичных разрядов цифрового отсчёта), и три цифровых компаратора, обеспечивающих сравнение каждого отсчёта с каждым, что можно рассматривать как замену процедуры упорядочения. Это позволяет снизить аппаратные затраты и время вычисления медианы. Напомним, что упорядочение требует выполнения операций сравнения и перестановки отсчётов.
Отметим прежде всего, что нет необходимости учитывать отношения равенства отсчётов, так как при равенстве двух или трёх отсчётов любой из них может рассматриваться как средний. Выберем соотношения A > B, A > C, B > C, обозначив соответствующие сигналы с выходов трёх цифровых компараторов переменными x2, x1 и x0. Примем, что если указанные соотношения выполняются, то соответствующие выходные сигналы компараторов принимают значение “1”, если не выполняются, то — “0”. Итак, задача проектирования нашего фильтра сводится к выявлению структуры комбинационной схемы (КС), реализующей адресные переменные а1 и а0 мультиплексора MS 4->1, обеспечивающего автоматическую передачу среднего отсчёта из трёх, поступивших на его информационные входы.
Оформим таблицу, в которой представлены: № набора — десятичный эквивалент двоичного набора трёх переменных x2, x1 и x0; комментарий — это условная гистограмма из трёх отсчётов А, В и С, качественно соответствующая ситуации, отражённой одним из восьми наборов переменных x2, x1 и x0; в столбце “средний отсчёт” указывается средний отсчёт, выявленный из соответствующей гистограммы. Так, в первой строке имеем набор x2x1x0 = 000, из которого следует, что A < B, A < C, B < C. Эта ситуация качественно показана в столбце “комментарий”, из которого следует, что в данном случае средним является отсчёт В. Так как на рис. 2 отсчёт В поступает на вход D1 MS 4->1, то в этой строке указываем значения а1 = 0, а0 = 1 (первый вариант кодирования адресных переменных в таблице). При наборе x2x1x0 = 001 имеем ситуацию A < B, A < C, B > C, которая отражена соответствую-щей гистограммой, а из послед-ней следует, что средним отсчётом в данном случае является отсчёт С. Соответственно устанавливаем а1 = 1, а0 = 0.
Таблица
№ наб. х2
А>Вх1
А>Сх0
В>ССредний отсчет 1 вариант 2 вариант а1 а0 а1 а0 0 0 0 0 В 0 1 0 0 1 0 0 1 С 1 0 1 0 2 0 1 0 - х х х х 3 0 1 1 А 0 0 0 1 4 1 0 0 А 0 0 0 1 5 1 0 1 - х х х х 6 1 1 0 С 1 0 1 0 7 1 1 1 В 0 1 0 0 Набор x2x1x0 = 010 никогда не будет появляться на выходах цифровых компараторов, так как он соответствует невозможной ситуации A < B, A > C, B < C, поэтому в соответствующей строке таблицы адресные переменные а1 и а0 обозначены крестиком как безразличные значения. Аналогично заполняются все строки таблицы. Рассматривая а1 и а0 как функции алгебры логики от переменных x2, x1 и x0 и используя для их минимизации карты Карно (рис. 3) [8], получаем
а1 = x1 Е x0 (1)
а0 = x2 Е x0 или x2 Е x0. (2)Попытаемся устранить инвертор, необходимый для реализации x2 или x0 в формуле (2). Для этого перекодируем адресные переменные а1 и а0, приняв, что отсчёт А подаётся на вход D1, а В — на вход D0 MS 4®1 (второй вариант в таблице). На рис. 4 приведены карты Карно для второго варианта кодирования адресных переменных а1 и а0, из которых следует:
а1 = x1 Е x0 (3)
а0 = x2 Е x1.
(4)
Рис. 3
Рис. 4
Очевидно, что второй вариант кодирования предпочтительнее. Итак, комбинационная схема (КС), структуру которой мы определили, представляет из себя два элемента “сумма по mod2”.
Убедимся в справедливости отмеченного выше замечания о том, что нет необходимости учитывать соотношения равенства. Рассмотрим следующие ситуации:
- А = В, A > C, в этом случае x2x1x0 = 011, средний отсчёт А;
- А = В, A < C, в этом случае x2x1x0 = 000, средний отсчёт В;
- А = С, A > В, в этом случае x2x1x0 = 100, средний отсчёт А;
- А = С, A < B, в этом случае x2x1x0 = 001, средний отсчёт C;
- B = C, A > B, в этом случае x2x1x0 = 110, средний отсчёт C;
- B = C, A < B, в этом случае x2x1x0 = 000, средний отсчёт B;
- А = В = C, в этом случае x2x1x0 = 000, средний отсчёт В.
Если на выходах цифровых компараторов используются соотношения “больше или равно”, то будем иметь:
- А = В, A > C, в этом случае x2x1x0 = 111, средний отсчёт В;
- А = В, A < C, в этом случае x2x1x0 = 100, средний отсчёт А;
- А = С, A > В, в этом случае x2x1x0 = 110, средний отсчёт С;
- А = С, A < B, в этом случае x2x1x0 = 011, средний отсчёт А;
- B = C, A > B, в этом случае x2x1x0 = 111, средний отсчёт В;
- B = C, A < B, в этом случае x2x1x0 = 001, средний отсчёт С;
- А = В = C, в этом случае x2x1x0 = 111, средний отсчёт В.
Достоинства и недостатки медианных фильтров
Достоинства
- простота пструктуры, позволяющая легко реализовать фильтр как аппаратными, так и программными средствами;
- медианный фильтр не влияет на ступенчатые и пилообразные функции;
- этот фильтр хорошо подавляет одиночные импульсные помехи (случайные шумовые выбросы отсчетов и промахи);
- концепцию медианного фильтра легко обобщить на два измерения, применяя двухмерное окно желаемой формы (прямоугольное, крестообразное, кольцевое, круговое).
Недостатки
- медианная фильтрация - метод нелинейной обработки сигналов, так как медиана суммы двух произвольных последовательностей не равна сумме их медиан. Это усложняет математический анализ их характеристик. Нельзя разграничить влияние этих фильтров на сигнал и шум, что для линейных фильтров делается очень просто;
- фильтр вызывает уплощение вершин треульной функции;
- подавление гауссовского шума менее эффективно, чем у линейных фильтров;
- двумерная обработка приводит к более существенному ослаблению сигнала
Проведённый анализ подтверждает то, что при проектировании структуры комбинационной схемы КС можно использовать на выходах цифровых компараторов любые комбинации соотношений “больше”, “больше или равно”, “меньше”, “меньше или равно”. Из всего вышеописанного и с учетом указанных недостатков можно сделать вывод о не целесообразности использования данного метода фильтрации к образцам снимков клеток нетрофилов рассматриваемых в магистерской работе.
Литература
- Tukey J.W. Exploratory Data Analisis (Addison - Wesley, Reading, Mass., 1971).
- Быстрые алгоритмы в цифровой обработке изображений / Т.С. Хуанг, Дж.-О. Эклунд, Г.Дж. Нуссбаумер и др.; Под ред. Т.С. Хуанга: Пер. с англ. — М.: Радио и связь. — 1984. —224 с.
- Устройство для выделения медианы трех чисел. А. С. №1575168.
- Воробьев Н.В. Мультиплексоры // Chip News. — 1998. — № 11-12. — С. 38–41.
- Воробьев Н.В. Мультиплексор как многофункциональный узел // Chip News. — 1999. — № 2. — С. 36–41.
- Воробьев Н.В. Цифровые компараторы // Chip News. — 1999. — № 5. — С. 8–14.
- Воробьев Н.В. Цифровые компараторы (продолжение) // Chip News. — 1999. — № 7. — С. 35–38.
- Воробьев Н.В. Минимизация функций алгебры логики // Chip News. — 1997. — № 9-10. — С. 54–60.
- Прэтт У. Цифровая обработка изображений: Пер. с англ. — М.: Мир. — 1982. — Кн. 2. — 480 с. (Кн. 1. — 312 с.).