Рис. 5.
3.1. Общие соображения и определения.
Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации
| f(x) ® min, | (1) |
где f: Rm ® R,
укладываются в следующую грубую схему. Начиная с некоторого
| f(xn+1) < f(xn) | (2) |
при всех n О N. Такие последовательности иногда называют релаксационными, а методы построения релаксационных последовательностей — итерационными методами или методами спуска. Последовательность, удовлетворяющую (2), строят в надежде, что уменьшая на каждом шаге (переходе от xn к xn+1) значение функции, мы приближаемся к минимуму (по крайней мере, локальному).
Мы будем говорить, что метод, начиная с данного x0 О Rm,
а) условно сходится, если последовательность {xn} релаксационна и
| f ў(xn) ® Q при n ® Ґ; |
б) сходится, если
| xn ® x* = argmin f(x) при n ® Ґ; |
в) линейно сходится (или сходится со
скоростью геометрической прогрессии, или имеет первый порядок
сходимости), если при некоторых
| ||xn - x*|| Ј Cqn; | (3) |
г) сверхлинейно сходится, если для любого
д) квадратично сходится (или имеет второй
порядок сходимости), если при некоторых
| ||xn - x*|| Ј Cq2n. |
Если эти свойства выполняются только для x0 достаточно близких к x*, то как всегда добавляется эпитет "локально".
З а д а ч а 3.1*. Пусть при некотором q О [0, 1)
| ||xn+1 - x*|| Ј q||xn - x*||, n О N. |
Докажите, что метод линейно сходится.
З а д а ч а 3.2*. Пусть при некотором C1 > 0
| ||xn+1 - x*|| Ј C1||xn -x*||2, n О N |
и ||x0 - x*|| достаточно мала. Докажите, что метод квадратично сходится.
Будем говорить, что на данной последовательности метод сходится с порядком p (или имеет p-ый порядок сходимости), если при некотором C
| ||xn+1 - x*|| Ј C||xn - x*||p. |
3.2. Эвристические соображения, приводящие к градиентным методам.
Выше уже отмечалось, что если x не является точкой локального минимума функции f, то двигаясь из x в направлении, противоположном градиенту (еще говорят, в направлении антиградиента), мы можем локально уменьшить значение функции. Этот факт позволяет надеяться, что последовательность {xn}, рекуррентно определяемая формулой
| xn+1 = xn - af ў(xn), | (4) |
где a - некоторое положительное число, будет релаксационной.
К этой же формуле приводит и следующее рассуждение. Пусть у нас есть
некоторое приближение xn. Заменим в шаре
| f(x) » j(x) |
(функция j аппроксимирует f в окрестности
точки xn с точностью o(x
- xn)). Разумеется,
(линейная) безусловная задача
|
З а д а ч а 3.3. Покажите, что argminx
О B(xn, e)f(x) задается формулой (4)
с |
3.3. Градиентный метод с постоянным шагом.
В общем случае число a в формуле (4) может
на каждом шаге (
| xn+1 = xn - anf ў(xn). | (5) |
Именно методы, задаваемые формулой (5),
называются градентными. Если
Поясним геометрическую суть градиентного метода. Для этого мы выберем способ
изображения функции с помощью линий уровня. Линией уровня
функции f (изолинией) называется любое множество вида

З а д а ч а 3.4. Докажите, что касательная к линии
уровня функции
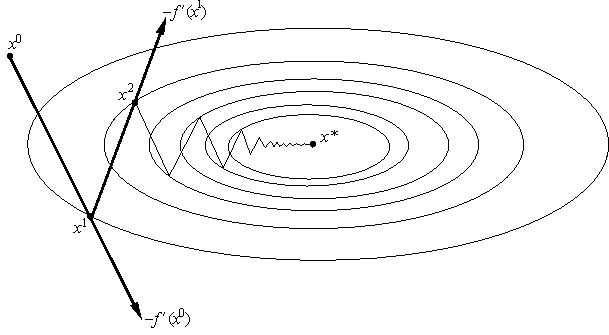
Геометрическая интерпретация градиентного метода с постоянным шагом изображена на рис. 6. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в a раз".
3.4. Один пример исследования сходимости.
Изучим сходимость градиентного метода с постоянным шагом на примере функции
| f(x) = |x|p, |
где p > 1 (случай p Ј 1 мы не
рассматриваем, поскольку тогда функция f не будет гладкой, а мы такой
случай не исследуем). Очевидно, задача (1) с
такой функцией f имеет единственное решение
| xn+1 = xn - ap|xn|p-1sign xn. | (6) |
Пределом этой последовательности может быть только 0. Действительно, если
| x** = x** - ap|x**|p-1sign x**, |
откуда x** = 0. Очевидно также, что если
Покажем, что если p < 2, то при любом шаге
| |xn+1| > |xn|. | (7) |
Поэтому, если xn не обращается в нуль, то она не может сходиться к нулю и, следовательно, не может сходиться вообще.
З а д а ч а 3.5. Докажите.
Таким образом, осталось доказать (7). В силу (6)
| |xn+1| = |xn - ap|xn|p-1 ·sign xn| = |xn|·| 1 -ap|xn|p-2·sign xn|. |
Остается заметить, что если
З а д а ч а 3.6. Покажите, что число начальных точек x0, для которых xn обращается в нуль при некотором n (и следовательно, при всех бóльших), не более чем счетно.
Если p = 2,
| |xn+1| = |xn|·|1 - 2a|. |
Поэтому, если
| |xn+1| = |1 - 2a|n+1·|x0| ® 0 при n ® Ґ. |
Если же a і 1, то
| |xn+1| і |xn|, |
и последовательность {xn}, начинающаяся из ненулевой начальной точки, расходится.
З а д а ч а 3.7. Докажите, что если p > 2,
то градиентный метод (6)
сходится при
Таким образом, есть функции, для которых градиентный метод не сходится даже при сколь угодно малом шаге a и есть функции, для которых он сходится только при достаточно малых шагах. В следующих пунктах мы приведем ряд теорем о сходимости градиентного метода.
3.5. Теорема об условной сходимости градиентного метода с постоянным шагом.
Пусть в задаче (1) функция f ограничена снизу, непрерывно дифференцируема и, более того, f ў удовлетворяет условию Липшица:
| ||f ў(x) - f ў(y)|| Ј L ||x - y|| при всех x, y О Rm. |
Тогда при a О (0, 2/L) градиентный метод с постоянным шагом условно сходится.
Д о к а з а т е л ь с т в о. Положим
| jў(t) = (f ў(xn + tzn), zn) |
и поэтому по формуле
| f(xn+1) - f(xn) = f(xn + zn) - f(xn) = j(1) - j(0) = |
|
|
Добавив и отняв |
|
|
Учитывая условие Липшица для f ў, эту цепочку можно продолжить:
|
(8) |
Поскольку 1 - La/2 > 0,
последовательность {f(xn)} не возрастает и,
следовательно, релаксационность
|
Подчеркнем, что теорема
3.5 не гарантирует сходимости
метода, но лишь его условную
сходимость, причем, локальную.
Например, для функции
З а д а ч а 3.8. Докажите.
Поскольку в теореме
3.5 градиент непрерывен, любая предельная точка последовательности
{xn} является стационарной.
Однако эта точка вовсе не обязана быть точкой минимума, даже локального.
Например, рассмотрим для функции
Заметим также, что описанный метод не различает точек локального
и глобального
минимумов. Поэтому для того, чтобы сделать заключение о сходимости
xn к точке
3.7. Теорема о линейной сходимости градиентного метода с постоянным шагом.
Пусть выполнены условия теоремы
3.5 и, кроме того, f дважды непрерывно дифференцируема и сильно
выпукла с константой l. Тогда при
| ||xn - x*|| Ј qn||x0 - x*||. |
Д о к а з а т е л ь с т в о. Решение
|
или, для x = x* и y = xn,
учитывая, что
|
(9) |
(здесь мы, как и выше, воспользовались задачей
2.3). Далее, в силу утверждения (2.5) из
п. 2.3
| l||h||2 Ј (f ўў[x* + s(xn -x*)]h, h) Ј L ||h||2, |
выполнено неравенство
|
(10) |
Интеграл, стоящий в этом неравенстве, определяет линейный (симметричный
в силу симметричности f) оператор на Rm,
обозначим его Ln. Неравенство (10)
означает, что
| xn+1 = xn - aLn(xn - x*). |
Но тогда
| ||xn+1 -
xn|| = ||xn - x* -aLn(xn - x*)|| = = ||(I - aLn)(xn - x*)|| Ј ||I - aLn |
Спектр
| 1 - al і si і 1 - aL, |
и следовательно (см. неравенство (2.4))
| ||I - aLn|| Ј max{|1 -al|, |1 - aL |} = q. |
Таким образом,
| ||xn+1 - xn|| Ј q||xn - x*||. |
Из этого неравенства и задачи 3.1 вытекает утверждение теоремы.
3.8. Об оптимальном выборе шага.
Константа q, фигурирующая в теореме 3.7 и характеризующая скорость сходимости метода, зависит от шага a. Нетрудно видеть, что величина
| q = q(a) = max{|1 - al|, |1 - aL |} |
минимальна, если шаг a выбирается из условия
|
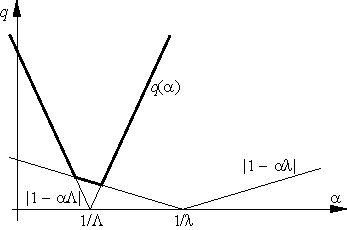
Напомним (см. п. 2.3),
что в качестве l и L могут
выступать равномерные по x оценки сверху и снизу собственных значений
оператора
| f(x1, x2) = lx21+ L x22с l << L. |

Поведение итераций градиентного метода для этой функции изображено на
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Мы опишем сейчас два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.
3.9. Градиентный метод с дроблением шага.
В этом варианте градиентного метода величина шага an на каждой итерации выбирается из условия выполнения неравенства
| f(xn+1) = f(xn - anf ў(xn)) Ј f(xn) - ean||f ў(xn)||2, | (11) |
где
З а д а ч а 3.9. Докажите (воспользуйтесь неравенством (8)).
З а д а ч а 3.10. Сходится ли градиентный метод с
дроблением шага для функции
Можно показать, что в условиях теоремы 3.7 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора a на каждом шаге, заменяя ее на проблему выбора параметров e, d и a0, к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.
3.10. Метод наискорейшего спуска.
Этот вариант градиентного метода основывается на выборе шага из следующего
соображения. Из точки xn будем двигаться в направлении
антиградиента
до тех пор пока не достигнем минимума функции f на этом направлении,
| an = argminaО[0, Ґ)f(xn - af ў(xn)). | (12) |
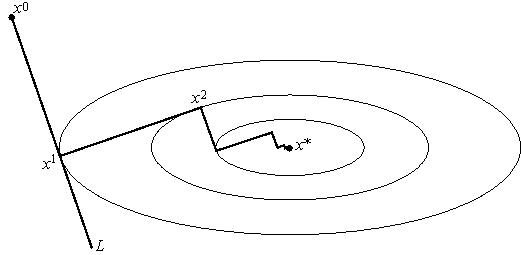
Другими словами, an выбирается так,
чтобы следующая итерация была точкой минимума функции f на луче L
(см. рис.
9). Такой вариант градиентного метода называется методом наискорейшего
спуска. Заметим, кстати, что в этом методе направления соседних шагов
ортогональны. В самом деле, поскольку функция
|
| = (f ў(xn - anf ў(xn)), -f ў(xn)) = -(f ў(xn+1), f ў(xn)). |
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации (12). Такие задачи будут обсуждаться ниже. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
З а д а ч а 3.11. Докажите, что если
|
З а д а ч а 3.12. Пусть