Навигация
ПРИМЕНЕНИЕ ЛИНЕЙНОГО ГЕНЕТИЧЕСКОГО ПРОГРАММИРОВАНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ОПЕАРТОРА КОРРЕКЦИИ ИНЕРЦИОННОСТИ ИЗМЕРИТЕЛЬНОГО КАНАЛА ТЕМПЕРАТУРЫ
Савков Д. А., Светличная В.А., к.т.н., доц. каф. АСУ
Донецкий национальный технический университет
Факультет компьютерных информационных технологий и автоматизации
Abstract
Savkov D., Svetlichnay V. Applying of linear genetic programming for definition of the operator of correction of an inertance of a counting channel of temperature. In the article the analysis of methods of correction of dynamic inaccuracy of metering devices of a hydrophysical system is given and the new method of looking up of the correcting operator is offered.
В последние годы, в связи с проведением в широких масштабах исследований Мирового океана, возникла проблема обработки массовой океанографической информации. Экспериментальное изучение океана связано с осуществлением дорогостоящих морских экспедиций, и основные затраты материальных средств в океанографии относятся к этапу исследований, состоящему в проведении наблюдений, их обработки и теоретическом анализе. Это выдвинуло перед океанографами новую задачу – задачу оптимизации наблюдений, заключающуюся в том, чтобы получить нужные представления о закономерностях процессов в океане при минимальном количестве измерений.
Основными гидрофизическими параметрами водной среды являются температура – Т, удельная электрическая проводимость УЭП –
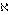 ,
давление – Р и скорость – V. Они являются первичными, так как определяются прямыми измерениями. Значительная часть характеристик определяется косвенно, путем расчетов по непосредственно измеряемым параметрам. Среди вторичных параметров наиболее важными являются концентрация солей (соленость – S) и плотность
,
давление – Р и скорость – V. Они являются первичными, так как определяются прямыми измерениями. Значительная часть характеристик определяется косвенно, путем расчетов по непосредственно измеряемым параметрам. Среди вторичных параметров наиболее важными являются концентрация солей (соленость – S) и плотность
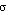 ,
водной среды.
,
водной среды.
Для измерения первичных параметров используются информационно-измерительные системы океанографических и гидроэкологических исследований (ИИС), снабженные соответствующими измерительными каналами. Канал включает первичный измерительный преобразователь (ПИП) и измерительный канал (ИК), представляющий собой преобразовательно-усилительную схему, выходной параметр которой (напряжение, ток, код и т.п.) связан с измеряемой физической величиной некоторой функцией, называемой градуировочной характеристикой. Принципы действия этих каналов базируются на различных методах измерений. Это обусловлено тем, что каждый из методов дает удовлетворительные результаты лишь в определенном диапазоне параметров исследуемых сред.
В автоматизированных зондовых информационно-измерительных системах вследствие последовательного опроса измерительных каналов условие полной синхронности измерения параметров Т,
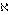 и Р на практике не выполняется. Основными доминирующими причинами погрешностей при определении вторичных параметров – солености, плотности и т.д. в режиме зондирования являются различные динамические характеристики измерительных каналов, обусловленные различной инерционностью первичных измерительных преобразователей, и последовательным способом ввода первичных параметров. Поскольку преобразователи электрической проводимости и давления существенно менее инерционны относительно термометра сопротивления, то основным источником динамической погрешности является ПИП температуры.
и Р на практике не выполняется. Основными доминирующими причинами погрешностей при определении вторичных параметров – солености, плотности и т.д. в режиме зондирования являются различные динамические характеристики измерительных каналов, обусловленные различной инерционностью первичных измерительных преобразователей, и последовательным способом ввода первичных параметров. Поскольку преобразователи электрической проводимости и давления существенно менее инерционны относительно термометра сопротивления, то основным источником динамической погрешности является ПИП температуры.
Таким образом возникла задача коррекции показаний датчиков температуры.
В настоящее время в литературе предлагается ряд методов коррекции, которые можно разделить на две группы: аппаратные и программные.
Аппаратные методы предусматривают либо использование дополнительных датчиков температуры, либо снижение скорости зондирования, что в свою очередь приводит к увеличению стоимости эксперимента.
К программным методам уменьшения погрешности канала температуры относится метод коррекции по трем точкам, описанный в /1/ и реализованный в устройстве /2/. В статье /3/ описывается метод коррекции, учитывающий переходную характеристику датчика. Эти методы не дают высокой точности, так как первый метод проводит интерполяцию по данным, которые содержат ошибку, связанную с инерционностью датчика, а второй метод не учитывает скорость зондирования.
Конечной целью большей части исследований в области физической океанографии является получение представлений об изучаемой характеристике океана
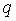 как функции четырех переменных
как функции четырех переменных
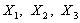 ,
,
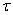 , где
, где
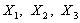 ,
- пространственные характеристики,
,
- пространственные характеристики,
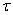 - время, а также о закономерностях взаимосвязи величины
- время, а также о закономерностях взаимосвязи величины
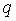 с другими гидрофизическими параметрами, которые могут быть положены в основу прогностических задач. Величина
с другими гидрофизическими параметрами, которые могут быть положены в основу прогностических задач. Величина
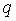 в каждой конкретной задаче по своему смыслу является результатом преобразования некоторой соответствующей исходной физической величины
в каждой конкретной задаче по своему смыслу является результатом преобразования некоторой соответствующей исходной физической величины
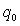

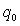 , а получаем
, а получаем

>В связи с потерей информации при измерении точное нахождение значение
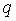 по
по
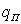 в общем случае невозможно. Поэтому в ходе обработки данных наблюдений производится лишь приближенное преобразование
в общем случае невозможно. Поэтому в ходе обработки данных наблюдений производится лишь приближенное преобразование
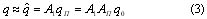
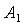 с помощью которого величину
с помощью которого величину
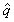 можно максимально приблизить к
можно максимально приблизить к
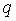 , необходимо найти вид оператора
, необходимо найти вид оператора
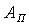 , описывающего действие прибора на исходную величину.
Под
, описывающего действие прибора на исходную величину.
Под 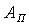 подразумевается преобразование исходной величины вплоть до ее поступления на ЭВМ для обработки, при этом оператор
подразумевается преобразование исходной величины вплоть до ее поступления на ЭВМ для обработки, при этом оператор
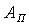 включает также действие помех в канале передачи информации и преобразование ее в аппаратуре с целью защиты от помех.
включает также действие помех в канале передачи информации и преобразование ее в аппаратуре с целью защиты от помех.
Применим данные рассуждения к проблеме коррекции показаний датчика температуры. Тогда формулы (2) и (3) примут вид
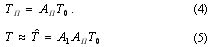
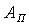 это оператор воздействия инерционности датчика температуры, переходная характеристика которого описывается дифференциальным уравнением:
это оператор воздействия инерционности датчика температуры, переходная характеристика которого описывается дифференциальным уравнением:
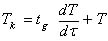
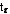 - постоянная времени переходного процесса датчика температуры. Задача заключается в том, чтобы найти, такой оператор
- постоянная времени переходного процесса датчика температуры. Задача заключается в том, чтобы найти, такой оператор
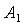 , который бы компенсировал
, который бы компенсировал
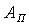 .
.
Для определения оператора
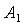 будем использовать метод линейного генетического программирования. С помощью генетического программирования производится поиск оптимальной программы, описывающей требуемую зависимость.
будем использовать метод линейного генетического программирования. С помощью генетического программирования производится поиск оптимальной программы, описывающей требуемую зависимость.
Линейное генетическое программирование ориентировано на алгоритмические языки высокого уровня, и заключается в том, что каждая особь-программа представляется последовательностью операторов различной длины. Здесь множество команд или операторов состоит из арифметических операторов, условных операторов и вызовов функций. При таком подходе каждый оператор кодируется четырехмерным вектором, компонентами которого являются тип оператора и адреса переменных. Такое представление позволяет выполнять эффективно рекомбинацию (скрещивание) программ и их интерпритацию. При этом обычно используется турнирный метод отбора родителей в промежуточную популяцию.
Рассмотрим двухточечный оператор кросенговера используемый при скрещивании программ (рис. 1). В обоих родителях выбираются сегменты программ начинающиеся со случайных позиций и имеющие случайно определенную длину. Затем производится обмен выбранными сегментами программ родителей. Если размер хотя бы одного из потомков превышает заданный порог, результаты оператора кросенговера анулируются и скрещивание выполняется с равными по размеру фрагментами.
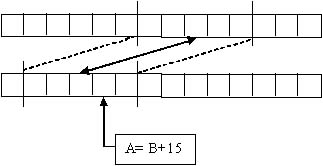
Оператор мутации случайно заменяет тип оператора, переменную или значение константы из допустимых значений.
Алгоритм работает до тех пор, пока не будет найдена зависимость (функция), которая с заданной точностью будет повторять результаты, полученные опытным путем.
В нашем случае для определения оператора
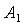 с помощью линейного генетического программирования необходимо получить такие данные, как показания стационарно установленного датчика температуры и показания датчика температуры движущегося с какой либо скоростью в тот момент, когда он будет находиться на той же глубине, что и стационарно установленный датчик. Для этого выполним следующий опыт. Располагаем, ряд стационарных датчиков на различной глубине и несколько раз опускаем датчик температуры, изменяя скорость движения датчика от опыта к опыту.
с помощью линейного генетического программирования необходимо получить такие данные, как показания стационарно установленного датчика температуры и показания датчика температуры движущегося с какой либо скоростью в тот момент, когда он будет находиться на той же глубине, что и стационарно установленный датчик. Для этого выполним следующий опыт. Располагаем, ряд стационарных датчиков на различной глубине и несколько раз опускаем датчик температуры, изменяя скорость движения датчика от опыта к опыту.
Создаем популяцию особей-программ. Предполагаем, что данные особи-программы описывают зависимость показаний инерционного движущегося и стационарно установленных датчиков с учетом скорости. Применяем оператор кросенговера и мутации для данной популяции пока не будет найдена программа, которая бы с заданной точность исправляла показаний движущегося датчика.
Данный метод показал не плохие результаты при моделировании оператора
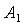 для корректировки показаний датчика температуры. Но поскольку для проверки использовались данные не учитывающие микротурбулентную структуру гидрофизических полей в дальнейшем предполагается использовать данный метод вместе с методами планирования эксперимента, который позволит минимизировать погрешность от влияния микротурбулентности.
для корректировки показаний датчика температуры. Но поскольку для проверки использовались данные не учитывающие микротурбулентную структуру гидрофизических полей в дальнейшем предполагается использовать данный метод вместе с методами планирования эксперимента, который позволит минимизировать погрешность от влияния микротурбулентности.
1. Парамонов В. М., Кушнир В. И., Забурдаев В. К. Современные методы и средства измерения гидрологических параметров океана. – Киев: Наукова думка, 1979. – 260 с.
2. А. с. 1612718 СССР, МКИ4 G01V1/38. Зондирующее устройство для измерения параметров водной среды./ А. А. Зори, А. В. Зимин, С. В. Мащенко, Е. О. Савкова (СССР). – Заявл. 03.05.89., Зарегистр. 08.08.90.
3. Зори А. А., Савкова Е. О. Методы уменьшения динамической погрешности гидрофизических информационно-измерительных систем. Сб. статей
4. Парамонов В. М., Кушнир В. И., Заикин В. М. Автоматизациягидрофизического эксперимента. – Л.: Гидрометеоиздат, 1982. – 224 с.