Как правило, моделирование случайной величины с заданным распределением осуществляется путем преобразования одного или нескольких независимых значений случайного числа, равномерно распределенного в интервале (0,1), т.е. по формуле

      Последовательность "выборочных" значений обычно получается с помощью теоретико-числовых алгоритмов, из которых наиболее часто используется так называемый метод вычетов (конгруэнтный генератор) в форме

      Здесь r, как правило, число двоичных разрядов, используемых для представления числа в компьютере, М - достаточно большое число, взаимно-простое с 2 ^r. Величину М назовем множителем генератора. Величины a_n такого типа называются псевдослучайными числами ; они проверяются статистическим тестированием, специальными аналитическими исследованиями и решением типовых задач. Для генератора длина периода последовательности {a_n} равна 2 ^r-2.

      Для коррелирования результатов рашения различных задач целесообразен следующий порядок использования псевдослучайных чисел. Последовательность u_n предварительно разбивается на подпоследовательности длины m, начинающиеся с чисел u_km, k = 0,1,2... (т.е., с начальных значений последовательностей) и каждая подпоследовательность используется для построения соответствующих "выборочных траекторий" моделируемого процесса. Значение m должно выбираться из тех соображений, что m псевдослучайных чисел практически достаточно для построения одной траектории. Ясно, что для метода вычетов начальные значения u_km указанных подпоследовательностей получаются по формуле

      Итак, для моделирования k-й траектории используется подпоследовательность метода вычетов, начинающаяся с

      Такой способ распределения случайных чисел по испытаниям назовем lf-генератором (сокращение от "little-frog"-генератор). При этом множитель М_m для вспомогательного генератора, обеспечивающего "прыжки" с шагом длины m, вычисляется на основе равенства

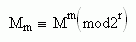
      Очевидно, что отличие обычного способа распределения случайных чисел "подряд" (т.е. в порядке обращения к генератору), lf-генератор обеспечивает малое изменение результатов моделирования при малом изменении параметров задачи. В связи с этим, lf-генератор более корректно проверяется решением типовых задач по сравнению с обычным генератором.

      Ясно, что рассмотренный модифицированный генератор позволяет также распределить псевдослучайные числа между отдельными процессорами, но при этом надо осуществлять "прыжки" значительно большей длины. Точнее говоря, для этого следует заменить величину m на u = mN, где N - количество траекторий, которые практически моделируются на одном процессоре. Получаемый таким образом "крупномасштабный" генератор будем называть bf-генератором (сокращение от big-frog-генератор)

      Рассмотрим теперь возможность комбинирования псевдослучайных последовательностей с физическими генераторами случайных чисел. Ясно, что вместо начальных чисел a_km, соответствующих отдельным траекториям, можно подставлять числа из физических генераторов. Такой комбинированный метод допускает теоретическое обоснование при

      Отметим, что распределение "физических" случайных чисел можно существенно улучшать с помощью суммирования по модулю единица (коргруэнтного суммирования), то есть используя выражение

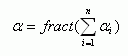
,где a_i-числа из физического генератора. Известно, что распределение величины a очень быстро сходится к равномерному распределению при .

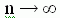      Более того, поэлементное конгруэнтное суммирование независимых последовательностей "настоящих" случайных чисел эффективно улучшает многомерную равномерность.