ПРИЛОЖЕНИЕ А

ЭЛЕМЕНТЫ СПЕКТРАЛЬНОЙ ТЕОРИИ ПОГЛОЩЕНИЯ ИК-ИЗЛУЧЕНИЯ ГАЗАМИ

     Методы качественного и количественного анализа состава веществ, основанные на способности веществ избирательно поглощать оптическое излучение, получили широкое применение при решении всевозможных аналитических задач в промышленности, научных исследованиях и при контроле за состоянием окружающей среды. Указанные методы являются разделом абсорбционной спектроскопии. Спектры поглощения характеризуют строение поглощающего вещества, тогда как решение аналитических задач требует знания не всего спектра, а лишь отдельных, наиболее характерных для определяемых компонентов среды интервалов частот.

     Энергию изолированной молекулы можно представить в виде:

(А-1)

     где учтены энергия поступательного движения, которая зависит от скорости движения и может принимать любые значения, а также энергия электронов валентного уровня, энергия колебательного и вращательного движения молекулы (все последние принимают только значения квантовых уровней).

     Рассматривая и учитывая взаимодействие различных видов движения молекул, баланс энергии принимает вид:

(А-2)

     здесь последние три члена учитавают взаимодействие различных видов движения молекулы.

     Величины электронной, колебательной и вращательной энергий молекулы имеют различный порядок. Энергия электронных переходов имеет порядок нескольких электроновольт, колебательная энергия измеряется десятыми и сотыми долями электроновольт, вращательная энергия - тысячными и десятитысячными долями электроновольт. Соответственно величине энергии электронные спектры занимают ультрафиолетовую и видимую части спектра, колебательные - ближнию инфракрасную, вращательные - далекую инфракрасную и микроволновую. Поскольку в процессе движения молекулы и ее взаимодействия с другими молекулами происходит изменение одновременно всех трех составляющих энергии одновременно, то в чистом виде колебательные спектры не проявляются. Таким образом, в зависимости от диапазона длин волн мы имеем дело либо с электронно-колебательно-вращательными, либо с колебательно-вращательными, либо с чисто вращательными спектрами. Колебательно-вращательная полоса содержит некоторое множество спектральных линий поглощения.

     Cпектр одиночной линии. Квантовая механика дает следующее выражение для контура спектральной линии:

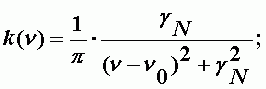(А-3)

     g_N - естественная ширина линии; определяется на уровне 0.5;

     Уширение спектральной линии за счет эффекта Доплера. Имеет место максвеллово распределение молекул по скоростям. Для контура спектральной линии получается выражение:

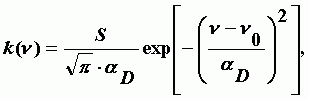(А-4)

     где S - интенсивность линии;
           a_D- доплеровская полуширина спектральной линии;

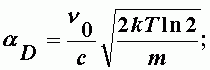(А-5)

     где Т - абсолютная температура;
           m - масса молекулы;
           с - скорость света;
           k - постоянная Больцмана.

     Для линии вращательной полосы H₂O около 200 см^-1:

      a_D = 3,5·10^-4 см^-1.

     Уширение спектральной линии за счет столкновений молекул. Этот параметр напрямую обусловлен давлением: с ростом давления растет интенсивность столкновений. Теория Лоренца дает следующее описание спектральной линии (в литературе часто называемым дисперсионным контуром):

(А-6)

     Полуширина линии:

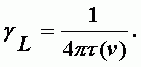(А-7)

     здесь t(n) - время жизни в возбужденном состоянии поглощающей или излучающей молекулы, зависящее от ее скорости. Обычно это устанавливается через среднюю скорость молекул и времени жизни. Из кинетической теории газов получается выражение, которое в основном соответствует квантовомеханической неадиабатической теории уширения спектральных линий давлением Андерсона (1949 г.):

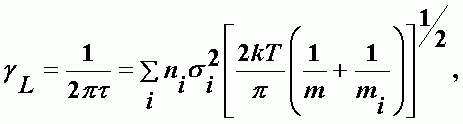(А-8)

     где n_i - концентрация молекул i - го типа; s_i - эффективное расстояние между возбужденной молекулой и молекулой i - го типа; m и m_i - массы указанных молекул.

     Для двухкомпонентной смеси полуширина линии записывается в более простой форме:

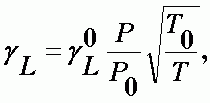(А-9)

     где g_L⁰ - полуширина линии при стандартных условиях (Р = 1 атм, Т₀ = 273⁰К). Наиболее вероятное для атмосферных газов значение g_L⁰ = 0.08 см^-1.

     Совместное действие эффектов Доплера и столкновений молекул. В атмосфере оба эффекта работают одновременно, но в нижних слоях (до 7 км) преобладает эффект столкновений, далее действие обоих эффектов оказывается одинаковым (7 … 37 км), еще выше преобладает эффект Доплера (> 40 км).

     Совместное рассмотрение двух эффектов уширения спектральных линий приводит к следующему выражению для коэффициента поглощения:

(А-10)

где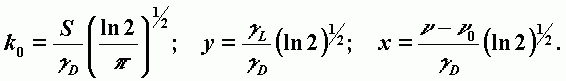

     Интенсивность спектральной линии. Записывается через коэффициент поглощения k(n):

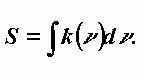(А-11)

     Квантовая механика для интенсивности отдельного перехода молекулы из состояния с индексом j в состояние, характеризуемое индексом i, дает следующее выражение:

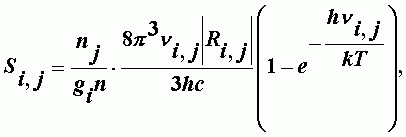(А-12)

     где n_j - концентрация молекул в нижнем состоянии; n - концентрация всех молекул; g_i - статистический вес; n_i,j - частота перехода; R_i,j² - квадрат матричного элемента дипольного момента; Т, h, k, c - абсолютная температура, постоянные Планка, Больцмана и скорость света.

     Нахождение матричных коэффициентов - сложная задача. Эти коэффициенты связаны с известными коэффициентами Эйнштейна А_i,j, характеризующими вероятности вынужденного излучения и поглощения между уровнями молекулы с индексами i и j:

(А-13)

     Для электрического дипольного излучения величины А_i,j, имеют порядок 10⁸, 10 и 1 сек^-1 для электронных, колебательных и вращательных переходов соответственно.

     Спектральная полоса поглощения. Каждому электронному состоянию соответствует сетка колебательных энергетических уровней, характеризуемых определенным значением колебательного квантового числа n. В свою очередь каждому колебательному уровню соответствует серия вращательных уровней, характеризуемых определенным значением вращательного квантового числа j.

     Из рис. А.1 следует, почему электронные и колебательные переходы в молекуле не могут наблюдаться в чистом виде. В ансамбле молекул имеем дело с их статистическим распределением по величине электронной, колебательной и вращательной энергии. При каждом электронном переходе одновременно меняются колебательная и вращательная энергии. Вся совокупность электронных переходов образует электронно-колебательно-вращательный спектр, интенсивность линий которого определяется распределением молекул по энергетическим уровням и вероятностям соответствующих переходов.

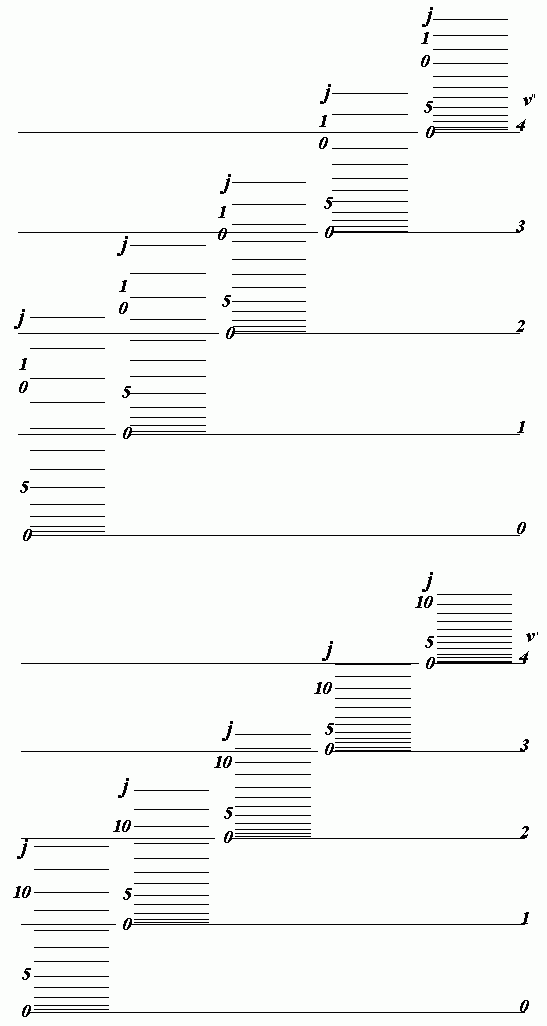Рис. A.1 - Схема колебательных и вращательных уровней двух электронных состояний молекулы (один и два штриха, что соответствует верхнему и нижнему электронным состояниям молекулы).

     Электронно-колебательно-вращательный спектр представляет собой набор полос. Каждой совокупности переходов молекулы между двумя электронными состояниями соответствует электронная полоса, состоящая из набора колебательно-вращательных полос. Высокие колебательные уровни могут перекрываться нижними уровнями соседнего более высокого электронного состояния. Это усложняет характер спектра.

     Вращательная энергия. Вращающаяся молекула рассматривается как твердое тело - жесткий волчок. Особенности вращения молекулы определяются главными моментами инерции относительно трех осей.

     Линейные молекулы. Энергия вращения:

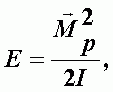(А-14)

     где M_p² - квадрат момента количества движения, I - момент инерции относительно оси вращения, перпендикулярной оси молекулы и проходящей через ее центр тяжести,

(А-15)

     h - постоянная Планка, j - вращательное квантовое число, j = 0, 1, 2, 3, …

     Квантовая энергия молекулы:

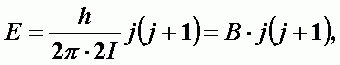(А-16)

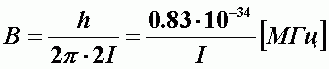- вращательная постоянная молекулы.

j	0	1	2	3	4	5	6	7	8	9	10
Ej	0	2B	6B	12B	20B	30B	42B	56B	72B	90B	110B

     Расстояние между последовательными уровнями энергии

(А-17)

     пропорционально величине j.

     Число молекул с данным j при тепловом равновесии определяется как:

(А-18)

     n₀ - число молекул в состоянии j = 0.

№ п/п	Момент инерции	Тип молекулы	Группы газов
1.	Ia = 0 Ib = Ic№ 0	Линейные молекулы	СО2, N2O, NO, CO, O2, N2, (SO2)
2.	Ia№0 Ib = Ic№ 0	Симметричный волчок	Среди атмосферных газов нет
3.	Ia = Ib = Ic№ 0	Сферический волчок	СH4
3.	Ia № Ib №Ic	Асимметричный волчок	H2O, O3, HDO

     Молекулы типа сферического волчка. Простейший тип нелинейных молекул. Уровни вращательной энергии определяются той же формулой, что и линейные молекулы. Но у них больше число степеней свободы. Распределение молекул по вращательным состояниям:

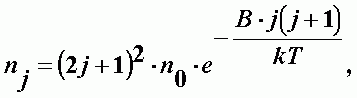(А-19)

     Молекулы типа асимметричного волчка. Для молекул типа асимметричного волчка:

(А-20)

     A, B, C - вращательные постоянные молекулы соответственно по осям.

     Асимметрия волчка:

(А-21)

     для вытянутого волчка c = - 1 ; при B=(A+C)/2 (наиболее асимметричный волчек) c = 0 ; для воды c = - 0,430.

     Спектры молекул очень сложны. Разрешены переходы Dj = 0, ±1. При этом переходам с Dj = 0, +1, -1 соответствуют Q, R, и P ветви.

     Колебательная энергия молекул. Молекула содержащая N атомов имеет 3N степеней свободы. Из них 3 приходится на поступательное движение центра тяжести молекулы, 3 или 2 - на вращательное движение. Линейные молекулы имеют 2 степени свободы вращательного движения, нелинейные молекулы - 3 степени свободы. Нелинейная молекула имеет 3N-6 степеней свободы колебательного движения и в общем случае столько же различных частот колебаний. У линейной молекулы 3N-5 степеней свободы и частот колебаний. У симметричных молекул некоторые частоты совпадают вследствие вырождения.

     Простейшей моделью колебательного движения молекулы является гармонический осциллятор. Для этой модели квантовая механика дает выражение колебательной энергии:

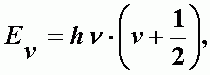(А-22)

     где 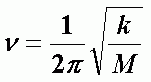- частота колебаний, n - колебательное квантовое число, n = 0, 1, 2, 3, … , k - константа квазиупругой силы, М - масса осциллятора.

     Разность энергий соседних уровней равна:

(А-23)

     Уровни энергии находятся на одинаковом расстоянии.

     Разрешены переходы Dn = ± 1 между соседними уровнями с одной и той же частотой. Для двухатомной молекулы колебательная энергия молекулы:

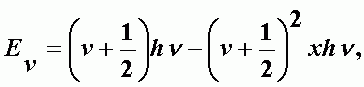(А-24)

     x - постоянная ангармоничности. Так для молекулы состоящей из разных атомов для колебательных частот n_k имеем:

(А-25)

     где n¹¹ и n¹ - колебательные квантовые числа верхнего и нижнего состояний молекулы. Например, для серии , начинающейся с нулевого уровня (n¹ = 0), получим: n_k(0, n¹¹) = n(1-x)n¹¹ - nxn¹¹², откуда следует совокупность частот колебательных переходов и, следовательно колебательно-вращательных полос:

(А-26)

     Расстояние между соседними линиями с ростом n¹¹ и частоты убывает. Линии сходятся к границе соответствующей диссоциации молекулы.

     Взаимодействие колебаний и вращения молекулы учитывается с помощью вращательной постоянной, являющейся функцией колебательного квантового числа n:

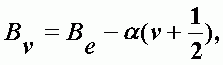(А-27)

     B_e - вращательная постоянная неколеблющейся молекулы; a - постоянная, отношение которой к B_e не превышает нескольких сотых. B_e линейно убывает с ростом квантового числа. Энергия перехода между двумя уровнями:

(А-28)

     Разность E¹¹-E¹=n₀₀ определяет частоту чисто колебательного перехода (частоту нулевой линии) j¹¹ = j¹ = 0. Переход, соответствующий нулевой линии запрещен. Положение этой линии определяется расчетным путем. Переходы, определяемые разностью энергий уровней, порождают следующие ветви полос колебательно-вращательного спектра:

     при Dj¹¹ = j¹ = + 1 переходы образуют R ветвь,

     при Dj¹¹ = j¹ = + 0 переходы образуют Q ветвь,

     при Dj¹¹ = j¹ = - 1 переходы образуют P ветвь.

    Для Q ветви получаем частоты переходов

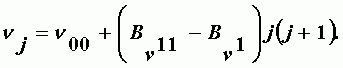(А-29)

    Так как разность B_n¹¹-B_n¹ очень мала, линии Q ветви расположены очень близко. ИК-полосы делят на параллельные и перпендикулярные по совпадению или перпендикулярностью направления дипольного момента с направлением оси симметрии молекулы. Перпендикулярная структура создает в центре полосы максимум поглощения. Параллельная - минимум (отсутствие Q ветви).

    Линейные молекулы. Имеются как параллельные, так и последовательные молекулы. Спектры имеют ранее описанную структуру.

    Сферический волчок. Положение вращательных линий в колебательно-вращательной полосе имеет тот же характер, что и для линейных молекул. Полосы поглощения состоят из трех ветвей. Взаимодействие колебательного и вращательного движений обуславливает расщепление трижды вырожденных колебаний.

    Асимметричный волчок. Молекулы имеют сложные колебательные и колебательно-вращательные спектры. Сложный выбор разрешенных квантовых чисел с учетом трех постоянных, асимметричности, ангармоничности колебаний, центробежного растяжения, резонансного возмущения уровней энергий, влияния сил Кориолиса. Могут возникать параллельные и последовательные полосы.