Кинематика образования огранки отверстий
Малышко И.А., Рожков А.С. (ДонНТУ, г.Донецк, Украина)
In this work discover problems dealing with the
research of facet kinematics of holes in cutting process by axis tools.
При обработке отверстий
многозубыми развертками наблюдается огранка отверстий, которая отрицательно
сказывается на эксплуатационных свойствах машин. Такая же проблема характерна
и для однозубых разверток. Поэтому целью данной работы
является разработка математической модели образования огранки отверстий для
однозубой развертки.
Колебаниями,
порождающими огранку отверстий, могут быть только
колебания, изменяющие сумму проекции сил резания на координатные оси g и e (рис. 1). Такими колебаниями
являются радиальные, которые направлены по координатам g и e.
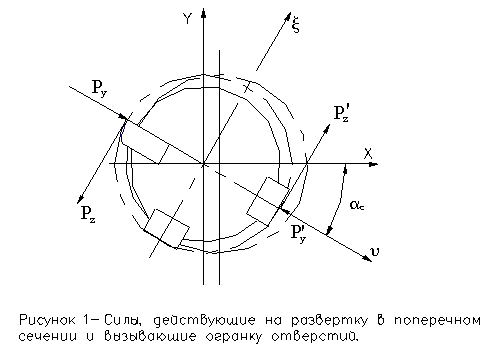
При крутильных колебаниях
сумма приращений сил резания сводится к паре сил относительно оси инструмента,
а равнодействующая этой пары в любой момент времени равна нулю, значит,
крутильные колебания не оказывают влияния на огранку отверстий. Аналогично
можно сказать и в отношении осевых колебаний развертки.
Определение взаимного
влияния крутильных колебаний на осевые и радиальные является важным моментом
для анализа динамической системы станка. Допустимо предположить, что при
развертывании крутильные колебания от оси резания не оказывают влияния на
радиальные и осевые, а радиальные колебания не влияют на осевые. В дальнейшем
радиальные колебания будем рассматривать как независимые от осевых и
крутильных.
Для составления уравнения,
характеризующего траекторию движения вершины зуба при вынужденных колебаниях, а
следовательно, и для определения формы поперечного сечения обработанного
отверстия достаточно знать уравнение движения центра развертки.
При определении уравнения движения
центра рассмотрим схему радиальных колебаний развертки (рис. 1) по координатам 
и 
. Для однозубой развертки сумма проекций от приращения
радиальных сил на ось g-SDPg приближается к SDPe.
Перемещение развертки по
координатам 
и 
в статическом положении
можно представить:
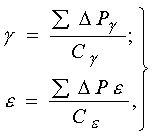(1)
где Cg = Ce -
радиальная жесткость развертки по осям 
и 
соответственно.
Преобразуем уравнение (1) к
виду:
(2)
Для определения координат
перемещений центра развертки систему уравнений (2) возведем в квадрат и
просуммируем:
. (3)
Так как перемещения по осям 
и 
различны ( 
), а радиальная
жесткость 
, то:
,
откуда получим:
.
Выражение (4) является
уравнением эллипса. Можно предположить, что если сумма проекций радиальных сил
при колебательном движении на ось 
не равна сумме
проекций сил на ось 
, то траектория, которую опишет центр развертки, будет иметь
форму эллипса.
Для определения траектории,
описываемой вершиной зуба развертки, кроме уравнения движения центра,
необходимо знать также и его направление.
При наличии внешнего
воздействия и отсутствия сил демпфирования или при малой их величине, сила
резания отстает от изменения толщины среза, в результате чего вершина зуба
инструмента будет двигаться в направлении противоположном вращению инструмента.
Так как зуб развертки и ее центр связаны жесткой кинематической связью,
направление движения центра будет определяться направлением движения вершины
зуба, полученным при врезании развертки.
После образования среза на
поверхности резания его норма ввиду наличия обратной связи с замкнутой динамической
системой СПИД будет в свою очередь оказывать влияние на территорию движения
центра развертки.
По мере входа зуба развертки
в обработанное отверстие силы упруго-пластического
контакта на калибрующей ленточке увеличиваются. Это должно привести к опережению
роста силы резания по сравнению с приращением толщины среза, а следовательно, к
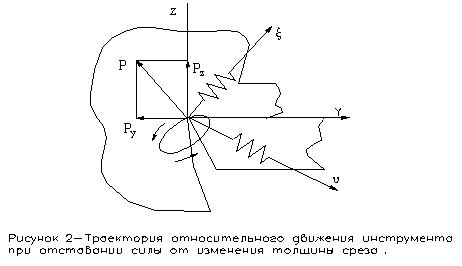
движению вершины зуба инструмента в направлении его вращения (рис. 2).
Анализ процесса
развертывания показал, что в большинстве случаев наблюдается односторонние
врезание зуба развертки в предварительно обработанное отверстие, что ведет к
его разбиванию, а следовательно, и к уменьшению сил демпфирования, какими являются
силы упругопластического контакта, действующего на вспомогательную режущую
кромку, в результате чего они становятся недостаточными для изменения направления
движения центра развертки.
Рисунок
2- Траектория относительного движения инструмента при отставании силы от
изменения толщины среза.
Уравнение колебательного
движения центра, когда его направление является противоположным направлению
вращения развертки относительно неподвижной системы координат 
(рис. 3), имеющей
общее начало с геометрической осью предварительно обработанного отверстия,
имеет вид:
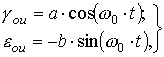(5)
где 
,
- координаты вершины лезвия инструмента по осям 
и 
соответственно;
, 
– амплитуда радиальных поперечных колебаний центра развертки;
- круговая частота
колебаний центра.
Уравнение (5) можно представить в виде:
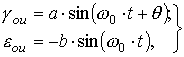(6)
где 
- сдвиг фаз колебаний.
Для определения траектории движения зуба развертки примем допущение, что период колебаний центра определяется временем одного полного оборота развертки вокруг своей оси.
Так как развертка, кроме колебательного движения центра,
совершает еще и вращательное движение, имеет смысл ввести подвижную систему
координат 
, которая имеет общее начало с центром развертки 
(рис. 3). Для
установления связи между системой координат 
и системой 
введем неподвижную
вспомогательную систему координат 
.
Разобьем поперечное сечение обрабатываемого отверстия на
элементарные секторы в подвижной системе координат 
.Тогда положение зуба развертки в подвижной системе координат
определится:
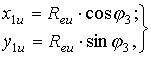(7)
где 
- радиус зуба развертки при эксцентричном расположении относительно
оси отверстия;
- величина эксцентриситета зуба развертки в секторе 
;
- величина эксцентриситета зуба развертки в секторе 
и равная 
.
Формулы перехода от подвижной
системы координат 
к неподвижной (вспомогательной)
имеют вид:
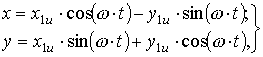(8)
где 
- круговая частота вращательного движения разверстки,
равная суммарной частоте вращения заготовки и инструмента:
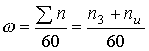. (9)
Подставив
значение 
и 
в формулы
преобразования координат (8), получим уравнение движения зуба развертки относительно
неподвижной (вспомогательной) системы
координат 
:
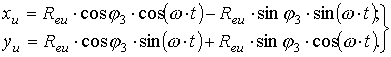(10)
Уравнение
движения зуба развертки относительно неподвижной системы координат 
:
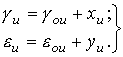(11)
Подставив
значение координат 
в уравнение (11), получим:
(12)
Преобразуем выражение (12):
(13)
При принятом законе движения вершины K уравнение поверхности обработанного отверстия получены в виде:
(14)
где m - отношение частоты
поперечных колебаний развертки и частоте вращения заготовки
.
Величина
при обработке
отверстия является углом поворота заготовки.
Величина m для однозубой развертки физически представляет число врезаний и выходов инструмента за один оборот заготовки или количество граней. В результате круговая цилиндрическая поверхность обработанного отверстия превращается в граненую (со впадинами и выступами).
Число врезаний m может быть не целым числом, т.е.
,
где 
- целое число врезаний инструмента в материал заготовки за
один ее оборот относительно инструмента;
-врезание, выходящее за один оборот заготовки ( 
).
Величина
является величиной
сдвига фаз колебаний
.
Таким образом, получим уравнение, характеризующие закон движения зуба развертки а плоскости, перпендикулярной ее оси, и одновременно определяющее траекторию движения зуба в параметрическом виде:
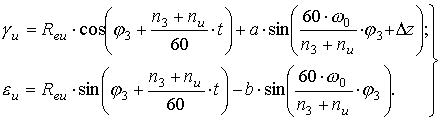(15)
Уравнение движения зуба развертки в полярной системе координат:
а) радиус-вектор
; (16)
б) полярный угол
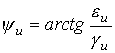. (17)
Величину огранки отверстия можно определить зависимостью:
,
где 
- радиус описанной окружности, равный максимальному радиусу
кривой, описывают зубом развертки;
-радиус вписанной окружности, равный минимальному радиусу
кривой, описываемой зубьями развертки.
Учитывая допущение, что период колебаний центра определяется временем одного полного оборота развертки вокруг своей оси, т.е.:
, (18)
то, подставив значение периода одного колебания центра развертки:
,
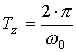в
выражении (18), получим значение элементарного времени t одного оборота развертки вокруг своей
оси
.
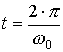Выражение (15) примет вид:
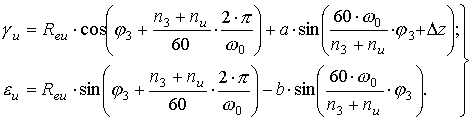(20)
Окончательно
с учетом значения 
и получим:
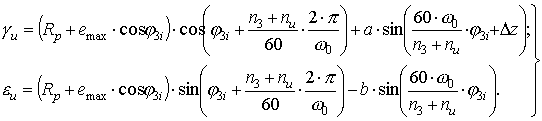
Таким образом, на основании
разработанной математической модели образования огранки отверстий для однозубой
развертки получено выражение, которое позволяет определить траекторию
движения вершины зуба развертки,
а следовательно и определить оптимальные конструктивные параметры
развертки.
Список литературы: 1. Уткин Н.Ф. Обработка глубоких
отверстий.–Л.:Машиностроение,1988.-298с. 2. Троицкий Н.Д. Глубокое сверление.-Л.:Машиностроение,1971.-176с.