Как известно, повышение надежности работы электрической системы неразрывно связано с повышением эффективности управления ее режимами. Автоматическое управление режимами работы электрической системы является иерархической системой и осуществляется согласованными действиями персонала разных уровней управления. Для высших по ступени управления уровней характерно разделение функций персонала по группам технологических задач. Например, ЦДС включает в своем составе персонал по расчетам режимов, по оптимизации режимов и оперативный персонал. В службе релейной защиты часть персонала выполняет расчеты по проектированию и анализу работы релейных защит. Информационное и прикладное программное обеспечение также носит позадачный и функциональный характер (расчет токов КЗ, расчет установившегося режима, оптимизация режима и т.д.). Расчетные модели в этих программах обычно охватывают всю энергосистему с последующей коррекцией ветвей и узлов для учета различных режимов. Следует также отметить, что основные средства управления расположены в нижнем звене на уровне электри-ческих станций, систем электроснабжения, подстанций.

Деление единой энергосистемы СССР на объединенные энергосистемы отдельных стран СНГ из-за распада СССР внесло дополнительные проблемы в процесс управления, среди которых можно отметить следующие:

- не оптимальная структура электрических станций (отсутствие ГАЭС и др. электрических станций, которые предназначены для покрытия пиковых нагрузок);

- необходимость создания оптимальных режимов работы в условиях новой конфигурации электрической системы;

- незначительное число электрических станций, работающих на местном топливе.

В связи с переходом на рыночные отношения в энергетике Украины произошли структурные изменения в энергосистемах Украины с использованием различных форм собственности.

В отмеченных условиях роль автоматизированной системы управления локальными объектами возрастает, в том числе и с целью получения максимальной прибыли.

В таких условиях функционирование электрической системы, как никогда раньше, зависит от качества работы оперативного персонала. Общеизвестной является необходимость существенного улучшения взаимодействия персонала со средствами обработки информации, особенно это, касается динамических режимов когда в стрессовых ситуациях необходима обработка значительных объемов информации

Для эффективной информационной поддержи решений персонала локальных объектов электрической системы необходимо выполнять анализ технологических задач, являющихся совокупностью функциональных. Персонал должен оперативно оценить эффективность принятого решения. Такая оценка возможна только при использовании моделирования, позволяющего оперативно формировать адаптируемые к различным вариантам исследований модели.

В [1,2] других приведены результаты анализа принципов построения и особенностей полной и основных упрощенных моделей переходных и установившихся процессов в сложных электроэнергетических системах. Однако при анализе не в полной мере рассматриваются вопросы моделирования на основе современных информационных технологий. Анализ ряда комплексов программ, которые в различной степени позволяют моделировать установившиеся режимы работы, электромагнитные и электромеханические переходные процессы, позволяет сделать вывод, что вопросам создания единой инфологической модели объекта моделирования уделяется недостаточно внимания.

В АСДУ на уровне энергосистемы используется программное обеспечение, четко определяющее специфику математических моделей элементов системы используемых для решения задач в соответствующей службе. При этом составляется математическая модель, описывающая всю систему в целом. Как результат имеется система дифференциально-алгебраических уравнений описывающих режимы всей системы в целом. При этом возможно использование эквивалентирования отдельных участков системы. Этот подход не позволяет оперативно создавать многофункциональные (адаптивные) модели для решения большого круга задач.

При моделировании технологических задач используются математические модели элементов, полученные после определенных этапов представления элемента электрической системы и преобразования информации о свойствах элемента, выполняемых другими программами или вручную. Эти математические модели обеспечивают реализацию логической схемы конкретной задачи. Этот подход, исчерпавший свои возможности, является причиной жестких математических моделей и тормозом повышения эффективности математического моделирования.

Комплексы программ, применяемые сегодня, используют внешние логические модели согласно современным информационным технологиям, что приводит к определенным трудностям взаимодействия пользователя с ПЭВМ при проведении многовариантных исследований. Это обусловлено объективными факторами.

Применение ПЭВМ развивалось по двум направлениям использования. Первое направление - применение вычислительной техники для выполнения численных расчетов, которые слишком долго или вообще невозможно производить вручную. Становление этого направления способствовало интенсификации методов численного решения сложных математических задач, развитию класса языков программирования, ориентированных на удобную запись численных алгоритмов. Второе направление - это использование средств вычислительной техники в автоматизированных информационных системах. Второе направление возникло несколько позже первого. Это связано с тем, что на заре вычислительной техники компьютеры обладали ограниченными возможностями в части памяти (внешней и главным образом ОЗУ), что было не очень существенно для чисто численных расчетов. Даже если программа должна обработать большой объем информации, при программировании можно продумать расположение этой информации во внешней памяти, чтобы программа работала как можно быстрее.

Для повышения эффективности управления локальными объектами электрической системы (электрические станции, системы электроснабжения, линии связи, участки сети, подстанции) на основе математического моделирования, необходимо:

- использование методов автоматического формирования адаптивных моделей локальных объектов при использовании эквивалентов примыкающих локальных объектов, концепция которых изложена в [3];

- создание многофункциональных адаптируемых моделей, что обеспечит интеграцию различных задач при моделировании для принятия решения.

- упрощение математической модели без принятия дополнительных допущений, снижающих точность моделирования. Как известно, усложнение математической модели сопровождается повышением требований достоверности исходных данных. В новых условиях функционирования локальных объектов электрической системы усложнятся формы получения информации от смежных объектов, вплоть до заключения соответствующих договоров.

Целью настоящей статьи является рассмотрение моделирования режимов локальных объектов на единой информационной модели в рамках автоматизированной система управления режимами электрических систем [4].

Предлагается математическая электрической системы, основанная не на общей системе уравнений для всей системы в целом, а на совокупности элементов подсистемы: генераторы, узлы нагрузки, сеть, для которых рассматриваются системы уравнений. При этом упрощается не только решение технологической задачи без принятия каких-либо допущений, снижающих точность, но создаются условия для эффективного использования автоматически построенных с помощью графического интерфейса математических моделей объектов электрической системы. Это позволит расширить круг решаемых задач, которые относятся к задачам оперативного протиаварийного управления.

Исходный установившийся режим работы электрической сети описывается системой алгебраических уравнений, полученных с помощью метода узловых напряжений.

При исследовании переходных режимов используется математическая модель следующего вида:

- пассивная часть электрической системы описывается системой уравнений следующего вида в матричной форме

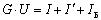
где G – матрица проводимостей; U – вектор мгновенных значений напряжений в узлах; I – вектор мгновенных значений токов в узлах, определяемый решением дифференциальных уравнений, описывающих генераторы или двигатели, подключенные в узлах; I' – вектор произведений производных токов на постоянные времени, определяемый как отношение приращения тока за интервал к длительности интервала; IБ – вектор токов, зависящий от наличия связи с балансирующим узлом (составляющие определяются по правилу: равна 0, если узел не имеет связи с балансирующим узлом, в противном случае равен произведению проводимости на напряжения балансирующего узла).

При этом задающие токи в узлах находят на основании решения систем уравнений, описывающие переходные процессы в генераторах, двигателях, обобщенной нагрузке питающихся от рассматриваемых узлов. Производные тока можно определить так:

тогда имеем

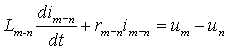
или

где мгновенное значение тока в ветви связывающей узлы m и n ;

На основании первого закона Кирхгофа для каждого узла можно записать:

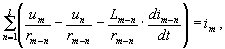
где im- мгновенное значение задающего тока в узле m (генераторы, на-грузка); l - число узлов в схеме.
Введем обозначения:

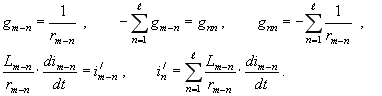
С учетом обозначений для каждой фазы это уравнение было записано в матричном виде (1). Уравнения решаются для каждой фазы отдельно, что позволяет выполнить расчет переходных режимов при наличии несимметрии в сети.

Для определения мгновенных значений тока генератора используют либо полные уравнения Парка-Горева для генераторов, расположенных вблизи места возмущения [5]. Либо упрощенная модель [6] для генераторов, удаленных от места возмущения :

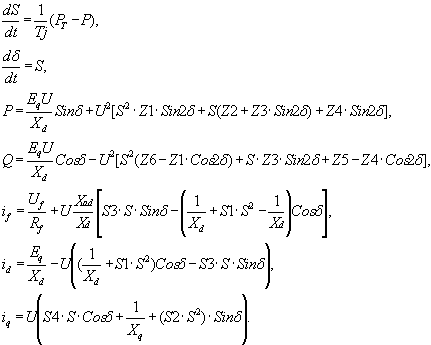
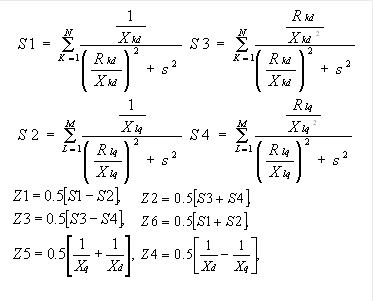
где Хd, Xq - синхронные индуктивные сопротивления генератора; Rkd, Xkd , Rlq, Xlq - параметры k - го по оси d и l - го по. оси q демпферных контуров известной схемы замещения с вынесенным контуром намагничивания; N, M - число демпферных контуров с постоянными параметрами.

Система уравнений дополняется дифференциальными уравнениями, описывающими работу систем автоматического регулирования скорости агрегата и возбуждения генератора.

Кроме того, система уравнений дополняется неравенствами, реализующими ограничения по току статора и возбуждения для генераторов и по реактивной мощности для статических тиристорных компенсаторов. После ввода возмущения выполняется переформирование матрицы узловых проводимостей, так как генераторные ветви, которые ранее были заданы мощностями, теперь необходимо представить в виде блоков систем дифференциальных уравнений. На каждом шаге численного интегрирования рассчитывается токи в узлах с генераторами и двигателями, затем производные токов, затем решением уравнения напряжение узлов, токи в ветвях, затем снова выполняется интегрирование дифференциальных уравнений. Число блоков уравнения для описания генераторов и систем их регулирования столько, сколько, сколько имеется в исследуемой схеме генераторных ветвей.

Для анализа статической устойчивости реализован метод утяжеления режима. В качестве напряжений генераторных узлов принимаются ЭДС генераторов. Активные мощности этих ветвей равны мощностям турбин. Автоматически вводятся возмущения в схему путем изменения углов ЭДС на небольшую величину, равную 5% от значения угла исходного установившегося режима. Выполняется переформирование матрицы узловых проводимостей, так как генераторные ветви, которые ранее были заданы мощностями, теперь необходимо представить ЭДС и объединить с примыкающими ветвями, а также исключить генераторные узлы. После этого выполняется численное интегрирование уравнений для всех генераторных ветвей. По изменению угла делается вывод о статической устойчивости режима системы.

При моделировании сложных систем, включающих в себя синхронные машины, часто бывает необходимо предусматривать те или иные изменения первичной схемы во время переходного процесса. Обычно следует предусматривать отключение отдельных машин, элементов нагрузки, линий и т. п. При последующих операциях, таких как повторное включение, для правильного отображения процессов в отключенных машинах переменного тока использованы схемы моделирования в виде "источников тока" [6].

Список литературы

1. Баринов В.А., Совалов С.А. Режимы энергосистем: Методы анализа и управления. – М.: Энергоатомиздат, 1990. – 440 с.

2. Математическое моделирование установившихся режимов электрических систем переменно-постоянного тока / Г.Н. Лысяк, В.Н. Стряпан, А.В. Данилюк. – К.: УМК ВО, 1990. 104 с.

3. Заболотный И.П., Павлюков В.А. Метод оперативного формирования моделей электрических систем // Вісник Національного університету "Львівська політехніка". – Львів: Львівська політехніка, №403. – 2000. – С. 56-62.

4. Заболотный И.П., Павлюков В.А. Применение компьютерных технологий для управления электрическими системами // Технічна електродинаміка, спеціальний випуск, К.: 1998. – с.90-99.

5. Применение аналоговых вычислительных машин в энергетических системах / Под. ред. Н.И. Соколова. - М.: Энергия, 1970. – 400 с.

6. Заболотный И.П., Диа Ибрагим. Разработка минимальной сложности математической модели генератора для анализа длительных переходных процессов в энергосистемах // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 2, Донецк: ДонГТУ, 1998. – С. 181-188.