КОНСТРУИРОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
ЛИНЕЙНЫХ САУ ИЗ УСЛОВИЙ
МОДУЛЬНОГО ОПТИМУМА
Толочко О.И., Коцегуб П.Х., Губарь Ю.В., Федоряк Р.В.
Донецкий государственный технический университет
Olga@pandora.kita.donntu.ru
Збiрник наукових праць ДонДТУ.Серiя “Електротехнiка i енергетика”, випуск 17: - Донецьк:
ДонДТУ, 2000. - с.24-30.
This article proposes the principles of automatic control systems synthesis with help
of choosing of characteristic polynomial coefficients with double proportion method, while
coefficients of an input polynomial – from conditions of absolute value optimum. Analytic
expressions were brought out and coefficients numerical values were figured. This work includes
an analysis of zeros and poles arrangement and transient process quality. This article gives an
example, which confirms the effec-tiveness of a proposed synthesis method for doublemass
electromechanical object’s modal control system.
Один из способов синтеза линейных систем автоматического управления (САУ), в частности систем
модального управления (СМУ), заключается в размещении полюсов системы в выбранных позициях.
Для этого используют стандартные формы характеристических полиномов, соответствующие
определенным критериям оптимизации. Одним из таких критериев может быть модульный оптимум (МО),
обеспечивающий постоянство модуля амплитудно-частотной характеристики (АЧХ) замкнутой системы в
возможно большем диапазоне частот.
Для системы с передаточной функцией (ПФ)
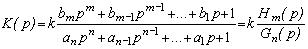 ,
,

и выражением для квадрата модуля АЧХ
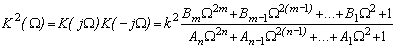 ,
,
где
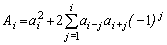 ,
, 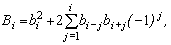 ,
,
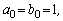 ,
,
условия оптимизации по модульному оптимуму имеют вид [1]:
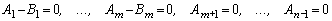 ,
,
При m=0 система (4) после подстановки в нее выражений (3) содержит n-1 уравнение с
n неизвестными, т.е. один из коэффициентов ai должен быть выбран до решения системы
уравнений (4).
В теории линейных электрических цепей таким коэффициентом обычно является
 ,
,
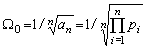 ,
,
где
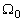 –среднегеометрический корень характеристического полинома,
–среднегеометрический корень характеристического полинома,
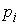 –полюса ПФ (1).
–полюса ПФ (1).
Нормируя (1) по частоте  , получаем
, получаем
 ,
,
где
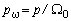 ,
,
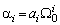 ,
,
 .
.
Система уравнений (4) для ПФ (6) при m=0 имеет вид:
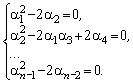
Решение этой системы относительно коэффициентов ai
при m=0 дает коэффициенты фильтра Баттерворта [2], имеющего максимально плоскую АЧХ в полосе
пропускания и характеризующегося равномерным распределением полюсов на окружности радиуса
 .В литературе обычно приводятся с разной степенью точ-ности приближенные
значения коэффициентов этого фильтра. Для полиномов Баттерворта второго-шестого порядков можно
определить точные выражения, позволяющие вычислить его коэффициенты с любой степенью точности
(в пределах разрядной сетки применяемой ЭВМ):
.В литературе обычно приводятся с разной степенью точ-ности приближенные
значения коэффициентов этого фильтра. Для полиномов Баттерворта второго-шестого порядков можно
определить точные выражения, позволяющие вычислить его коэффициенты с любой степенью точности
(в пределах разрядной сетки применяемой ЭВМ):
n=2 - 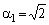 ;
;
n=3 - 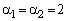 ;
;
n=4 - 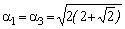 ,
,
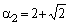 ;
;
n=5 -  ,
,
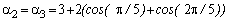 ;
;
n=6 - 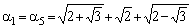 ,
,
 ,
,
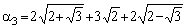 .
.
Переходные функции систем с распределением полюсов по Баттерворту при возрастании порядка
характеристического полинома становятся излишне колебательными и имеют повышенное
перерегулирование.
В процессе практического применения МО при синтезе систем подчиненного регулирования возник
несколько иной подход к формированию характеристического полинома. Постоянные времени
интегрирования контуров в этих системах выбираются последовательным решением первого уравнения
системы (4) для поли-номов 2-го, 3-го и т.д. порядков, в результате чего характеристический
полином системы с передаточной функ-цией (1) и его коэффициенты принимают вид:
 ,
,
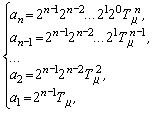
где Tm – малая не компенсируемая постоянная времени привода.
Обобщая выражения (10), можно записать:

Такой способ оптимизации в немецкой литературе называется, в отличие от модульного оптимума
(Betragsoptimum), методом двойных пропорций (Methode der Doppelverhдltnisse) [3].
Среднегеометрический корень полинома (9) в соответствии с (5) и (10) зависит от его порядка и
составляет
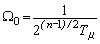 .
.
При проектировании систем модального управления выбор этой частоты не связан столь жестким
соотношением с порядком характеристического полинома. Обычно ее выбирают из условий достаточной
помехоза-щищенности и реализуемости коэффициентов модального регулятора.
Для синтеза СМУ удобно использовать стандартные полиномы, нормированные по их
среднегеометрической частоте.
Подставляя во второе уравнение системы (7) выражения (11) и (12), получим формулу для
определения коэффициентов характеристического полинома (9), пронормированного по частоте
 (см ПФ (6))
(см ПФ (6))
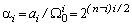 ,
, 
откуда
 .
.
Анализ выражений (13), (14) показывает, что исследуемый многочлен будет иметь симметричные
коэффициенты:
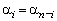 .
.
Из этого следует, что для него будет справедливо не только первое, но и последнее уравнение
системы (8):

Поэтому при n=2 и n=3 коэффициенты полинома (14) совпадают с коэффициентами фильтра Баттерворта
соответствующего порядка.
В таблице 1 представлены полиномы (9) второго-восьмого порядков, пронормированные по частоте *0
и по частоте 1/Tm:
 ,
,  ,
,
а на рис.1 – карта расположения корней характеристического полинома (14) Im(pwi)((Re(pwi))
(числами на ри-сунке обозначен порядок многочлена).
Таблица 1
Нормированные характеристические полиномы, сконструированные методом
двойных пропорций
| n=2 |
G2(pm) |
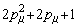 |
| n=2 |
G2(pm) |
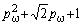 |
| n=3 |
G3(pm) |
 |
| n=3 |
G3(pm) |
 |
| n=4 |
G4(pm) |
 |
| n=4 |
G4(pm) |
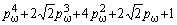 |
| n=5 |
G5(pm) |
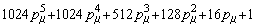 |
| n=5 |
G5(pm) |
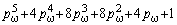 |
| n=6 |
G6(pm) |
 |
| n=6 |
G6(pm) |
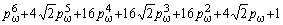 |
| n=7 |
G7(pm) |
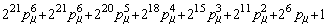 |
| n=7 |
G7(pm) |
 |
| n=8 |
G8(pm) |
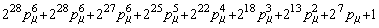 |
| n=8 |
G8(pm) |
 |
Из рис.1 видно, что при оптимизации систем методом двойных пропорций максимальный угол
между действительной осью и векторами полюсов при повышении порядка полинома остается практически
постоянным в отличие от полюсов фильтра Баттерворта, для которых этот угол все время
увеличивается. Анализ чис-ленных значений корней характеристического уравнения показывает, что
минимальные коэффициенты демп-фирования колебательных звеньев, образованных
комплексно-сопряженными парами полюсов, составляют для второго и четвертого порядков 0.707, для
третьего порядка – 0.5, для пятого-восьмого порядков – »0.65. До n=4 полюса располагаются на
окружности единичного радиуса, а при nі5 эта закономерность, несмотря на симметричность
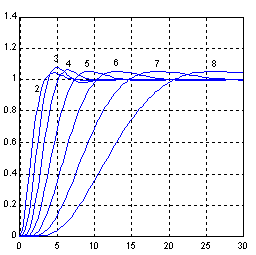
характеристического полинома, нарушается. Такое расположение полюсов, как видно из рис.2, где
изображены переходные функции h(W0t) системы с ПФ 1/Gn(pw) при рассматриваемой настройке,
обеспечивает протекание переходных процессов с невысоким перерегулированием и с малой
колебательностью, что особенно важно для электромеханических систем с упругими кинематическими
передачами.

|
|
Рисунок 1 |
Рисунок 2 |
Недостатком оптимизации методом двойных пропорций является существенное снижение быстродействия
при повышении порядка системы. Устранить его можно применением принципа комбинированного
управления по задающему воздействию (системы с упреждающей коррекцией). Наиболее просто
комбинированное управление реализуется в системах, работающих с задающими устройствами [4,5].
Используя параллельные корректирующие сигналы по производным от управляющего воздействия, удается
сформировать полином воз-действия 1-го, 2-го, 3-го и даже 4-го порядков передаточной функции
замкнутой системы и при определенных значениях его коэффициентов обеспечить существенное
увеличение быстродействия без увеличения перерегулирования.
Как показывает опыт синтеза комбинированных систем [6], хорошие результаты получаются при
выборе коэффициентов знаменателя ai передаточной функции (6) замкнутой системы методом двойных
пропорций (13), а числителя – решением системы уравнений, составленной из m первых условий
модульного оптимума, относительно коэффициентов bi.Применительно к нормированной ПФ (6)
при 0 < m < n эта система уравнений будет иметь вид
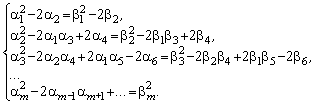
Из сопоставления систем уравнений (16) и (18) видно, что при m=n-1 коэффициент bn-1, а
при m=1 коэф-фициент b1 оказываются тождественно равными нулю. Таким образом, порядок полинома
воздействия при данном способе оптимизации должен быть не менее 2 и не более, чем n-2. Отсюда
еще раз вытекает, что систе-мы с рассматриваемыми характеристическими полиномами до 3-го порядка
включительно соответствуют тре-бованиям МО при m=0 и, следовательно, с этой точки зрения, не
нуждаются в упреждающей коррекции. В со-ответствии с приведенными рассуждениями порядки полиномов
передаточной функции замкнутой системы для предлагаемой методики синтеза должны находиться в
диапазоне
 ,
,
 .
.
Полиномы воздействия Hm(pw) с коэффициентами bi, рассчитанными по этой методике для систем
четвёртого-шестого порядков приведены в таблице 2.
Таблица 2
Нормированные полиномы воздействия, сконструированные из условий МО
| n=4 |
H2(pw) |
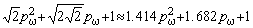 |
| n=5 |
H2(pw) |
 |
| n=5 |
H3(pw) |
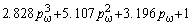 |
| n=6 |
H2(pw) |
 |
| n=6 |
H3(pw) |
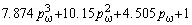 |
| n=6 |
H4(pw) |
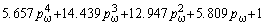 |
Следует отметить, что при использовании в знаменателе ПФ (6) полинома Баттерворта все
коэффициенты bi, выбираемые из условий (18), окажутся тождественно равными нулю.
Эффективность комбинированного управления с выбором коэффициентов характеристического
полинома методом двойных пропорций, а параметров полинома воздействия по МО демонстрируют
переходные функ-ции h(W0t), приведенные на рис.3, где для сравнения, кроме графиков,
соответствующих вышеизложенной ме-тодике синтеза, приведены переходные функции фильтра
Баттерворта (помечены буквой “Б”).
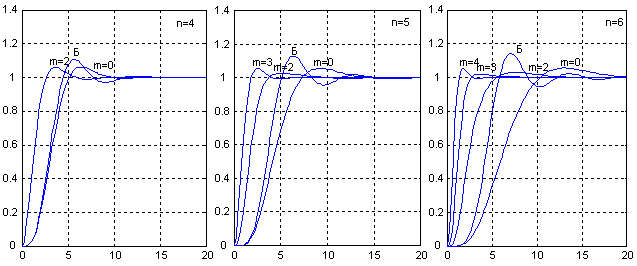
Рисунок 3
Графики подтверждают, что комбинированное управление при предлагаемой методике конструирования
передаточной функции позволяет существенно повысить быстродействие системы без повышения ее
колеба-тельности. Эффект упреждающей коррекции повышается с увеличением порядков
характеристического поли-нома и полинома воздействия.
Небезынтересно посмотреть на карты расположения нормированных нулей (о) и полюсов (х) системы,
приведенные на рис.4 (числами обозначен порядок числителя ПФ), из которых видно, что при данной
методике синтеза нули осуществляют последовательную приближенную компенсацию полюсов в порядке
возрастания их мнимых частей.
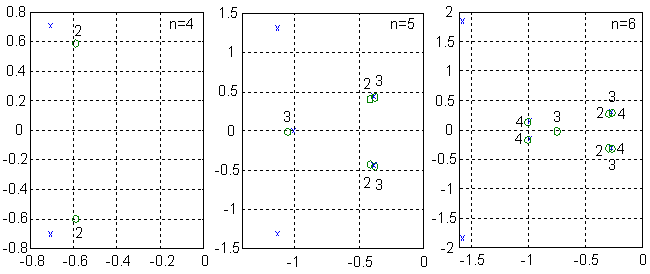
Рисунок 4
Проиллюстрируем целесообразность применения вышеизложенной методики синтеза на примере
астатической системы модального управления двухмассовым электромеханическим объектом (ДЕМО)
с задатчиком интенсивности (ЗИ) и упреждающей коррекцией. Структурная схема САУ в относительных
единицах (о.е.) изо-бражена на рис.5, где обозначены:
ТП – тиристорный преобразователь;
И-РС – интегральный регулятор скорости;
w1, w2, w0 – угловые скорости двигателя, механизма и скорость идеального холостого хода
двигателя;
wз, wзи – скачкообразный и линейный сигналы задания на скорость;
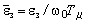 ;
;
eз – сигнал задания на ускорение;
I, Iкз – ток якоря и ток короткого замыкания якорной цепи ТП-Д;
Mу, Mкз – упругий момент кинематической передачи и момент короткого замыкания двигателя.
Параметры механизма и кинематической передачи приведены к валу двигателя.

Рисунок 5
На рис.6 представлены графики переходных процессов в рассматриваемой системе при разгоне от
ЗИ и при набросе нагрузки. На графиках а) и б) коэффициенты модального регулятора
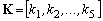 и постоянная времени И-РС Ti формируют характеристический полином с коэффициентами, соответствующими методу
двойных пропорций, а на графике в) – модульному оптимуму (т.е характеристический полином
представляет собой полином Баттерворта). На графиках а) и в) коэффициенты параллельных
корректирующих связей ЗИ рав-ны нулю, а на графике б) они выбраны из условий МО:
и постоянная времени И-РС Ti формируют характеристический полином с коэффициентами, соответствующими методу
двойных пропорций, а на графике в) – модульному оптимуму (т.е характеристический полином
представляет собой полином Баттерворта). На графиках а) и в) коэффициенты параллельных
корректирующих связей ЗИ рав-ны нулю, а на графике б) они выбраны из условий МО:
 ,
, 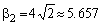 (см. таблицу 2 при n=6, m=2).
(см. таблицу 2 при n=6, m=2).
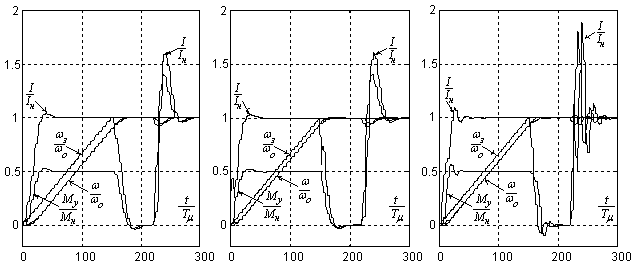
Рисунок 6
Поскольку скорости первой и второй масс w1 и w2 в приведенном масштабе на графиках практически
сливаются, они обозначены на рисунках как один сигнал w.
Переходные процессы получены при следующих параметрах:
 – электромеханические постоянные времени первой и второй масс;
– электромеханические постоянные времени первой и второй масс;
 – электромагнитная постоянная времени якорной цепи и постоянная времени упругих колебаний
двухмассовой системы;
– электромагнитная постоянная времени якорной цепи и постоянная времени упругих колебаний
двухмассовой системы;
 .
.
Из графиков рис.6 видно, что использование в характеристическом полиноме исследуемой СМУ
коэффициентов Баттерворта (в) приводит к излишней колебательности тока якоря и упругого момента,
особенно при набросе нагрузки, что крайне нежелательно. При выборе коэффициентов знаменателя
ПФ замкнутой САУ ме-тодом двойных пропорций (а,б) переходные процессы становятся менее
колебательными, быстрее затухают и имеют меньшие значения перерегулирований по току и упругому
моменту. Применение упреждающей коррек-ции, формирующей в ПФ полином воздействия второго порядка
(б), позволяет повысить быстродействие сис-темы при отработке линейно возрастающего управляющего
воздействия без увеличения перерегулирования.
Выводы
- Коэффициенты характеристического полинома, полученные из условий модульного оптимума
(Betragsoptimum) при нулевом порядке полинома воздействия, совпадают с коэффициентами фильтра
Баттерворта. Переходные процессы в такой системе при повышении ее порядка оказываются излишне
колебательными.
- При упрощенной оптимизации по МО, которую можно назвать методом двойных пропорций
(Methode der Doppelverhдltnisse), переходные процессы имеют небольшое перерегулирование (до 8%)
и низкую колебательность, однако при повышении порядка системы значительно снижается ее
быстродействие.
- Оптимизация по МО и методом двойных пропорций при порядке характеристического полинома
от 1 до 3 включительно дает одинаковые результаты.
- Повысить быстродействие систем с характеристическим полиномом, настроенным методом двойных
пропорций, без повышения перерегулирования можно применением принципа комбинированного управления
с выбором коэффициентов полинома воздействия из условий МО.
- Эффект от комбинированного управления повышается с увеличением порядков характеристического
полинома и полинома воздействия.
- Приведенные в таблицах 1,2 нормированные многочлены можно использовать в качестве стандартных
полиномов при синтезе обычных и комбинированных систем модального управления.
- Применение метода двойных пропорций при конструировании характеристического полинома
астатической системы модального управления двухмассовым электромеханическим объектом является
более предпочтительным, чем применение характеристического полинома с коэффициентами Баттерворта.
Литература
- Коцегуб П.Х., Толочко О.И. Оптимизация систем управления по модулю амплитудно-частотной
характе-ристики. - Изв. вузов, Электромеханика, 1977, №6, с.679-684.
- Айзинов М.М. Анализ и синтез линейных радиотехнических цепей в переходном режиме. - Л.:
“Энергия” 1968. - 376с.
- Vogel J. Electrische Antriebstechnik / von Vogel J. u.a. - Heidelberg: Huthig Buch Verlag,
1991. - 415S.
- А.с.764078 (СССР). Задающее устройство / Коцегуб П.Х., Толочко О.И. - Опубл. в Б.И., 1980,
№34.
- А.с. 840789 (СССР). / Фильтр для систем автоматического регулирования / Коцегуб П.Х.,
Толочко О.И. - Опубл. в Б.И., 1981, №23
- Коцегуб П.Х., Толочко О.И. Оптимизация систем управления с задатчиком интенсивности. -
Электротех-ническая промышленность. Серия “Электропривод”, 1976, вып.7(51), с.22-25.
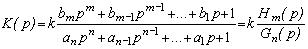 ,
,

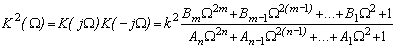 ,
,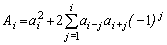 ,
, 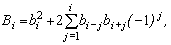 ,
,
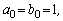 ,
,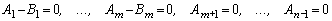 ,
, ,
,
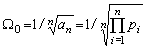 ,
,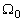 –среднегеометрический корень характеристического полинома,
–среднегеометрический корень характеристического полинома,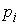 –полюса ПФ (1).
–полюса ПФ (1). , получаем
, получаем ,
,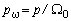 ,
,
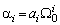 ,
,
 .
.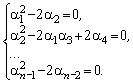
 .В литературе обычно приводятся с разной степенью точ-ности приближенные
значения коэффициентов этого фильтра. Для полиномов Баттерворта второго-шестого порядков можно
определить точные выражения, позволяющие вычислить его коэффициенты с любой степенью точности
(в пределах разрядной сетки применяемой ЭВМ):
.В литературе обычно приводятся с разной степенью точ-ности приближенные
значения коэффициентов этого фильтра. Для полиномов Баттерворта второго-шестого порядков можно
определить точные выражения, позволяющие вычислить его коэффициенты с любой степенью точности
(в пределах разрядной сетки применяемой ЭВМ):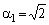 ;
;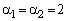 ;
;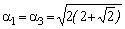 ,
,
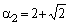 ;
; ,
,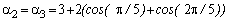 ;
;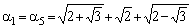 ,
,
 ,
,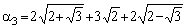 .
. ,
,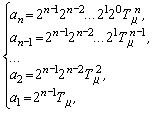

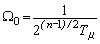 .
. (см ПФ (6))
(см ПФ (6))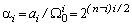 ,
, 
 .
.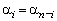 .
.
 ,
,  ,
,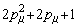
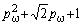



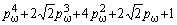
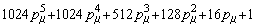
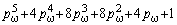

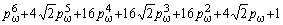
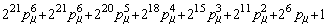

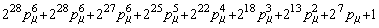



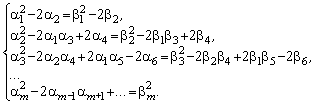
 ,
,
 .
.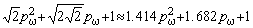

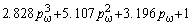

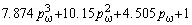
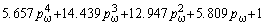


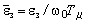 ;
;
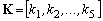 и постоянная времени И-РС Ti формируют характеристический полином с коэффициентами, соответствующими методу
двойных пропорций, а на графике в) – модульному оптимуму (т.е характеристический полином
представляет собой полином Баттерворта). На графиках а) и в) коэффициенты параллельных
корректирующих связей ЗИ рав-ны нулю, а на графике б) они выбраны из условий МО:
и постоянная времени И-РС Ti формируют характеристический полином с коэффициентами, соответствующими методу
двойных пропорций, а на графике в) – модульному оптимуму (т.е характеристический полином
представляет собой полином Баттерворта). На графиках а) и в) коэффициенты параллельных
корректирующих связей ЗИ рав-ны нулю, а на графике б) они выбраны из условий МО:
 ,
, 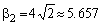 (см. таблицу 2 при n=6, m=2).
(см. таблицу 2 при n=6, m=2).
 – электромеханические постоянные времени первой и второй масс;
– электромеханические постоянные времени первой и второй масс; – электромагнитная постоянная времени якорной цепи и постоянная времени упругих колебаний
двухмассовой системы;
– электромагнитная постоянная времени якорной цепи и постоянная времени упругих колебаний
двухмассовой системы; .
.