В настоящее время прослеживается тенденция сближения методов синтеза систем подчиненного
регулирования (СПР) и систем модального управления (СМУ).
В [1] рассмотрен принцип конструирования характеристического полинома (ХП) в СПР при
оптимизации их методом двойных пропорций

и выполнено нормирование этих полиномов по среднегеометрическому корню (СГК)
 ,
,
что привело к возможности использовать их в качестве стандартных форм при синтезе СМУ.
В формулах (1) и (2) обозначены:
Tm – малая некомпенсируемая постоянная времени привода;
 - относительный оператор Лапласа;
- относительный оператор Лапласа;
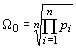 - СГК, или характеристическая частота полинома.
- СГК, или характеристическая частота полинома.
Характерным для этой настройки является то, что отношение постоянных времени интегрирования
двух любых смежных разомкнутых контуров системы подчиненного регулирования равно 2:
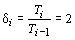 ,
,  ,
,
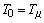 .
.
Если допустить вариацию отношений di, то ХП (1) примет вид:
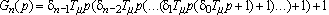
 ,
,
где
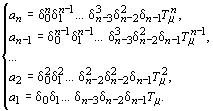
Нормируя полином (4) по его СГК
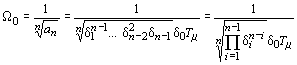
получаем:
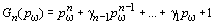
где
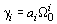
Из анализа коэффициентов (5) и выражения (8) вытекает эмпирическая формула [2]:
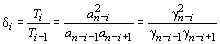 ,
,
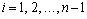 ,
,
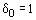 ,
,
где i – порядковый номер контура (счет начинается изнутри).
С ее помощью метод стандартных полиномиальных уравнений, используемый обычно при синтезе
СМУ, можно распространить и на СПР.
На важную роль коэффициентов di при синтезе систем автоматического управления обращено
внимание еще в работе [3], где они названы характеристическими соотношениями.
Недостатком применения полиномиального метода синтеза для систем подчиненного регулирования
является то, что при обеспечении желаемых динамических свойств системы при работе ее в линейном
режиме, может нарушиться динамика какого-либо из внутренних контуров при работе его в режиме
ограничения регулируемой им координаты. Чаще всего таким контуром является контур тока.
Для примера рассмотрим возможность использования в однократно интегрирующей системе подчиненного
регулирования скорости в качестве характеристического полинома (ХП) полинома Грехема-Летропа [4],
обеспечивающего минимизацию функционала
 ,
,
где e(t) – ошибка регулирования.
Для этого полинома отсутствуют аналитические методы определения коэффициентов и корней.
Его коэф-фициенты найдены эмпирически при использовании метода математического моделирования.
Полином Грехема-Летропа 3-го порядка имеет вид:
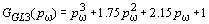 ,
,
Характеристические соотношения полинома (9) имеют следующие значения:
 ,
,
 .
.
Полином Баттерворта того же порядка, который является характеристическим полиномом
рассматривае-мой СПР при оптимизации ее методом двойных пропорций (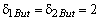 ),
выглядит следующим образом:
),
выглядит следующим образом:
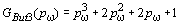 .
.
Используя для преобразования полиномов (11) и (12) к ненормированному виду формулы (6) и (8),
получаем:
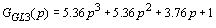 ,
,
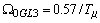 ;
;
 ,
,
 .
.
Применительно к рассматриваемой СПР
 ,
,
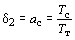 ,
,
где Тт , Тс – постоянные времени интегрирования разомкнутых контуров регулирования тока (КРТ)
и скорости (КРС) соответственно.
Переходные функции этих замкнутых контуров при сравниваемых настройках приведены на рис. 1.
Анализ рисунков показывает, что при использовании характеристического полинома Грехема-Летропа
переходная функция КРС, определяющая качество переходных процессов в системе электропривода при
работе всех ее элементов в линейном режиме, имеет меньшее перерегулирование
(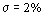 ) и более высокое быстродействие (время достижения максимума
) и более высокое быстродействие (время достижения максимума
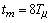 ), чем при использовании полинома Баттерворта (
), чем при использовании полинома Баттерворта ( ,
,
 ). Можно показать, что и статическое падение скорости в первом случае
будет меньше, чем во втором:
). Можно показать, что и статическое падение скорости в первом случае
будет меньше, чем во втором:
 .
.
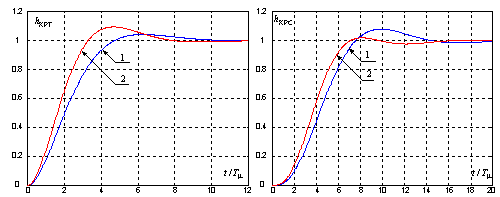
Рисунок 1 – Переходные функции КРТ (а) и КРС (б)
при использовании в КРС характеристического полинома
Баттерворта (1) и Грехема-Летропа (2)
Однако положительный эффект при использовании полинома Грехема-Летропа достигается за счет
более жесткой настройки контура тока, что приводит к увеличению перерегулирования его переходной
функции, которая определяет качество переходных процессов при работе привода в режиме
токоограничения.
Для того чтобы не изменять работу системы в режиме токоограничения, следует в регуляторе тока
оставить общепринятую настройку
 ,
,
а требуемое значение первого характеристического соотношения выбранного стандартного полинома
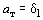 обеспечить за счет дополнительной отрицательной обратной связи по току,
заведенной на вход регулятора скорости с коэффициентом
обеспечить за счет дополнительной отрицательной обратной связи по току,
заведенной на вход регулятора скорости с коэффициентом
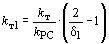 ,
,
где
kт – коэффициент передачи основной обратной связи по току;
kРС – коэффициент усиления регулятора скорости.
При этом коэффициент усиления регулятора скорости, синтезированного по общепринятой методике,
необходимо умножить на отношение
 .
.
Полученная таким образом СПР с дополнительной обратной связью по току, заведенной на вход
регулятора скорости, имеет переходную функцию контура тока, соответствующую оптимизации его
методом двойных пропорций, и переходную функцию контура скорости, соответствующую
характеристическому полиному Грехема-Летропа (кривая 2 на рис. 2). Следует отметить, что
при d1 > 2 дополнительная обратная связь по току становится положительной. Такое соотношение
характерно, в частности, для полинома Бесселя и полинома с биномиальными коэффициентами.
Для того чтобы иметь возможность при синтезе СПР выбирать произвольным образом не только
расположение нормированных полюсов, но и среднегеометрический корень, в [5] предложен метод
обобщенного полинома, применение которого часто приводит к синтезу нереализуемых регуляторов,
у которых порядок числителя пе-редаточной функции оказывается больше порядка знаменателя.
Избежать этого недостатка можно изменением постоянной времени тиристорного преобразователя (ТП)
путем охвата его обратной связью по ЭДС, что, собственно говоря, делают и в системах модального
управления. Величина измененной постоянной времени 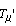 ТП зависит от
желаемого СГК
ТП зависит от
желаемого СГК  ж и характеристических соотношений
желаемого ХП:
ж и характеристических соотношений
желаемого ХП:
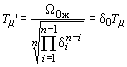 ,
,
 .
.
Коэффициент обратной связи по ЭДС преобразователя следует вычислять по формуле:
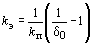 ,
,
где kп – коэффициент усиления ТП.
При замыкании преобразователя обратной связью изменяется не только его постоянная времени,
но и коэффициент усиления:
 ,
,
что необходимо учесть при синтезе регулятора тока.
Структурная схема системы подчиненного регулирования скорости, с особенностями, позволяющими
выполнить ее синтез методом стандартных полиномов, представлена на рис. 2.
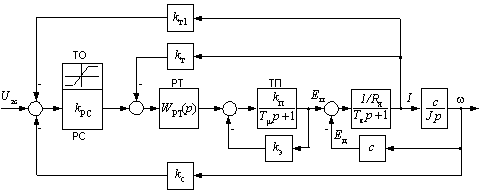
Рисунок 2 – Структурная схема СПР с
дополнительными
обратными связями по току и ЭДС преобразователя
Передаточные функции регуляторов тока и скорости на этой структурной схеме, в соответствии
с приведенными выше рассуждениями, должны иметь вид:
 ,
,
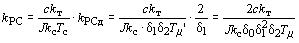 .
.
Из (18) следует, что при d0 > 1 обратная связь по ЭДС становится положительной, а постоянная
времени преобразователя не уменьшается, а увеличивается. В этом случае в контур регулирования
ЭДС лучше включить пропорционально-интегральный интегратор с передаточной функцией
 .
.
При этом изменится и передаточная функция регулятора тока:
 .
.
В заключение следует сказать, что непосредственное измерение ЭДС преобразователя проблематично,
а замена этого сигнала напряжением усложняет структуру объекта регулирования. Эта проблема
актуальна не только для СПР, но и для СМУ.
Идея ввода в систему подчиненного регулирования дополнительной обратной связи по току,
заведенной на вход регулятора скорости, может быть использована не только при синтезе СПР
полиномиальным методом, а во всех случаях, когда желаемая динамика контура скорости
обеспечивается при неудовлетворительной динамике контура тока.

 ,
, - относительный оператор Лапласа;
- относительный оператор Лапласа;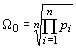 - СГК, или характеристическая частота полинома.
- СГК, или характеристическая частота полинома.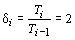 ,
,  ,
,
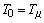 .
.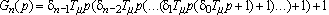
 ,
,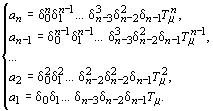
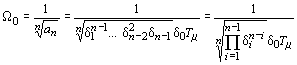
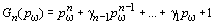
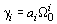
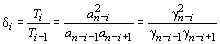 ,
,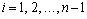 ,
,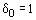 ,
, ,
,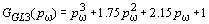 ,
, ,
, .
.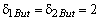 ),
выглядит следующим образом:
),
выглядит следующим образом: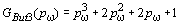 .
.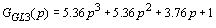 ,
,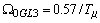 ;
; ,
, .
. ,
,
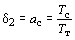 ,
,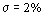 ) и более высокое быстродействие (время достижения максимума
) и более высокое быстродействие (время достижения максимума
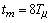 ), чем при использовании полинома Баттерворта (
), чем при использовании полинома Баттерворта ( ,
,
 ). Можно показать, что и статическое падение скорости в первом случае
будет меньше, чем во втором:
). Можно показать, что и статическое падение скорости в первом случае
будет меньше, чем во втором: .
.
 ,
,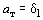 обеспечить за счет дополнительной отрицательной обратной связи по току,
заведенной на вход регулятора скорости с коэффициентом
обеспечить за счет дополнительной отрицательной обратной связи по току,
заведенной на вход регулятора скорости с коэффициентом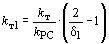 ,
, .
.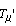 ТП зависит от
желаемого СГК
ТП зависит от
желаемого СГК  ж и характеристических соотношений
желаемого ХП:
ж и характеристических соотношений
желаемого ХП: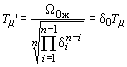 ,
, .
.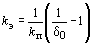 ,
, ,
,
 ,
,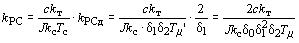 .
. .
. .
.