КОНСТРУИРОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ПО ЗАДАННОМУ
ПЕРЕРЕГУЛИРОВАНИЮ С УЧЕТОМ ХАРАКТЕРА ЗАТУХАНИЯ
ПЕРЕХОДНЫХ ПРОЦЕССОВ
О.И.Толочко
Донецкий Национальный Технический Университет
Украина,Донецк
Вісник Національного технічного університету “Харківський політехнічний ін-ститут”.
Збірка наукових праць. Тематичний випуск. – Харків: НТУ ХПІ. – 2003. – Т.2. – №10. – С.
315-319.
Одним из важнейших показателей качества переходных процессов является перерегулирование.
В связи с этим в [1] предложена методика конструирования передаточных функций линейных систем
автоматического управления (САУ), состоящая в том, что полюсы и нули системы располагаются
равномерно на окружности одинакового радиуса, а угол 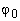 между
радиусами-векторами ближайших к мнимой оси (доминирующих) пар нулей и полюсов выбирается из
условия обеспечения заданного перерегулирования
между
радиусами-векторами ближайших к мнимой оси (доминирующих) пар нулей и полюсов выбирается из
условия обеспечения заданного перерегулирования 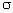 .
.
Ясно, что такой принцип синтеза можно применить для любого канонического расположения нулей и
полюсов. Проще всего размещать нули характеристического полинома (полюсы системы) и нули полинома
воздействия (нули системы) на окружности одного радиуса, равного значению средне-геометрического
корня 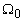 характеристического полинома (ХП). Но даже при таком ограничении, начиная с 4-го порядка,
можно получить бесконечное множество стандартных передаточных функций (ПФ) с одинаковым
перерегулированием, но разным показателем колебательности
характеристического полинома (ХП). Но даже при таком ограничении, начиная с 4-го порядка,
можно получить бесконечное множество стандартных передаточных функций (ПФ) с одинаковым
перерегулированием, но разным показателем колебательности 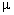 .
.
Задачей данной статьи является установить, как изменяется характер затухания переходных функций
с одинаковым перерегулированием при изменении взаимного расположения полюсов и нулей САУ на левой
полуокружности комплексной плоскости и дать рекомендации по конструированию передаточных функций
с учетом этого явления.
Для решения поставленной задачи рассмотрим, кроме предложенного в [1] еще 2 способа размещения
нулей и полюсов на окружности одного радиуса: 1) все комплексные корни образуют
комплексно-сопряженные пары; 2) проекции корней на мнимую ось делят ее на равные отрезки
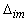 .
.
Все сравниваемые способы расположения полюсов на примере САУ с характеристическим полиномом 5-го
порядка изображены на рис. 1.

Рис.1. Некоторые способы взаимного расположения полюсов на окружности одного радиуса:
а) все комплексно-сопряженные пары расположены в одной точке;
б) все полюсы расположены на одинаковом угловом расстоянии друг от друга;
в) проекции полюсов на мнимую ось делят ее на равные отрезки
Для случая, соответствующего рис. 1а, при четном порядке ХП (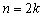 ) все полюсы системы образуют
кратные комплексно-сопряженные пары
) все полюсы системы образуют
кратные комплексно-сопряженные пары

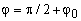 ,
,
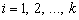 ,
,
а при нечетном n (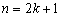 ), кроме кратных комплексно-сопряженных корней (1),
существует еще один действительный корень
), кроме кратных комплексно-сопряженных корней (1),
существует еще один действительный корень  .
.
При этом характеристический полином можно сконструировать по следующей формуле:

где
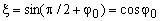
– коэффициент демпфирования комплексно-сопряженных полюсов.
Для случая, соответствующего рис. 1а, доминирующая пара комплексно-сопряженных полюсов
системы определяется выражениями
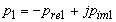 ,
,

а проекции всех остальных полюсов на мнимую ось делят ее отрезок [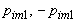 ] на равные части:
] на равные части:
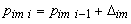 ,
,

где
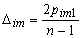 ,
,
 .
.
С учетом того, что все полюсы расположены на окружности радиуса  ,
действительные части полюсов можно рассчитать по формуле
,
действительные части полюсов можно рассчитать по формуле
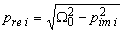 .
.
По известным полюсам конструируется характеристический полином:
 ,
,
 .
.
Задачей синтеза в обоих случаях является определение угла 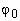 из условия обеспечения заданного
перерегулирования переходной функции. Зная этот угол, по приведенным выше формулам можно легко
определить как нули, так и коэффициенты ХП.
из условия обеспечения заданного
перерегулирования переходной функции. Зная этот угол, по приведенным выше формулам можно легко
определить как нули, так и коэффициенты ХП.
Прежде, чем решать эту задачу, рассмотрим графики переходных процессов рис. 2, 3 САУ с
передаточной функцией (ПФ)

для трех сравниваемых здесь вариантов расположения полюсов, обеспечивающих 15%- и 2%-ое значения
перерегулирования соответственно. Отметим также, что размещение полюсов на рис. 1 соответствует
15%-ому перерегулированию переходных процессов.
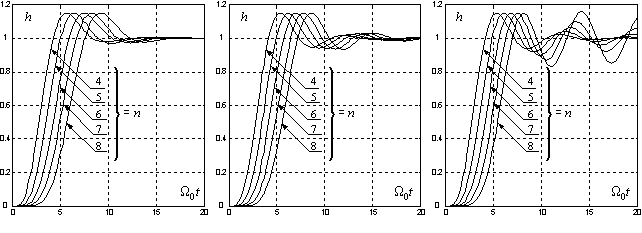
Рис. 2. Переходные функции САУ с нулевым порядком полинома воздействия при
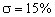
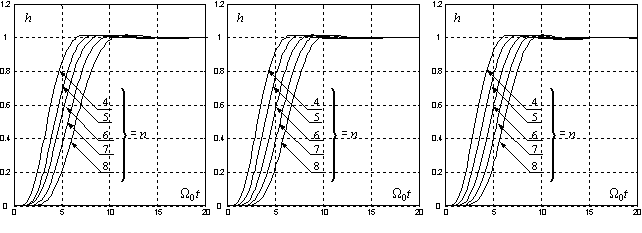
Рис. 3. Переходные функции САУ с нулевым порядком полинома воздействия при

Из анализа рис. 1 следует, что при одном и том же перерегулировании распределение «а»
отличается наименьшим, а распределение «в» – наибольшим показателями колебательности m. Это
определяет и поведение переходных функций на стадии их затухания.
Поскольку с уменьшением перерегулирования уменьшается и угол m, то и характер затухания
переходных процессов при этом становится менее колебательным. При синтезе систем управления
электромеханическими объектами стремятся обеспечить такую форму переходной функции, чтобы после
достижения своего максимального значения она затухала как можно быстрее, но с небольшим и
единственным «обратным перерегулированием». Исходя из этих требований каждое из рассматриваемых
распределений можно применять только для определенного диапазона перерегулирований. Из анализа
графиков переходных процессов можно рекомендовать распределение «а» для 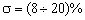 ,
распределение «б» для
,
распределение «б» для 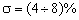 , а распределение «в» для
, а распределение «в» для 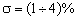 .
.
На рис. 4 приведены графики зависимостей 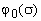 для ХП c кратными комплексно-сопряженными корнями
(а) и ХП, проекции нулей которых на мнимую ось комплексной плоскости делят ее на равные отрезки
(б).
для ХП c кратными комплексно-сопряженными корнями
(а) и ХП, проекции нулей которых на мнимую ось комплексной плоскости делят ее на равные отрезки
(б).
Рис. 4. Графики зависимостей 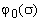 для ХП (4-7)-го порядков
для ХП (4-7)-го порядков
Для повышения быстродействия дополним ПФ (10) полиномом воздействия, нули которого размещаются
на окружности радиуса 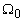 по тем же правилам, что и нули характеристического полинома:
по тем же правилам, что и нули характеристического полинома:
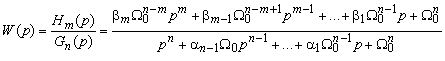 .
.
При таком подходе коэффициенты полинома воздействия можно определять по той же методике, что
и коэффициенты соответствующего ХП. Особенностью предлагаемой методики синтеза является то,
что сначала синтезируют знаменатель передаточной функции, а затем ее числитель. При этом
предполагается, что нули и полюсы не взаимосвязаны друг с другом, т.е. изменение нулей САУ не
приводит к изменению ее полюсов и наоборот.
Исследования показали, что величина угла  между радиусами-векторами доминирующей пары нулей
и мнимой осью, а, следовательно, и коэффициенты полинома воздействия практически не зависят от
порядка характеристического полинома, а определяются только величиной заданного
перерегулирования.
между радиусами-векторами доминирующей пары нулей
и мнимой осью, а, следовательно, и коэффициенты полинома воздействия практически не зависят от
порядка характеристического полинома, а определяются только величиной заданного
перерегулирования.
Например, для обеспечения для обеспечения 10%-го перерегулирования при кратных
комплексно-сопряженных нулях и полюсах ХП 6-го и 7-го порядков, нормированные по
средне-геометрическому корню характеристического полинома (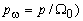 имеют вид
имеют вид
 ,
,
а полиномы воздействия могут быть выбраны по формулам
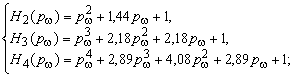
для обеспечения 1%-го перерегулирования при разбиении на равные отрезки мнимой оси проекциями
полюсов и нулей нормированные характеристические полиномы и полиномы воздействия имеют следующий
вид:
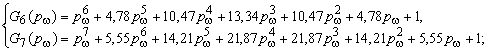
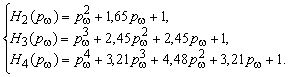
Переходные функции систем с такими передаточными функциями показаны на рис. 5, 6.
Абсолютные отклонения перерегулирований от заданных значений при предложенном упрощенном
синтезе полиномов воздействия не превышает 0,3%, что вполне допустимо для инженерных расчетов.
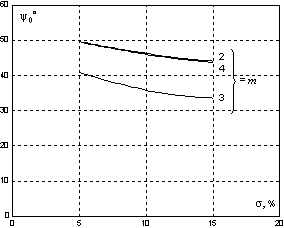
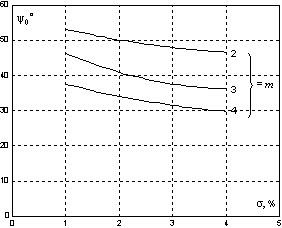
На рис. 7 приведены графики зависимостей 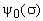 для полиномов воздействия c кратными
комплексно-сопряженными нулями (а) и полиномов воздействия, проекции нулей которых на мнимую
ось комплексной плоскости делят ее на равные отрезки (б). Следует подчеркнуть, что графики
рис. 5-7 получены при конструировании передаточных функций САУ как при нулевом, так и при
отличном от нуля порядках полинома воздействия из условий достижения одинаковых перерегулирований
переходных функций.
для полиномов воздействия c кратными
комплексно-сопряженными нулями (а) и полиномов воздействия, проекции нулей которых на мнимую
ось комплексной плоскости делят ее на равные отрезки (б). Следует подчеркнуть, что графики
рис. 5-7 получены при конструировании передаточных функций САУ как при нулевом, так и при
отличном от нуля порядках полинома воздействия из условий достижения одинаковых перерегулирований
переходных функций.
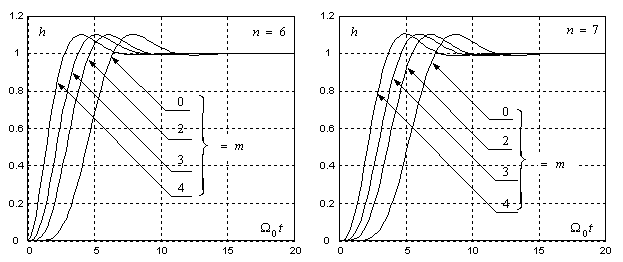
Рис. 5. Переходные функции САУ с ПФ (9) с кратными комплексно-сопряженными нулями
и полюсами при 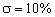
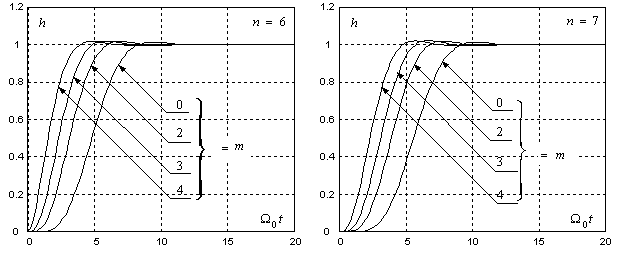
Рис. 6. Переходные функции САУ с ПФ (9) с нулями и полюсами, проекции которых на
мнимую ось делят ее на равные отрезки, при 
Рис. 7. Графики зависимостей  для полиномов воздействия (2-4)-го порядков
для полиномов воздействия (2-4)-го порядков
Выводы
- При размещении полюсов системы в левой половине комплексной плоскости на окружности одного
радиуса при разных законах их взаимного расположения одно и то же значение перерегулирование
переходной функции может быть обеспечено при разном характере ее затухания.
- Наименьший показатель колебательности при заданном перерегулировании имеют системы с
кратными комплексно-сопряженными полюсами, что дает возможность использовать такое распределение
для сравнительно больших значений перерегулирования (до 20%). При малых перерегулированиях
процесс уменьшения переходной функции протекает апериодически и слишком медленно.
- Более быстрое затухание переходной функции от максимума до установившегося значения при
малых значениях заданного перерегулирования (1ё4 %) обеспечивает распределение, при котором
проекции полюсов на мнимую ось делят ее на равные отрезки. При больших перерегулированиях
процесс затухания переходной функции при таком размещении полюсов становится излишне
колебательным и длительным.
- Промежуточными свойствами в отношении характера и скорости затухания переходных процессов
среди рассмотренных ХП занимает характеристический полином с равномерным размещением полюсов
на окружности одного радиуса. Его целесообразно применять для обеспечения (5ё8)%-ного заданного
перерегулирования переходной функции.
- Для увеличения быстродействия системы с сохранением заданного перерегулирования ее
передаточную функцию можно снабдить полиномом воздействия, синтезированным по тем же правилам,
что и характеристический полином. Коэффициенты такого полинома воздействия практически не
зависят от порядка характеристического полинома.
Литература
- 1. Коцегуб П.Х., Толочко О.И., Розкаряка П.И. Конструирование передаточных функций
линейных САУ по заданному перерегулированию // Вісник Національного технічного університету
ХПІ. Серія “Електромеханіка, електроніка і електропривод”. №10. - Харків, НТУ ХПІ, 2001. -
С.95-98.
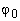 между
радиусами-векторами ближайших к мнимой оси (доминирующих) пар нулей и полюсов выбирается из
условия обеспечения заданного перерегулирования
между
радиусами-векторами ближайших к мнимой оси (доминирующих) пар нулей и полюсов выбирается из
условия обеспечения заданного перерегулирования 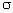 .
.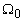 характеристического полинома (ХП). Но даже при таком ограничении, начиная с 4-го порядка,
можно получить бесконечное множество стандартных передаточных функций (ПФ) с одинаковым
перерегулированием, но разным показателем колебательности
характеристического полинома (ХП). Но даже при таком ограничении, начиная с 4-го порядка,
можно получить бесконечное множество стандартных передаточных функций (ПФ) с одинаковым
перерегулированием, но разным показателем колебательности 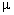 .
.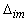 .
.
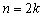 ) все полюсы системы образуют
кратные комплексно-сопряженные пары
) все полюсы системы образуют
кратные комплексно-сопряженные пары
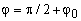 ,
,
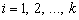 ,
,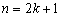 ), кроме кратных комплексно-сопряженных корней (1),
существует еще один действительный корень
), кроме кратных комплексно-сопряженных корней (1),
существует еще один действительный корень  .
.
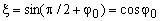
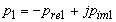 ,
,

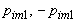 ] на равные части:
] на равные части: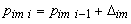 ,
,

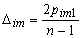 ,
,
 .
. ,
действительные части полюсов можно рассчитать по формуле
,
действительные части полюсов можно рассчитать по формуле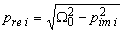 .
. ,
,
 .
.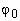 из условия обеспечения заданного
перерегулирования переходной функции. Зная этот угол, по приведенным выше формулам можно легко
определить как нули, так и коэффициенты ХП.
из условия обеспечения заданного
перерегулирования переходной функции. Зная этот угол, по приведенным выше формулам можно легко
определить как нули, так и коэффициенты ХП.

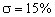


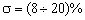 ,
распределение «б» для
,
распределение «б» для 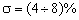 , а распределение «в» для
, а распределение «в» для 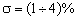 .
.
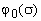 для ХП c кратными комплексно-сопряженными корнями
(а) и ХП, проекции нулей которых на мнимую ось комплексной плоскости делят ее на равные отрезки
(б).
для ХП c кратными комплексно-сопряженными корнями
(а) и ХП, проекции нулей которых на мнимую ось комплексной плоскости делят ее на равные отрезки
(б).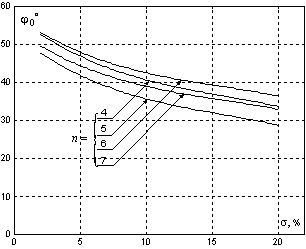

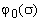 для ХП (4-7)-го порядков
для ХП (4-7)-го порядков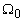 по тем же правилам, что и нули характеристического полинома:
по тем же правилам, что и нули характеристического полинома: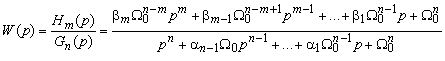 .
. между радиусами-векторами доминирующей пары нулей
и мнимой осью, а, следовательно, и коэффициенты полинома воздействия практически не зависят от
порядка характеристического полинома, а определяются только величиной заданного
перерегулирования.
между радиусами-векторами доминирующей пары нулей
и мнимой осью, а, следовательно, и коэффициенты полинома воздействия практически не зависят от
порядка характеристического полинома, а определяются только величиной заданного
перерегулирования.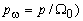 имеют вид
имеют вид ,
,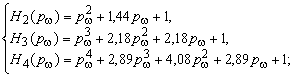
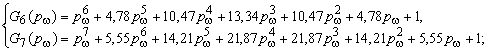
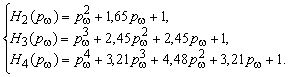
 для полиномов воздействия c кратными
комплексно-сопряженными нулями (а) и полиномов воздействия, проекции нулей которых на мнимую
ось комплексной плоскости делят ее на равные отрезки (б). Следует подчеркнуть, что графики
рис. 5-7 получены при конструировании передаточных функций САУ как при нулевом, так и при
отличном от нуля порядках полинома воздействия из условий достижения одинаковых перерегулирований
переходных функций.
для полиномов воздействия c кратными
комплексно-сопряженными нулями (а) и полиномов воздействия, проекции нулей которых на мнимую
ось комплексной плоскости делят ее на равные отрезки (б). Следует подчеркнуть, что графики
рис. 5-7 получены при конструировании передаточных функций САУ как при нулевом, так и при
отличном от нуля порядках полинома воздействия из условий достижения одинаковых перерегулирований
переходных функций.
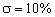


 для полиномов воздействия (2-4)-го порядков
для полиномов воздействия (2-4)-го порядков