
При повышении частоты приложенного напряжения раньше или позже начинает проявляться размагничивающий эффект вихревых токов в стали, что выражается в вытеснении магнитного потока из середины листов к их периферии. Для анализа этого вопроса обратимся к рис. 1-13, где изображен лист стали и нанесены оси координат.Начало координат выбрано и середине листа стали. Индукция В и напряженность магнитного поля Н направлены по осп у. Пренебрегая искривлением линий тока у краев листа в связи с тем, что толщина листа стали мала по сравнению с его шириной и длиной, можно считать вектор плотности тока направленным параллельно поверхности листа и перпендикулярно направлению магнитной индукции. При t меньше l и t меньше h электромагнитную волну можно считать плоской. Полагаем также магнитную проницаемость стали постоянной.

Уравнение Максвелла для плоской волны в проводящей среде имеет вид:
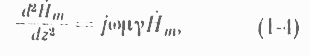
где Нт - комплексная амплитуда напряженности магнитного ноля; w = 2nf - угловая частота переменного тока; m и у - магнитная проницаемость и электрическая проводимость. Решение этого уравнения имеет вид:
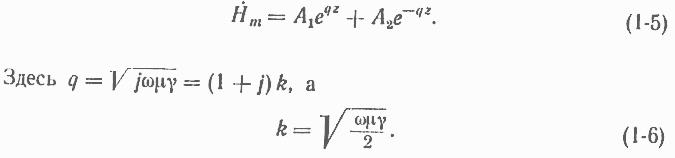
Постоянные интегрирования А1 и A2 могут быть найдены из граничных условий. При z = ±t/2, Нт - Нте, где Нте - напряженность поля па поверхности листа. Отсюда

Подставляя эти значения в (1-5), получим
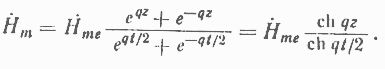
Комплексные амплитуды магнитной индукции и плотности тока будут
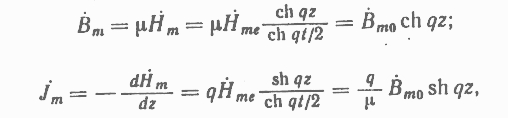
Bto индукция в середине листа стали (при z = 0).
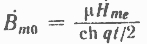
Найдем среднее значение индукции по толщине листа:

Выражения для модулей Вm и Jm имеют вид:
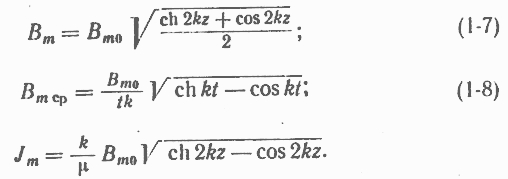
Используя выражение (1-8), получим
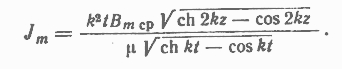
Потери в элементарном объеме листа толщиной dz будут:
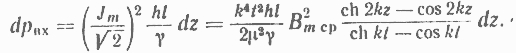
Потери во всем объеме листа получим, проинтегрировав это выражение по толщине листа, а удельные потери в единице веса получим, разделив их на вес листа, т. е. на hltб, где б - удельный вес трансформаторной стали. Таким образом, удельные потери
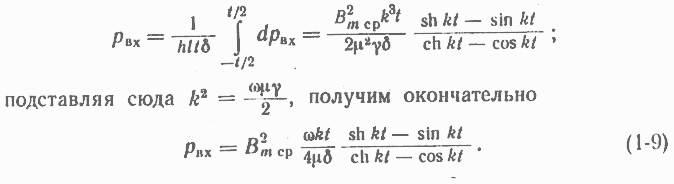
Разделив (1-9) на (1-3) и обозначив потери от вихревых токов без учета их размагничивающего действия через Pвх ," найдем относительное уменьшение потерь в стали от вихревых токов, вызванное размагничивающим действием этих токов:
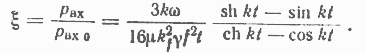
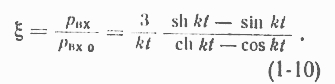
Таким образом, уменьшение потерь от вихревых токов вследствие их размагничивающего действия является функцией параметра kt.
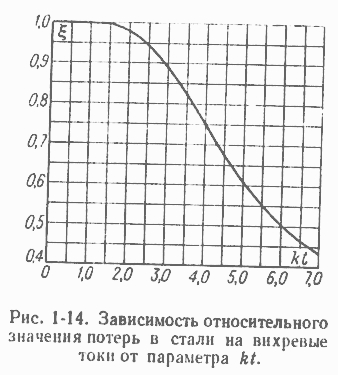
На рис. 1-14 соответственно формуле (1-10) построена зависимость f(kt), размагничивающим действием вихревых токов можно пренебречь.
Формула (1-10) упрощается:
