§ 7.2. Использование метода узловых напряжений при расчете переходных процессов.

Анализ резистивных цепей, исторически первый из разделов тео­рии электрических цепей, в настоящее время считается и наиболее разработанным. Поэтому задачи других разделов [расчет переход­ных процессов (см. § 7.1), диагностика электрических цепей (см. § 8.9), анализ коммутаций в цепях из реактивных элементов (см. § 9.4)] часто стараются свести к анализу резистивных цепей, рассматривая методы их решения как расчетный эталон. Для выбора из многообразия подобных методов (узловых напряжений, контур­ных токов, смешанных величин, топологических преобразований и т. д.), наиболее адекватного расчету переходных процессов с по­мощью синтетических схем, отметим основную особенность анализа переходных процессов, заключающуюся в необходимости расчета многих (до тысяч и даже десятков тысяч) точек дискретизации. По­этому предпочтение должно быть отдано такому методу анализа резистивных цепей, процедура формирования уравнений в котором наиболее экономична по вычислительным затратам, а сами уравне­ния характеризуются свойствами, гарантирующими получение ус­тойчивого решения на каждом шаге дискретизации, с тем чтобы обеспечивалась заданная точность расчета переходного процесса на длительных интервалах времени. Кроме того, необходимо, что­бы выбранный метод был универсальным в смысле возможности его использования при расчете цепей с невзаимными, нелинейными и многополюсными элементами. Исходя из этих требований предпоч­тение отдается методу узловых напряжений. Этот метод универ­сален, отличается наиболее простой для машинной реализации процедурой формирования уравнений, свойства которых обеспечивают высокую скорость сходимости наиболее распростра­ненных методов численного решения алгебраических систем. Рас­смотрим этот метод подробнее.

Суть метода заключается в сле­дующем. Пусть имеется GJ-цепь (цепь, элементы которой суть про­водимости и источники тока), содержащая n+1 узел. Параметры источников тока и проводимостей ветвей цепи считаются извест­ными. Требуется определить напряжения и неизвестные токи вет­вей цепи. Пронумеруем все узлы цепи цифрами 0, 1, 2, ... и обозна­чим через Uk, k=1, 2, … напряжение (узловое напряжение) меж­ду узлом k и опорным узлом 0. Для нахождения этих напряжений по методу узловых напряжений составляют систему уравнений

где U — матрица-столбец (вектор) узловых напря­жений; J — матрица-столбец (вектор) известных за­дающих токов; Y - матрица известных узловых про­водимостей. При этом элемент Jk, k=1, 2, ..., n, вектора J представ­ляет собой алгебраическую сумму токов источников тока ветвей, присоединенных к узлу k. Эти значения берут с положительным знаком, если ток источника направлен к узлу k, и с отрицательным, если ток источника направлен от узла k. Диагональный элемент матрицы Y, называемый собственной прово­димостью k-го узла, представляет собой сумму проводимостей всех ветвей, присоединенных к узлу k. Недиагональный элемент  матрицы Y, называемый общей проводимостыо узлов i  и j, равен сумме проводимостей ветвей, соединяющих
узлы I и j, взятой с обратным знаком.     
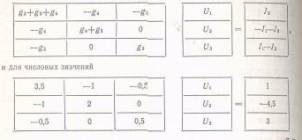
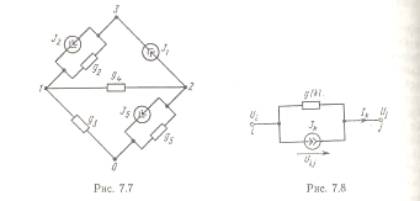
Пример  7.2. Для цепи, изображенной на рис.  7.7, уравнение (7.5) имеет вид:

 

 

Отметим, что каждое k-е, k= 1, 2,..., п, уравнение в системе (7.5)   представляет собой запись для k-го узла первого закона Кирхгофа, выраженного через узловые напряжения.

 

Решение системы (7.5) позволяет получить искомые значения узловых напряжений. Последующий расчет цепи не представляет сложности.

Отметим, что все элементы матрицы У^-1, называе­мой матрицей узловых сопротивлений, положительны. Такую мат­рицу также называют положительной, т. е. R>0. Для обоснования этого свойства рассмотрим произвольный элемент  матрицы R. Численно он равен напряжению i-го узла цепи, вызванному единич­ным задающим током узла j, в предположении, что задающие токи других узлов равны нулю. Подобное напряжение для резистивной взаимной цепи всегда положительно. Матрицы с неположительны­ми внедиагональными элементами, которым соответствуют положи­тельные обратные матрицы, называют М-матрицами. Симметрич­ные М-матрицы называют матрицами Стилтьеса. Таким образом, Y-матрицы линейных взаимных цепей являются матрицами Стилтье­са, а Y-матрицы невзаимных цепей являются, как правило, М-мат­рицами. Заметим, что спектр М-матриц — вещественный положи­тельный. Это обстоятельство существенно при решении систем урав­нений узловых напряжений (узловых уравнений), поскольку гаран­тирует сходимость наиболее распространенных итерационных ме­тодов и позволяет оценить ее скорость.