ОЦЕНКА ПОГРЕШНОСТИ ИЗМЕРЕНИЙ НЕСИНУСОИДАЛЬНОСТИ НАПРЯЖЕНИЯ
В ДЕЙСТВУЮЩИХ ЭЛЕКТРИЧЕСКИХ СЕТЯХ
Коломытцев А.Д., Майоров А.Л.
Донецкий национальный технический университет
The estimation of voltage nonsinusoidality by periodic and random
character of voltage sinusoid derivation is considered in this paper.
That is made by devices the work principle of which is based on appearance of
interference as Fourier series. Deviation of measurement is estimated by interference
dispersion.
Исследования несинусоидальности напряжения,
проводимые в действующих электрических сетях, показывают, что искажения синусоиды
напряжения носят, как правило, случайный характер [1,2]. Поэтому оценка качества
напряжения по величинам коэффициентов несинусоидальности, нормируемым в [4], является
неопределенной, поскольку эти показатели предполагают периодический характер искажений.
Очевидно, что применение приборов, измеряющих эти коэффициенты и использующих принцип
разложения в ряд Фурье, приведет к погрешности в оценке качества напряжения [3].
Таким образом актуальными становятся вопросы возможности использования таких приборов
для экспериментальных исследований, а также эквивалентирования случайных искажений для их
сравнения с требованиями [4].
Получаемые с помощью измерителей несинусоидальности (ИН)
статистические характеристики зависят не только от вида процесса
u(t) изменения мгновенных
значений напряжения, но и от параметров ИН. При планировании экспериментальных исследований
и использовании результатов измерений необходимо оценивать погрешность, вносимую ИН [3].
Отличие формы кривой напряжения от синусоидальной будем
называть помехой. В общем случае помеха - это процесс
uп(t) на выход идеального фильтра,
пропускающего без искажений сигналы на частотах
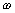 , больших основной
, больших основной 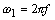 ,
где f=50Гц.
,
где f=50Гц.
 Можно считать, что ИН не пропускает сигналы с частотой меньшей основной,
а его узкополосные фильтры настроены на частоты
Можно считать, что ИН не пропускает сигналы с частотой меньшей основной,
а его узкополосные фильтры настроены на частоты
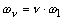 (
(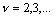 ),
кратные
),
кратные 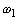 .
То есть, эти фильтры имеют амплитудно-частотные
характеристики (АЧХ) (рис. 1.), максимумы которых
.
То есть, эти фильтры имеют амплитудно-частотные
характеристики (АЧХ) (рис. 1.), максимумы которых
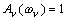 .
Для упрощения АЧХ фильтров могут быть заменены
прямоугольниками единичной высоты, основанием которого
является энергетическая полоса пропускания
.
Для упрощения АЧХ фильтров могут быть заменены
прямоугольниками единичной высоты, основанием которого
является энергетическая полоса пропускания 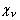 фильтра,
определяемая из условия эквивалентности площадей
фактической и прямоугольной АЧХ.
Предположим, что помеха имеет периодический характер.
В этом случае она может быть представлена дискретным спектром гармонических
составляющих
фильтра,
определяемая из условия эквивалентности площадей
фактической и прямоугольной АЧХ.
Предположим, что помеха имеет периодический характер.
В этом случае она может быть представлена дискретным спектром гармонических
составляющих 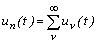 .
В стационарном состоянии достаточным условием
ИН является непересекаемость АЧХ смежных частот настройки, т.е. АЧХ любого
фильтра должна обращаться в нуль на участках
.
В стационарном состоянии достаточным условием
ИН является непересекаемость АЧХ смежных частот настройки, т.е. АЧХ любого
фильтра должна обращаться в нуль на участках 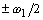 относительно
относительно 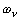 ,
так что
,
так что  .
ИН будет измерять действующие значения процессов
.
ИН будет измерять действующие значения процессов 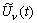 на выходе каждого фильтра за время tf =1/f. Проделав
измерения на всех частотах, можно определить величину коэффициента несинусоидальности
на выходе каждого фильтра за время tf =1/f. Проделав
измерения на всех частотах, можно определить величину коэффициента несинусоидальности
 .
(1)
Погрешность определения будет зависеть только от числа n учитываемых гармоник:
.
(1)
Погрешность определения будет зависеть только от числа n учитываемых гармоник:
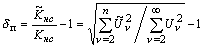 (2)
Любая гармоника с амплитудой
(2)
Любая гармоника с амплитудой 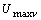 имеет нулевое среднее значение и дисперсию
имеет нулевое среднее значение и дисперсию  .
Поэтому выраженная в о.е. дисперсия помехи
.
Поэтому выраженная в о.е. дисперсия помехи
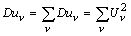 (3)
совпадает с нормируемым в [4] коэффициентом несинусоидальности. Физический смысл
(3)
совпадает с нормируемым в [4] коэффициентом несинусоидальности. Физический смысл
 заключается в том, что она пропорциональна энергии гармоник, выделяемой на активном сопротивлении. С учетом (3) относительная погрешность (2) может быть определена как
заключается в том, что она пропорциональна энергии гармоник, выделяемой на активном сопротивлении. С учетом (3) относительная погрешность (2) может быть определена как
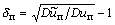 (4)
При периодических изменениях напряжения основной
частоты с циклом tц в ряд Фурье входят гармонические составляющие
(назовем их
(4)
При периодических изменениях напряжения основной
частоты с циклом tц в ряд Фурье входят гармонические составляющие
(назовем их 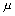 -гармоники)
частоты которых кратны
-гармоники)
частоты которых кратны 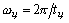 .
При больших циклах (tц>>tf ) спектр
.
При больших циклах (tц>>tf ) спектр
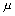 -гармоник
практически не попадает в полосу частот больших
-гармоник
практически не попадает в полосу частот больших 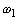 ,
поэтому ИН не воспринимает полезный сигнал как помеху. Измерения будут
производиться теоретически точно, поскольку
,
поэтому ИН не воспринимает полезный сигнал как помеху. Измерения будут
производиться теоретически точно, поскольку 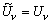 ,
а погрешности возникают из-за ограниченного количества N учитываемых гармоник и
отклонений
,
а погрешности возникают из-за ограниченного количества N учитываемых гармоник и
отклонений 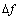 частоты.
Линии фактического спектра при уменьшении частоты будут сдвинуты влево относительно
частот настройки на величины
частоты.
Линии фактического спектра при уменьшении частоты будут сдвинуты влево относительно
частот настройки на величины 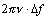 тем больше, чем больше номер гармоники. Поэтому, погрешность будет равна
тем больше, чем больше номер гармоники. Поэтому, погрешность будет равна
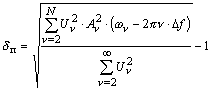 .
Если же tц будет соизмерим с tf , то требование
непересекаемости АЧХ уже не будет являться достаточным. Например, при идеальном
широтно-импульсном управлении тиристорами (рис. 2) за время включения tв и
tц укладываются целое число В периодов синусоиды.
.
Если же tц будет соизмерим с tf , то требование
непересекаемости АЧХ уже не будет являться достаточным. Например, при идеальном
широтно-импульсном управлении тиристорами (рис. 2) за время включения tв и
tц укладываются целое число В периодов синусоиды.
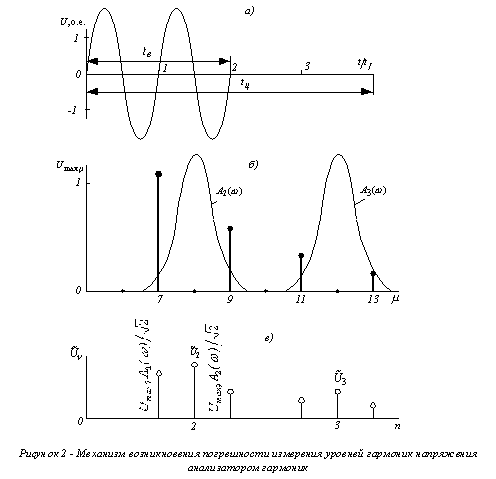 Как показано в [3] каждая из m захватываемых АЧХ
Как показано в [3] каждая из m захватываемых АЧХ 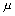 -гармоник преобразуется фильтром в гармоническую составляющую амплитудой
-гармоник преобразуется фильтром в гармоническую составляющую амплитудой
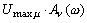 . На выходе ИН будут показания:
. На выходе ИН будут показания:
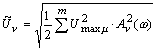 ,
хотя теоретически
,
хотя теоретически  .
Для обеспечения точности измерений необходимо, чтобы АЧХ каждого фильтра
обращалась в нуль на интервале
.
Для обеспечения точности измерений необходимо, чтобы АЧХ каждого фильтра
обращалась в нуль на интервале 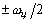 относительно
относительно 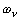 , так что
, так что
 .
Таким образом при строго периодических помехах
надлежащим выбором АЧХ фильтров ИН можно обеспечить достоверность оценок
несинусоидальности напряжения.
.
Таким образом при строго периодических помехах
надлежащим выбором АЧХ фильтров ИН можно обеспечить достоверность оценок
несинусоидальности напряжения.
 Перейдем к рассмотрению случайных помех.
В этом случае понятия гармоник не существует, что исключает возможность
применения формул (1-3). Если помеха представляет собой стационарный случайный
процесс с независящими от времени характеристиками, то применительно к
выражению (4) достаточно задать корреляционную функцию
Перейдем к рассмотрению случайных помех.
В этом случае понятия гармоник не существует, что исключает возможность
применения формул (1-3). Если помеха представляет собой стационарный случайный
процесс с независящими от времени характеристиками, то применительно к
выражению (4) достаточно задать корреляционную функцию
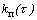 или спектральную
плотность
или спектральную
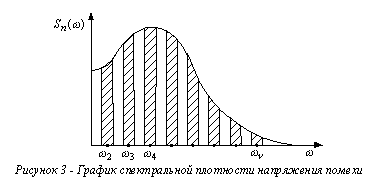
плотность 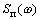 помехи. Дисперсия помехи
помехи. Дисперсия помехи
 геометрически равна площади под графиком
геометрически равна площади под графиком 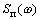 (рис. 3).
В установившемся режиме на выходе ИН будут показания
(рис. 3).
В установившемся режиме на выходе ИН будут показания
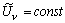 . В соответствии
с общими формулами теории случайных процессов для характеристик процесс
. В соответствии
с общими формулами теории случайных процессов для характеристик процесс
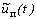 на выходе
ИН получим выражения
на выходе
ИН получим выражения
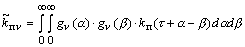 ,
,
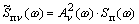 (4)
(4)
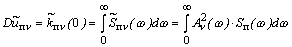 .
(5)
где
.
(5)
где 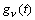 - импульсная
характеристика фильтра;
- импульсная
характеристика фильтра;  и
и
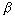 - переменные интегрирования.
Так как длительность колебаний помехи намного меньше
tf, то показания ИН
- переменные интегрирования.
Так как длительность колебаний помехи намного меньше
tf, то показания ИН 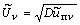 .
Геометрический смысл показаний ИН наглядно
прослеживается в случае идеального узкополосного фильтра, у которого в пределах
полосы пропускания
.
Геометрический смысл показаний ИН наглядно
прослеживается в случае идеального узкополосного фильтра, у которого в пределах
полосы пропускания  АЧХ равна единице. Учитывая (5), получим
АЧХ равна единице. Учитывая (5), получим
 .
Для такого фильтра величина
.
Для такого фильтра величина 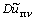 (5) равна площади
(5) равна площади 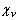
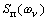 ,
вырезаемой из графика спектральной плотности прямоугольником АЧХ (рис. 3).
Если
,
вырезаемой из графика спектральной плотности прямоугольником АЧХ (рис. 3).
Если 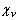 мала и в
пределах этой полосы пропускания спектральная плотность может быть
линеаризирована, то величина
мала и в
пределах этой полосы пропускания спектральная плотность может быть
линеаризирована, то величина 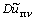 пропорциональна значению этой спектральной плотности
пропорциональна значению этой спектральной плотности
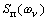 при частоте
настройки фильтра
при частоте
настройки фильтра 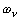 . Поэтому
. Поэтому
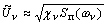 .
(6)
Несинусоидальность стационарной помехи оценивается по дисперсии
.
(6)
Несинусоидальность стационарной помехи оценивается по дисперсии
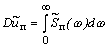 .
(7)
Соотношения (3) и (7) подчеркивают принципиальное
отличие непериодической помехи от периодической, обусловленное необходимостью
перехода от ряда к интегралу Фурье. Величины выражения (6) нельзя считать
"уровнями гармоник", так как понятие гармоники для случайных процессов не
существует. Если формально оценить несинусоидальность по (3)
.
(7)
Соотношения (3) и (7) подчеркивают принципиальное
отличие непериодической помехи от периодической, обусловленное необходимостью
перехода от ряда к интегралу Фурье. Величины выражения (6) нельзя считать
"уровнями гармоник", так как понятие гармоники для случайных процессов не
существует. Если формально оценить несинусоидальность по (3)
 ,
то будет допущена погрешность
,
то будет допущена погрешность
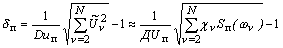 .
То есть, вместо всей площади под графиком, равной дисперсии помехи, суммируются
только площади заштрихованных трапеций. Поскольку полосы пропускания не
пересекаются, то погрешность будет отрицательной, а оценка несинусоидальности заниженной.
Таким образом, в случае стационарной случайной
помехи ИН следует применять в качестве анализатора спектральной плотности.
График
.
То есть, вместо всей площади под графиком, равной дисперсии помехи, суммируются
только площади заштрихованных трапеций. Поскольку полосы пропускания не
пересекаются, то погрешность будет отрицательной, а оценка несинусоидальности заниженной.
Таким образом, в случае стационарной случайной
помехи ИН следует применять в качестве анализатора спектральной плотности.
График 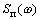 строится как огибающая значений
строится как огибающая значений
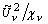 , получаемых для
разных частот. Из-за стационарности помехи измерения на разных частотах
необязательно проводить одновременно.
, получаемых для
разных частот. Из-за стационарности помехи измерения на разных частотах
необязательно проводить одновременно.
Еще большие трудности возникают в случае
нестационарной помехи. В этом случае понятие спектральной плотности не имеет
физического смысла и практически использовать можно только корреляционную функцию
kп(t1 , t2 ), которая
зависит от времени: при t1=t,
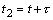 . Дисперсия помехи
будет определяться выражением
. Дисперсия помехи
будет определяться выражением
Duп=kп(t1 .
Дисперсия процесса на выходе фильтра ИН
 ,
(8)
а также показания ИН
,
(8)
а также показания ИН  зависит от времени.
зависит от времени.
Как и в случае стационарной помехи, формальное
использование формулы (3) дает погрешность
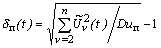 ,
уменьшить которую не представляется возможным, так как даже для идеального
полосового фильтра в отличие от описываемого выражением (6) трудно связать
дисперсию (8) с корреляционной функцией помехи.
,
уменьшить которую не представляется возможным, так как даже для идеального
полосового фильтра в отличие от описываемого выражением (6) трудно связать
дисперсию (8) с корреляционной функцией помехи.
При нестационарной помехе измерения на выходах
всех фильтров нужно производить одновременно, а обработку результатов вести по n
ансамблям реализаций процессов 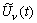 .
.
Таким образом можно сделать вывод о том, что при
оценке несинусоидальности напряжения с помощью ИН, использующих принцип
разложения в ряд Фурье, необходимо:
- определить вид помехи;
- при периодической помехе достаточно однократного измерения, а надлежащим
выбором АЧХ фильтров можно обеспечить достоверность оценок несинусоидальности
напряжения. Для обычно встречающегося на практике случая стационарной
непериодической помехи по показаниям ИН следует построить статистическую
спектральную плотность, применяя для оценки несинусоидальности формулу (7).
- при нестационарной помехе применение ИН не обеспечивает достоверность оценки
несинусоидальности.
ЛИТЕРАТУРА
1. Куренный Э.Г., Дмитриева Е.Н., Ковальчук В.М.,
Коломытцев А.Д. О совершенствовании нормирования качества электроэнергии //
Электричество. - 1987. - №8. - с. 67-69.
2. Куренный Э.Г., Чепкасов Ю.И., Коломытцев А.Д.
Обеспечение достоверности оценок электромагнитной совместимости по
несинусоидальности напряжения // Электромагнитная совместимость:
(Материалы III Республиканской науч.-техн. конференции) - Винница: 1991. -
Вып. 2. - с.135-137.
3. Шидловский А.К., Куренный Э.Г., Коломытцев А.Д.
Статистическая динамика анализаторов гармоник // Техническая электродинамика. -
1983. - №3. - с.3-10.
4. ГОСТ 13109-97. Электрическая энергия.
Совместимость технических средств электромагнитная. Нормы качества электрической
энергии в системах электроснабжения общего назначения. - Введ. в Украине
01.01.2000.
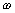 , больших основной
, больших основной 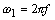 ,
где f=50Гц.
,
где f=50Гц. Можно считать, что ИН не пропускает сигналы с частотой меньшей основной,
а его узкополосные фильтры настроены на частоты
Можно считать, что ИН не пропускает сигналы с частотой меньшей основной,
а его узкополосные фильтры настроены на частоты
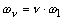 (
(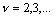 ),
кратные
),
кратные 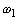 .
То есть, эти фильтры имеют амплитудно-частотные
характеристики (АЧХ) (рис. 1.), максимумы которых
.
То есть, эти фильтры имеют амплитудно-частотные
характеристики (АЧХ) (рис. 1.), максимумы которых
 .
(1)
.
(1)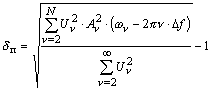

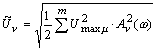 ,
, Перейдем к рассмотрению случайных помех.
В этом случае понятия гармоник не существует, что исключает возможность
применения формул (1-3). Если помеха представляет собой стационарный случайный
процесс с независящими от времени характеристиками, то применительно к
выражению (4) достаточно задать корреляционную функцию
Перейдем к рассмотрению случайных помех.
В этом случае понятия гармоник не существует, что исключает возможность
применения формул (1-3). Если помеха представляет собой стационарный случайный
процесс с независящими от времени характеристиками, то применительно к
выражению (4) достаточно задать корреляционную функцию
