Изменение амплитуды колебаний или волн во времени (в пространстве). Закон изменения в
принципе произволен, однако обычно термин "амплитудная модуляция" применяется к
процессам с медленным (по сравнению с исходными несущими колебаниями) изменением
амплитуд, когда их поведение приближенно можно описать с помощью непрерывных функций (огибающих). Как несущие колебания, так и их огибающие
могут быть гармоническими, импульсными, случайными и т. п., однако
наиболее важны и представительны случаи, когда несущие колебания синусоидальны.
Тогда колебания с амплитудной модуляцией можно представить в виде: ![]() ,
где
,
где ![]() - медленная функция, описывающая поведение
огибающей,
- медленная функция, описывающая поведение
огибающей, ![]() и
и
![]() - частота и начальная фаза исходных колебаний. Условие медленности
изменения амплитуд на характерном временном интервале, равном периоду Т, определяется неравенством
- частота и начальная фаза исходных колебаний. Условие медленности
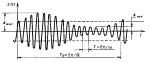
изменения амплитуд на характерном временном интервале, равном периоду Т, определяется неравенством ![]() . В простейшем случае (рис.) изменения огибающей
по синусоидальному закону
. В простейшем случае (рис.) изменения огибающей
по синусоидальному закону ![]() с частотой
с частотой ![]() для характеристики относительного изменения амплитуды модулированных колебаний
используют параметр
для характеристики относительного изменения амплитуды модулированных колебаний
используют параметр ![]() - коэффициент модуляции.
- коэффициент модуляции.
В технике амплитудную модуляцию применяют для передачи информации на
расстояние обычно с помощью электромагнитных волн радио- и оптического диапазонов (хотя существуют системы
передачи с помощью звуковых и других колебаний); суть амплитудной
модуляции - перенос низкочастотного спектра модулирующего (информационного) сигнала в
высокочастотную область, характерную для спектра исходных (несущих энергию)
колебаний. Спектральный состав сигналов с амплитудной модуляцией может быть
довольно сложным. Так, в случае несинусоидальной огибающей по обе стороны от
спектральной линии несущей частоты ![]() возникают полосы спектральных компонент т. н. боковых частот
возникают полосы спектральных компонент т. н. боковых частот ![]() ,
где
,
где ![]() - частота первой гармоники спектра информационного сигнала. Если
спектр боковых частот симметричен относительно
- частота первой гармоники спектра информационного сигнала. Если
спектр боковых частот симметричен относительно ![]() ,
то амплитудная модуляция называется линейной, если несимметричен, то называется
нелинейной. Ширина областей боковых частот должна быть существенно меньше
несущей частоты
,
то амплитудная модуляция называется линейной, если несимметричен, то называется
нелинейной. Ширина областей боковых частот должна быть существенно меньше
несущей частоты ![]() .
Чем уже полоса боковых частот, тем эффективнее решаются задачи
технической реализации приемно-передающих трактов. Полезная информация полностью
содержится в каждой из двух областей боковых частот. Поэтому для информационной
связи достаточно передать лишь одну из боковых полос. В многоканальных системах связи в качестве несущего
сигнала используют негармоническое колебание, а периодическое последовательность
радиоимпульсов.
.
Чем уже полоса боковых частот, тем эффективнее решаются задачи
технической реализации приемно-передающих трактов. Полезная информация полностью
содержится в каждой из двух областей боковых частот. Поэтому для информационной
связи достаточно передать лишь одну из боковых полос. В многоканальных системах связи в качестве несущего
сигнала используют негармоническое колебание, а периодическое последовательность
радиоимпульсов.
Для физики характерна также т. н. естественная амплитудная модуляция колебаний, связанная либо с взаимодействием исходных колебаний с нестационарной средой (в частности, с флуктуациями плотности жидкости или газа, колебаниями кристаллической решетки в твердом теле, см., например, рассеяние Мандельштама-Бриллюэна), либо с реакцией среды на изменение ее параметров под действием исходных колебаний или волн (см., например, Самофокусировка света). Наряду с пространственной самофокусировкой (модуляцией интенсивности излучения) встречаются эффекты самомодуляции (автомодуляции) волн в нелинейных диспергирующих средах, связанные с неустойчивостью плоских гармонических волн по отношению к низкочастотным модулирующим возмущениям, вызывающим амплитудную модуляцию исходных (как волновых, так и автоволновых) колебаний (см. Самомодуляция света). Естественная амплитудная модуляция используется для диагностики параметров разнообразных сред (спектроскопия), формирования мощного светового излучения (нелинейная оптика) и других приложений.