ЗАДАЧА О КАНАЛЕ С ТЕПЛОВЫМ ВОЗДЕЙСТВИЕМ.
СООБЩЕНИЕ 1
Г. Г. Пятышкин, П. П. Киндяков
Донецкий национальный
технический университет
Теплотехнологические агрегаты черной металлургии не только наиболее энергоемкие, но и являются самыми мощными источниками загрязнения окружающей среды (включая и тепловые).
Очевидно, что более совершенные агрегаты имеют относительно высокий КПД, меньше потребляют энергии и меньше выделяют загрязнений.
Одним из факторов, влияющих на эффективность теплового устройства, является интенсивность теплообменных процессов, в том числе и на поверхностях обрабатываемого материала, например, коэффициент теплообмена между рабочей средой и поверхностями.
Элементарным конструктивным элементом, присущим многим теплотехнологическим агрегатам, является труба, внутри которой двигается вязкая среда, а ее поверхность подвергнута тепловому воздействию. На таком элементе относительно легко экспериментировать и выявлять зависимость коэффициента теплообмена от различных факторов.
Поэтому в
настоящей работе формулируется задача в следующей постановке: пусть по трубе
радиусом R двигается теплоноситель, температура которого
в начальный момент времени составляет tНАЧ, а его расход - G [кг/с]. ]. Течение принимается гидродинамически
стабилизировано. В этом случае поперечная скорость Vr = 0, а продольная составляющая скорости Vx не изменяется по длине трубы, а будет изменяться по радиусу, например,
по закону: 
где V0 – скорость на оси трубы;
VCP – средняя скорость по
сечению. VCP = G/(rpR2).
Соотношение между средней и осевой скоростью
определяется выражением:
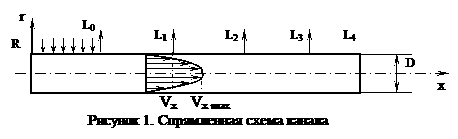Для удобства дальнейшего изложения развернем замкнутый контур (см. рис.
1)
На вертикальном участке L0 происходит внешний нагрев трубы постоянным тепловым потоком q0, на всех остальных участках труба находится в состоянии естественной
конвекции с окружающей средой с температурой tBX. В цилиндрической системе координат уравнение
сохранения энергии в подвижных средах имеет вид:
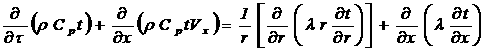(1)
В начальный момент времени теплоноситель
имеет постоянную температуру, т.е. при t= 0; t
= tНАЧ. С некоторого
момента времени t > 0 внешняя
поверхность трубы будет находиться при следующих условиях:
на участке 0 £ x £ L0 – задан греющий
тепловой поток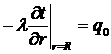
; (2)
на остальных
участках задаются граничные условия 3 – го рода:
для L0 £ x £ L1: 
; (2а)
для L1 < x £ L2: 
; (2б)
для L2 < x £ L3: 
; (2в)
для L3 < x £ L4: 
; (2г)
В этих выражениях aк1, aк2, aк3, aк4 – коэффициенты
теплообмена между цилиндрической стенкой и средой в условиях термогравитационной конвекции. Для их нахождения
используется критериальное уравнение: 
, (3а)
в котором коэффициенты С и n
зависят от изменения числа Релея Ra = PrGr следующим образом:
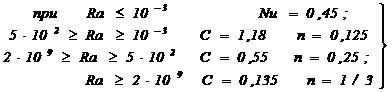(3б)
В качестве характерного размера для
горизонтальной трубы принят ее диаметр, для вертикальной – расстояние от начала
участка до рассматриваемого сечения. Предполагается, что по внешнему контуру
трубы тепловая нагрузка распределена равномерно, поэтому искомое поле
температур не зависит от координаты f, а на оси трубы r
= 0 будет выполняться условие симметрии 
. (4)
В начале трубы (х =
0) и в ее конце (x = Lx) температуры должны
совпадать, так как труба представляет замкнутый контур. После решения задачи,
когда поле температур внутри трубы будет найдено, можно будет найти значение
локальных коэффициентов теплоотдачи от внутренней поверхности трубы к
теплоносителю по следующему выражению: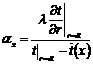 
, где величина t(x) – может быть вычислена как
среднерасходная температура теплоносителя в сечении
Х:
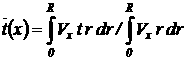(5)
Поставленная
задача часто встречается на практике и является наиболее простой в классе задач
о конвективном теплообмене, так как анализируется уравнение сохранения энергии
в подвижной среде с заданным полем скорости. Детальное изучение процесса
теплообмена планируется выполнить численным экспериментом.
В
предлагаемой работе авторы излагают часть магистерской работы, надеясь обсудить
постановку задачи и учесть высказанные замечания.
В
следующих сообщениях будут изложены методики проведения исследований, блок –
схема алгоритма расчета и анализ полученных результатов.