ЗАДАЧА ПРО КАНАЛ З ТЕПЛОВОЮ ДІЄЮ. ПОВІДОМЛЕННЯ 1

 

Г. Г. П’ятишкін, П. П. Кіндяков

Донецький національний технічний університет

 

Теплотехнологічні агрегати чорної металургії не тільки найенергоємніші, але і є наймогутнішими джерелами забруднення навколишнього середовища (враховуючи і теплові).

Очевидно, що досконаліші агрегати мають відносно високий ККД, менше споживають енергії і менше виділяють забруднень.

Одним з факторів, що впливають на ефективність теплового пристрою, є інтенсивність теплообмінних процесів, у тому числі і на поверхнях оброблюваного матеріалу, наприклад, коефіцієнт теплообміну між робочим середовищем і поверхнями.

Елементарним конструктивним елементом, властивим багатьом теплотехнологічним агрегатам, є труба, усередині якої рухається в'язке середовище, а її поверхня піддана тепловій дії. На такому елементі відносно легко експериментувати і виявляти залежність коефіцієнта теплообміну від різних факторів.

Тому в справжній роботі формулюється задача в наступній постановці: хай по трубі радіусом R рухається теплоносій, температура якого в початковий момент часу складає tНАЧ, а його витрата - G [кг/з]. ]. Течія приймається гидродінамічно стабілізовано. В цьому випадку поперечна швидкість Vr _{= 0, а подовжня} складова швидкості Vx не змінюється по довжині труби, а змінюватиметься по радіусу, наприклад, згідно із законом:                       

де        V₀ – швидкість на осі труби;

            V_CP – середня швидкість по перетину. V_CP = G/(rpR²).

Співвідношення між середньою і осьовою швидкістю визначається виразом:

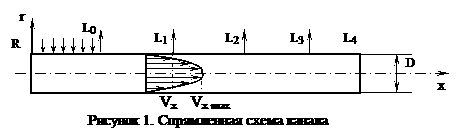Для зручності подальшого викладу розвернемо замкнутий контур (див. рис. 1)

 

 

 

 

 

 

 

На вертикальній ділянці L0 відбувається зовнішній нагрів труби постійним тепловим потоком q0, на всій решті ділянок труба знаходиться в стані природної конвекції з навколишнім середовищем з температурою t_BX. В циліндровій системі координат рівняння збереження енергії в рухомих середовищах має вигляд:

 

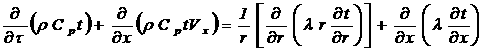        (1)

У початковий момент часу теплоносій має постійну температуру, тобто при t= 0; t = t_НАЧ. З деякого моменту часу t > 0 зовнішня поверхня труби знаходитиметься за наступних умов:

на ділянці 0 £ x £ L0 – заданий гріючий тепловий потік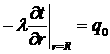;             (2)

на решті ділянок задаються граничні умови 3 – го роду:

  для L0 £ x £ L1:                                ;    (2а)

            для L1 < x £ L2:                                ;   (2б)

  для L2 < x £ L3:                                ;    (2в)

            для L3 < x £ L4:                                ;    (2г)

У цих виразах a_к1, a_к2, a_к3, a_к4 – коефіцієнти теплообміну між циліндровою стінкою і середовищем в умовах термогравітаційної конвекції. Для їх знаходження використовується критерійне рівняння:  ,                     (3а)

у якому коефіцієнти С і n залежать від зміни числа Релея Ra = PrGr таким чином:

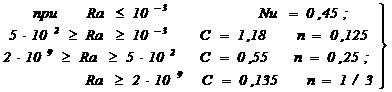         (3б)

Як характерний розмір для горизонтальної труби прийнятий її діаметр, для вертикальної – відстань від початку ділянки до даного перетину. Передбачається, що по зовнішньому контуру труби теплове навантаження розподілено рівномірно, тому шукане поле температур не залежить від координати f, а на осі труби r = 0 виконуватиметься умова симетрії .                                  (4)

На початку труби (х = 0) і в її кінці (x = Lx) температури повинні співпадати, оскільки труба являє собою замкнутий контур. Після рішення задачі, коли поле температур усередині труби буде знайдено, можна буде знайти значення локальних коефіцієнтів тепловіддачі від внутрішньої поверхні труби до теплоносія по наступному виразу:, де величина t(x) – може бути обчислена як середньовитратна температура теплоносія в перетині Х:

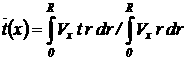                                                (5)

            Поставлена задача часто зустрічається на практиці і є найпростішою в класі задач про конвективний теплообмін, оскільки аналізується рівняння збереження енергії в рухомому середовищі із заданим полем швидкості. Детальне вивчення процесу теплообміну планується виконати чисельним експериментом.

            У пропонованій роботі автори висловлюють частину магістерської роботи, сподіваючись обговорити постановку задачі і врахувати виказані зауваження.

            У наступних повідомленнях будуть висловлені методики проведення досліджень, блок – схема алгоритму розрахунку і аналіз одержаних результатів.