УДК
621.777.001Давиденко А.А. (Донецк, ДонГТУ), Бейгельзимер Я.Е. (Донецк, ДонФТИ)
АНАЛИЗ ОБРАЗОВАНИЯ СВЯЗЕЙ МЕЖДУ СОСТАВЛЯЮЩИМИ
БИМЕТАЛЛА В ПРОЦЕССЕ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
Предложена модель, позволяющая рассчитывать прочность сцепления на сдвиг составляющих биметаллического материала, полученного в процессе совместной пластической деформации разнородных металлов. Модель базируется на пленочной гипотезе схватывания и учитывает шероховатости контактных поверхностей.
Model permitting to calculate the bimetal component shear coupling strength during joint plastic deformation of heterogeneous metals has been proposed. The model is based on film grip hypothesis and takes into account roughness of contact surfaces
.Актуальной задачей при получении слоистых материалов методами ОМД является прогноз прочности соединения составляющих композита. Решение этой задачи позволит более эффективно управлять процессом изготовления слоистых материалов, подбирая оптимальные условия и режимы деформирования. Однако сложность совместной пластической деформации разнородных металлов, недостаточное знание физической природы образования соединения металлов в твердой фазе не позволяют в настоящее время получить универсальную аналитическую зависимость, пригодную для расчетов технологических параметров используемого процесса. Например, для расчета прочности соединения в зависимость должны были бы входить факторы, связанные с природой взаимодействующих материалов, состоянием их контактных поверхностей, скоростью, продолжительностью и температурой взаимодействия, состоянием окружающей среды, геометрическими характеристиками и др. Некоторые из этих факторов влияют не только на прочность соединения, но и сложно взаимодействуют друг с другом.
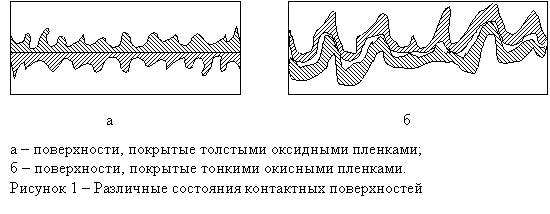
В работе [1] нами была предложена модель, позволяющая прогнозировать прочность соединения составляющих при гидропрессовании биметаллов. Позднее, зависимости, полученные в этой работе, были использованы для расчета прочности соединения на сдвиг компонентов биметаллического прутка, состоящего из массивного железоникелевого сердечника и тонкой медной оболочки. Модель основывалась на пленочной гипотезе схватывания [2], согласно которой образование прочных металлических связей происходит после разрушения оксидных пленок на участках контакта соединяемых материалов, последующего затекания более мягкого металла в образовавшиеся щели и соединения ювенильных поверхностей. В данной модели было принято условие, что поверхности металлов покрыты достаточно толстыми оксидными пленками микронных размеров, сглаживающих собой существующие микронеровности (рис. 1а). Такая ситуация может быть характерна для механически обработанных поверхностей металлов после отжига в атмосферных условиях. Однако довольно часто возникает ситуация, показанная на рис. 1б, когда мы имеем шероховатые поверхности, покрытые тонкими окисными пленками нанометрических размеров. В этом случае при расчете прочности соединения на сдвиг необходимо учитывать механическое зацепление микронеровностей. В настоящей работе мы развиваем модель, позволяющую исследовать процессы схватывания в этих условиях.
В работе [3] показано, что способность материалов к схватыванию определяется в основном их пластичностью, то есть способностью образовывать фактическую площадь контакта. Далее налагаются дополнительные условия: отсутствие или наличие защитных пленок, шероховатость поверхности и др. Однако, необходимо учитывать, что в атмосферных условиях определяющим фактором препятствующем схватыванию металлов является наличие на их поверхностях защитных окисных пленок. В процессе деформации эти пленки разрушаются, однако, если содержание кислорода в газовой среде достаточно велико, то они мгновенно образуются вновь, предотвращая тем самым непосредственный контакт ювенильных металлических поверхностей. Это положение подтверждается работой [4], в которой показано, что в условиях глубокого вакуума сварка давлением происходит при ничтожно малых деформациях, а по мере ухудшения вакуума деформация возрастает. Таким образом, задача, прежде всего, сводится к исследованию процесса формирования фактической площади контакта шероховатых поверхностей.

Существует множество моделей описывающих процесс формирования фактической площади контакта [5] и др., однако все они дают сходную зависимость вид которой:
![]() (1)
(1)
где h
- относительная фактическая площадь контакта;q - нормальное контактное давление;
s s - предел текучести материала;
k1 – коэффициент, зависящий от принимаемых в модели условий.
Из анализа зависимости (1) видно, что с ростом контактного давления, а, следовательно, и деформации растет площадь фактического контакта металлов, что согласно работе [3] должно приводить к росту адгезионного схватывания поверхностей. В реальных условиях холодной пластической деформации и небольших скоростей деформирования, по-видимому, происходит следующее.
В результате пластической деформации соприкасающихся микровыступов и дальнейшего течения более мягкой составляющей происходит разрушение окисных пленок и обнажение ювенильных поверхностей металла, однако, активное воздействие окружающей газовой среды на материал приводит к их регенерации. Так происходит до тех пор, пока поступление молекул газа через зазоры полностью не прекращаются. Далее подвод газа к ювенильным поверхностям затрудняется, и здесь возникают вакуумные условия, которые способствуют образованию металлических связей. Таким образом, первоначальное схватывание происходит на некоторых локальных участках, затем число таких участков увеличивается до образования сплошных зон соединения. Другими словами, фактическая площадь контакта h в процессе своего роста достигает какой-то величины h *, после чего уже не возможна регенерация окисных пленок; дальнейший рост h приводит к образованию оголенных поверхностей, на которых происходит образование металлических связей.
Приблизительную оценку для величины h * можно получить на основе теории перкаляции [6]. Согласно этой теории, при h = 0,5 в контакте начинает образовываться система замкнутых каналов куда уже не проникает воздух. Исходя из этого, в первом приближении можно принять, что h * = 0,5.
Относительную площадь оголенных поверхностей h оп
определим следующим образом: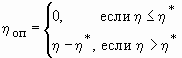 (2)
(2)
Описав, таким образом, схватывание шероховатых металлических поверхностей, перейдем к определению прочности сцепления на сдвиг при гидропрессовании биметаллического прутка. Для этого рассмотрим небольшой участок контакта металлов, образовавшийся в процессе совместной пластической деформации компонентов биметалла (рис. 2).
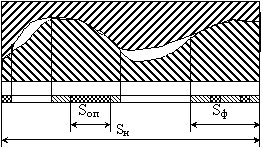
Рисунок 2 – Участок контакта металлов
Силу сцепления на сдвиг Fсц
определим как сумму сил механического зацепления и физического схватывания![]() (3)
(3)
где
t – прочность сцепления на свиг;Sн – номинальная площадь контакта;
Sф – фактическая площадь контакта;
Sоп – площадь оголенных (сварившихся) поверхностей;
kсдв – касательное напряжение на поверхностях сдвига;
kсхв – касательное напряжение на поверхностях схватывания.
Отсюда прочность сцепления на сдвиг определяется как
![]() (4)
(4)
Коэффициенты k
1, kсдв, kсхв определим исходя из следующих соображений.Пусть h оп
= 0, то есть происходит постоянная регенерация окисных пленок, и вкладом отдельных сварившихся участков контакта можно пренебречь, в этом случае имеем простое механическое зацепление микронеровностей: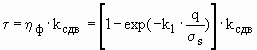 (5)
(5)
Данная зависимость подобна полученной в работе [7] на основе опытных данных:
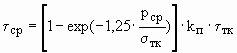 (6)
(6)
где
t ср – среднее напряжение трения;pср – среднее контактное давление;
s тк – предел текучести материала в приконтактном слое;
t тк – предел текучести материала в приконтактном слое при сдвиге;
kп – константа поверхности.
Сопоставляя (5) и (6) видим, что kсдв = kп× t тк, k1 = 1,25.
Физический смысл и численные значения
kп в зависимости от влияния различных факторов представлены в работе [7]. В этой же работе приведены рекомендации по определению механических свойств приконтактного слоя металла s тк и t тк:![]() (7)
(7)
где s т
– предел текучести в объеме металла вблизи контактной поверхности;s тmax – предел текучести предельно упрочненного материала.
В качестве kсхв следует брать, очевидно, какое-то среднее значение между s тк и t тк, поскольку в условиях микронеровностей на межслойной поверхности отрыв по мостикам схватывания может происходить как в нормальных, так и в касательных плоскостях сдвига. Для простоты в качестве kсхв берем величину t тк.
В окончательном виде имеем прочность сцепления на сдвиг:
![]() (8)
(8)
Соотношение (8) совместно с (2) может быть использовано для расчета прочности соединения составляющих биметалла в процессах ОМД.
ПЕРЕЧЕНЬ ССЫЛОК
Давиденко А.А., Орлов Д.В., Сарры Е.А., Бейгельзимер Я.Е. Прогноз прочности соединения составляющих при гидропрессовании биметаллов // Удосконалення процесів та обладнання обробки тиском в
Айнбиндер С.Б. Холодная сварка металлов.- Рига: Изд-во АН Латв.ССР, 1957.- 163 с.
Гегузин Я.Е., Крагельский И.В., Парицкая Л.Н. О взаимном схватывании металлов при высоких температурах под давлением // О природе схватывания твердых тел / М.: Наука, 1968.
Веркин Б.И., Кравченко Е.Л., Люличев А.Н. Исследование адгезионных свойств чистых поверхностей меди и алюминия // О природе схватывания твердых тел / М.: Наука, 1968.
Макушок Е.М., Калиновская Т.В., Белый А.В. Массоперенос в процессах трения. – Минск: Наука и техника, 1978.- 272 с.
Эфрос А.Л. Физика и геометрия беспорядка. М.: Наука, 1982.- 175 с.
Контактное трение в процессах обработки металлов давлением / А.Н. Леванов, В.Л. Колмогоров, С.П. Буркин, Б.Р. Картак и др. - М.: Металлургия, 1976.- 416 с.