Библиотека Статья Карабчевский ВВ Проглядова НЛ Автоматическое решение задач начертательной геометрии

       Начертательная геометрия - одна из сложных дисциплин в техническом вузе, традиционные методы изучения которой все больше заменяются использованием компьютерных технологий.
       В ДонНТУ для обучения начертательной геометрии применяются в основном традиционные методы, но на кафедре ПМИ ДонНТУ лабораторные работы по начертательной геометрии выполняются в системе AutoCAD средствами точного построения [1, 2]. Поставлена задача разработки системы автоматического решения задач начертательной геометрии в среде AutoCADа. Автоматическое решение задач должно быть реализовано как для демонстрации решения, так и для проверки правильности решения при произвольных условиях (как "эталон для сравнения" [1]).
       Отметим, что во многих вузах создаются электронные учебники [2, 3, 4], задачники [5], обучающе-контролирующие программы по курсу начертательной геометрии [6]. Созданные обучающие системы представляют собой самостоятельные графические редакторы, отдельные разработки реализуют демонстрацию решения и проверку правильности построений, однако были созданы для ОС DOS [7].
       Таким образом, разработок по автоматическому решению задач в AutoCAD при поиске в Интернет встречено не было. Особенностью является то, что система AutoCAD позволяет реализовать решение координатно-графическими методами. Удобным инструментом решения служит язык AutoLISP, позволяющий осуществлять операции с графическими объектами AutoCADа [1].
       Поскольку одним и тем же методом можно решать разные задачи (каждая со своими особенностями при разных исходных данных), основы построений конкретным методом могут быть отражены в одном алгоритме. Для автоматизации решения класса задач конкретным методом необходимо выделить общие шаги алгоритмов решения этих задач и определить их реализацию средствами автоматизации.

Решение задач методом вращения вокруг линии уровня

Будем рассматривать метод вращения вокруг линии уровня для решения следующих метрических задач:

       Рассмотрим решения задач вращением вокруг горизонтали (вращение вокруг фронтали выполняется аналогично).
       Начнем рассмотрение задачи определения натуральной величины треугольника (задача 2). Исходные данные задачи: координаты трех точек А (ax, ay, az), В (bx, by,bz), С (cx, cy, cz). Постановка задачи подразумевает построение фронтальной и горизонтальной проекций треугольника. Фронтальные проекции точек А, В и С обозначаются соответственно А2, В2, С2 и имеют координаты: А2 (ах, az), В2 (bx, bz), С2 (сx, сz). Горизонтальные проекции точек А, В и С обозначаются соответственно А1, В1 и С1 и имеют координаты: А1 (ах, ay), В1 (bx, by), С1 (cx, cy). Заметим, что для построения эпюра в AutoCAD необходимо учитывать направление осей координат в системе.
       Последовательность решения задачи (рис. 1):

       1. Проводим проекции горизонтали h. Заметим, что удобно проводить горизонталь из "средней" (по координате y фронтальной плоскости) точки, поскольку в этом случае нет необходимости продлевать стороны треугольника до пересечения с горизонталью [1].
       2. Построение перпендикуляров к фронтальной и горизонтальной проекции горизонтали треугольника, опущенных из соответствующих проекций вершин треугольника (кроме "средней" точки C2).
       3. Построение отрезков длинами перпендикуляров, опущенных из фронтальных проекций двух вершин треугольника (кроме "средней") к фронтальной проекции горизонтали, параллельно горизонтальной проекции горизонтали из соответствующих горизонтальных проекций точек.
       4. Построение радиусов вращения вершин треугольника в натуральную величину. Радиусы вращения находятся по правилу прямоугольного треугольника.
       5. Построение повернутых вокруг горизонтали проекций вершин треугольника (кроме "средней", которая принадлежит горизонтали и не подвижна). Искомые проекции вершин, повернутых вокруг горизонтали, А1' и B1' будут лежать на перпендикуляре к горизонтали (перпендикуляры являются следами их вращения).
       6. Построение сторон треугольника натуральной величины осуществляется соединением полученных проекций точек треугольника между собой.

Электронная библиотека

АВТОМАТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Карабчевский В.В., Проглядова Н.Л.

	Электронная библиотека по теме: "Автоматическое решение задач начертательной геометрии"
	АВТОМАТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ (Тезисы статьи, подготовленной к публикации в сборник "Научные труды Донецкого национального технического университета" за 2004 г.) Карабчевский В.В., Проглядова Н.Л. tashka_pl@ua.fm Введение Начертательная геометрия - одна из сложных дисциплин в техническом вузе, традиционные методы изучения которой все больше заменяются использованием компьютерных технологий. В ДонНТУ для обучения начертательной геометрии применяются в основном традиционные методы, но на кафедре ПМИ ДонНТУ лабораторные работы по начертательной геометрии выполняются в системе AutoCAD средствами точного построения [1, 2]. Поставлена задача разработки системы автоматического решения задач начертательной геометрии в среде AutoCADа. Автоматическое решение задач должно быть реализовано как для демонстрации решения, так и для проверки правильности решения при произвольных условиях (как "эталон для сравнения" [1]). Отметим, что во многих вузах создаются электронные учебники [2, 3, 4], задачники [5], обучающе-контролирующие программы по курсу начертательной геометрии [6]. Созданные обучающие системы представляют собой самостоятельные графические редакторы, отдельные разработки реализуют демонстрацию решения и проверку правильности построений, однако были созданы для ОС DOS [7]. Таким образом, разработок по автоматическому решению задач в AutoCAD при поиске в Интернет встречено не было. Особенностью является то, что система AutoCAD позволяет реализовать решение координатно-графическими методами. Удобным инструментом решения служит язык AutoLISP, позволяющий осуществлять операции с графическими объектами AutoCADа [1]. Поскольку одним и тем же методом можно решать разные задачи (каждая со своими особенностями при разных исходных данных), основы построений конкретным методом могут быть отражены в одном алгоритме. Для автоматизации решения класса задач конкретным методом необходимо выделить общие шаги алгоритмов решения этих задач и определить их реализацию средствами автоматизации. *Решение задач методом вращения вокруг линии уровня* Будем рассматривать метод вращения вокруг линии уровня для решения следующих метрических задач: - определение натуральной величины отрезка (задача 1); - определение натуральной величины треугольника (задача 2); - определение величины угла между двумя прямыми (задача 3); - определение расстояния между двумя параллельными прямыми (задача 4). Рассмотрим решения задач вращением вокруг горизонтали (вращение вокруг фронтали выполняется аналогично). Начнем рассмотрение задачи определения натуральной величины треугольника (задача 2). Исходные данные задачи: координаты трех точек А (ax, ay, az), В (bx, by,bz), С (cx, cy, cz). Постановка задачи подразумевает построение фронтальной и горизонтальной проекций треугольника. Фронтальные проекции точек А, В и С обозначаются соответственно А2, В2, С2 и имеют координаты: А2 (ах, az), В2 (bx, bz), С2 (сx, сz). Горизонтальные проекции точек А, В и С обозначаются соответственно А1, В1 и С1 и имеют координаты: А1 (ах, ay), В1 (bx, by), С1 (cx, cy). Заметим, что для построения эпюра в AutoCAD необходимо учитывать направление осей координат в системе. Последовательность решения задачи (рис. 1): 1. Проводим проекции горизонтали h. Заметим, что удобно проводить горизонталь из "средней" (по координате y фронтальной плоскости) точки, поскольку в этом случае нет необходимости продлевать стороны треугольника до пересечения с горизонталью [1]. 2. Построение перпендикуляров к фронтальной и горизонтальной проекции горизонтали треугольника, опущенных из соответствующих проекций вершин треугольника (кроме "средней" точки C2). 3. Построение отрезков длинами перпендикуляров, опущенных из фронтальных проекций двух вершин треугольника (кроме "средней") к фронтальной проекции горизонтали, параллельно горизонтальной проекции горизонтали из соответствующих горизонтальных проекций точек. 4. Построение радиусов вращения вершин треугольника в натуральную величину. Радиусы вращения находятся по правилу прямоугольного треугольника. 5. Построение повернутых вокруг горизонтали проекций вершин треугольника (кроме "средней", которая принадлежит горизонтали и не подвижна). Искомые проекции вершин, повернутых вокруг горизонтали, А1' и B1' будут лежать на перпендикуляре к горизонтали (перпендикуляры являются следами их вращения). 6. Построение сторон треугольника натуральной величины осуществляется соединением полученных проекций точек треугольника между собой. Рисунок 1 - Построение треугольника натуральной величины Несложно понять принцип решения других задач данным методом. Решение задачи определения натуральной величины отрезка (задачи 1) показано на рис. 2. Исходные данные задачи 1: координаты двух точек А (ax, ay, az) и В (bx, by,bz). Рисунок 2 - Нахождение натуральной величины отрезка Решение задачи определения величины угла между двумя прямыми ( задачи 3) представлено на рис. 3. Исходные данные задачи 3: координаты трех точек А (ax, ay, az), В (bx, by,bz), С(cx, cy, cz), таких что АВС - искомый угол между прямыми а (AB) и b (BC). При решении задачи 3 проводится поворот вершины угла вокруг горизонтали до положения, когда плоскость угла станет параллельной горизонтальной плоскости. Решение задачи определения расстояния между двумя параллельными прямыми (задачи 4) показано на рис. 4. Исходные данные: координаты точек А (ax, ay, az), В (bx, by,bz), С(cx, cy, cz), D (dx, dy, dz), определяющих прямые АВ (a) и СD (b). 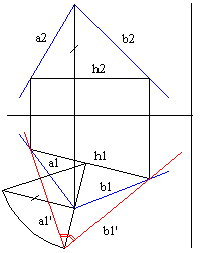Рисунок 3 - Определение величины угла между двумя прямыми Рисунок 4 - Определение расстояния между двумя параллельными прямыми Алгоритм автоматического решения задач Выделим шаги алгоритма автоматизации решений рассмотренных задач. 1. Постановка задачи. Описание данных множествами позволит легко перейти к реализации на языке AutoLisp, оперирующем со списками. Исходные данные представим в виде множества из четырех точек. Точка - множество из элементов-координат. Число точек определяется конкретной задачей: для задачи 1 равно двум, задачи 2 - трем и т.д. Можно считать "отсутствующие" элементы-множества в множестве Исх_данные пустыми. Для постановки задачи строятся множества точек фронтальной и горизонтальной проекции. Таким образом, имеем следующие множества: Исх_данные = {Xi : Xi - Точка3D}=(A, B, C, D) Точка3D ={ (x, y, z) : x, y, z є R} Гориз_проекция = {Xi : Xi - Точка2D}=(A2, B2, C2, D2) Фронт_проекция = {Xi : Xi - Точка2D}=(A1, B1, C1, D1) Точка2D ={ (x, y) : x, y є R}, R - множество действительных чисел Используя значения элементов этих множеств, выполняются построения осей координат и исходных данных задачи в виде эпюра. 2. Построение горизонтали. Для построения горизонтали необходимо выбрать, через какую точку (из исходных) ее лучше провести. Горизонталь = { (hi1, hi2) : hi1, hi2 - Точка2D } = (h1, h2). Далее элементы множеств Гориз_проекция и Фронт_проекция упорядочиваются, например, по возрастанию z-координаты. С помощью функции list в Автолиспе создаются списки, с помощью функции setq они сохраняются в переменную. В соответствии с описанием множествами можно сказать, что setq определяет новое множество. 3. Проведение перпендикуляров. Для задачи 1 этот шаг пропускается. 4. Построение параллельных отрезков. 5. Построение радиуса вращения. 6. Определение повернутых вокруг горизонтали проекции вершин. Повернутые проекции вершин (кроме лежащей на горизонтали) будут лежать на перпендикуляре, проведенном из данной вершины к горизонтальной проекции горизонтали, на расстоянии радиуса вращения. Выводы Изучив ход построений решения задач (одного класса) методом вращения вокруг линии уровня удалось выделить общие шаги построений для реализации алгоритма их автоматического решения координатно-графическими методами. Автоматическое решение задач с помощью языка AutoLisp в среде AutoCAD производится с помощью набора специальных функций. Дальнейшие усилия будут направлены на исследование особенностей построений при решении задач этого же класса методом замены плоскостей проекций и разработку общего алгоритма автоматического решения. Литература Карабчевский В.В. Автоматическая генерация решения задач начертательной геометрии как средство формирования эталонов в подсистеме тестирования. // Научные труды Донецкого национального технического университета. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2002). Выпуск 52: Донецк: ДонНТУ, 2002. - 248 с. Карабчевский В. В. Мультимедийный учебник по начертательной геометрии. // Образование и виртуальность-2002. Сборник научных трудов 6-й Международной ВИРТ-2003 конференции Украинской ассоциации дистанционного образования. Харьков-Ялта:УАДО, 2002.- С. 198 - 203. О применении мультимедийных средств в начертательной геометрии. Толстихин С.А. // Красноярский государственный технический университет. www.nspu.net/tolstihin.doc Компьютерный конспект лекций по начертательной геометрии. Швайгер А.М. // Южно-Уральский государственный университет. 2000. http://www.informika.ru/text/database/geom/Geometry/ALEXANDR.HTML Иванов А.В., Родионов В.В., Лысенко К.Н., Бочков А.М. Электронный задачник по начертательной геометрии. Пензенский технологический институт. http://www.nocnit.ru/2st/materials/ivanov.html. Обучающе-контролирующий программный комплекс по курсу "Начертательная геометрия". Юсупова М.Ф. // Одесский Национальный Морской Университет. Кафедра начертательной геометрии и инженерной графики. http://www.osmu.odessa.ua/index.php?kafedr_ngig_work Кисляков В.В., Осовец С.В. Программный комплекс для постановки и решения задач по начерательной геометрии. ОТИ МИФИ. Электронная конференция ЭНИТ-2000, 17-19 мая, Ульяновск (Россия). http://enit.ulsu.ru/d/003/.