АВТОМАТИЧЕСКАЯ ГЕНЕРАЦИЯ РЕШЕНИЯ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ КАК СРЕДСТВО ФОРМИРОВАНИЯ ЭТАЛОНОВ В ПОДСИСТЕМЕ ТЕСТИРОВАНИЯ

Карабчевский В.В.

       Abstract

       Karabchevsky V.V. Automatic generation of solutions for the tacks of descriptive geometry as means of forming the etalons in testing subsystem. The algorithm of automatic generation of solutions the tacks of descriptive geometry in AutoCAD environment is described. It may be applied for use in teaching systems.

       Введение

       Ни у кого не возникает сомнения в необходимости широкого внедрения компьютерного черчения в учебный процесс. Следует заметить, что для обучения начертательной геометрии применяются в основном традиционные методы, но на кафедре ПМИ ДонНТУ лабораторные работы по начертательной геометрии выполняются только в системе AutoCAD. Такой подход требует развития соответствующего методического обеспечения.
       На кафедре ПМИ разрабатывается дистанционный электронный учебник по курсу "Инженерная графика" [1,2]. В состав учебника входят указания по применению системы AutoCAD для выполнения лабораторных работ. Кроме того, учебник предлагает теоретический материал в виде высококачественных статических и анимированных изображений и содержит ссылку на подсистему графического решения задач начертательной геометрии, поддерживающую соответствие между объектами на эпюре Монжа и их аксонометрическим представлением [3,4]. Для проверки правильности решения при произвольных условиях необходимы средства автоматического решения задачи, такое решение могло бы служить эталоном для сравнения. Разработка таких средств требует соответствующего инструментария. Удобным инструментом решения задачи может служить язык AutoLISP, позволяющий осуществлять операции с графическими объектами AutoCADа. Можно поставить задачу разработки системы, позволяющей автоматически решать задачи начертательной геометрии в среде AutoCADа. Такая система может быть использована как автономно от электронного учебника, так и в составе единого комплекса. Разработанные для нее алгоритмы могут быть в дальнейшем адаптированы для применения в составе дистанционной обучающей среды.

       1. Алгоритм тестирования

       В обучающих системах применяются в основном методы тестирования с закрытой формой ответа и с конструируемым ответом. Желание проверить является ли решение, полученное для произвольных, неизвестных разработчикам системы данных, верным, ведет либо к необходимости отслеживания действий пользователя, либо к анализу графической базы данных. Второй путь показался более простым, кроме того, AutoCAD позволяет решать даже простые задачи различными методами. Состав команд и порядок их применения могут зависеть от стиля работы пользователя. Существует возможность отменять ошибочные действия или удалять результаты неверных построений.
       Попробуем применить этот подход к проверке решения задачи о построении перпендикуляра к плоскости, заданной треугольным отсеком. Заметим, что эта задача не имеет однозначного графического решения. Чертеж может иметь различный вид в зависимости от выбранного для работы места на плоскости XY, различное положение линий уровня влияет на длину отрезков, отображающих фронтальную и горизонтальную проекции перпендикуляра. Однако же можно выделить признаки, однозначно определяющие правильное решение:
              - один из концов перпендикуляра из точки к плоскости инцидентен этой точке;
            - ориентация проекций перпендикуляра (угол наклона к горизонтали) соответствует результатам правильного построения (не зависит от последовательности решения, выбора линии уровня, индивидуального стиля работы с системой AutoCAD).
       Одновременное наличие этих признаков, является условием правильности решения. На основании вышеизложенного может быть построен алгоритм тестирования:

       2. Реализация алгоритма автоматической генерации решения

       На первом этапе следует запросить точку пересечения осей на эпюре Монжа. Это необходимо для приведения координат объектов в соответствие с этой точкой, принимаемой в качестве начала координат при решении задачи. С помощью команды ucsicon отключается отображение пиктограммы системы координат, с помощью команды ucs задается пользовательская система координат с началом в этой точке. Далее следует отключить привязки, чтобы исключить их влияние. Затем (при необходимости) вводятся координаты 4 точек (A,B,C,D). После этого, определим координаты проекций точек. Сформируем списки точек, составляющих горизонтальную и фронтальную проекции треугольника.
       Упорядочим списки по убыванию координаты z (y в системе координат AutoCADа) для точек фронтальной проекции. Из средней точки удобно строить фронтальную проекцию горизонтали, этот подход исключает необходимость удлинения сторон (рис. 1). Пунктиром на рисунке показано построение фронтальной проекции горизонтали из другой точки. Таким же образом построена горизонталь на рис. 2.

Рисунок 1. Построение фронтальной проекции горизонтали

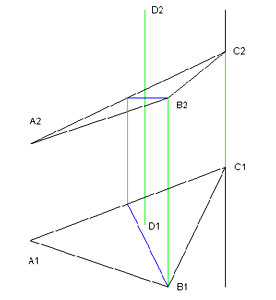
Рисунок 2. Фронтальная и горизонтальная проекция горизонтали

       Упорядочивать будем методом пузырька, адаптированным для трех элементов:
       1. Сравниваем первый со вторым, если нужно - меняем их местами;
       2. Сравниваем второй с третьим, если нужно - меняем их местами;
       3. Сравниваем первый со вторым, если нужно - меняем их местами.
       В качестве иллюстрации приведем результаты решения для данных:
       A(85,42,0); B(25,62,20); C(0,10,40); D(35,35,58). Для наглядности расчеты сопроводим построением.
       С помощью функции inters находим точку пересечения горизонтального отрезка, проходящего из средней точки с противоположной стороной треугольного отсека; эти точки определяют фронтальную проекцию горизонтали (рис. 2). Горизонтальная проекция горизонтали определяется горизонтальной проекцией средней точки и точкой пересечения вертикальной линии, проходящей через точку пересечения фронтальной проекции горизонтали с противоположной стороной треугольного отсека с горизонтальной проекцией этой стороны (рис. 2).
       Найдем перпендикуляр к горизонтальной проекции горизонтали, проходящий через точку D1. Направление перпендикуляра определим путем построения такого отрезка, у которого разность координат Y равна разности координат X горизонтальной проекции горизонтали, а разность координат X равна разности координат Y горизонтальной проекции горизонтали, взятой с обратным знаком. С помощью функции inters определим точку его пересечения с горизонтальной проекцией горизонтали.
       Таким образом, определена горизонтальная проекция перпендикуляра (рис. 3)

Рисунок 3. Горизонталь и горизонтальная проекция перпендикуляра

       Аналогичным образом строится фронталь и фронтальная проекция перпендикуляра (рис. 4).

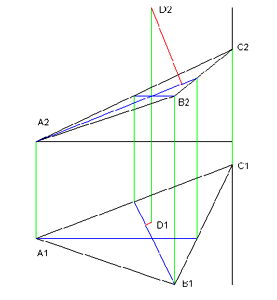
Рисунок 4. Фронталь и фронтальная проекция перпендикуляра.

       3. Реализация проверки результатов решения

       По окончании построения (вернее расчета точек, соответствующих построению) запрашивается фронтальная проекция перпендикуляра.
       Функция entsel позволяет получить список, содержащий имя примитива, указанного пользователем в ответ на запрос.
       С помощью функции entget из базы данных AutoCADа извлекается список свойств этого примитива. Функции assoc и cdr позволяют найти в этом списке тип примитива. Если это отрезок (тип "LINE"), то в списке находятся координаты его начала и конца. Если примитив не является отрезком, выдается сообщение "Указанный объект не является отрезком".
       Далее таким же образом указывается горизонтальная проекция перпендикуляра. Для сравнения результата, полученного пользователем, с результатами расчета, следует откорректировать значения точек, задающих начала и концы отрезков, указанных пользователем, с учетом положения начала координат на эпюре Монжа. Это необходимо, т.к. данные о примитивах хранятся в мировой системе координат, начало координат на эпюре Монжа может быть произвольно расположено на плоскости XY мировой системы координат.
       Проверим, имеет ли указанный пользователем в качестве фронтальной проекции перпендикуляра отрезок начало или конец, совпадающие с точкой D2. Если да, то упорядочим точки, определяющие отрезок, так чтобы начало отрезка совпадало с точкой D2. В противном случае будет выдано сообщение "фронтальная проекция указанного отрезка не исходит из точки D".
       В случае если указанный отрезок исходит из точки D, остается проверить его направление. Это можно сделать, применив функцию inters для отыскания точек пересечения отрезков, указанных пользователем, с отрезками, полученными в результате расчета. В случае совпадения направления отрезков (частный случай параллельности) точка пересечения не находится, функция inters возвращает nil. Если эта ситуация имеет место для фронтальной и горизонтальной проекций, выдается сообщение "задача решена правильно". В противном случае выдается сообщение "указанный отрезок не является перпендикуляром к плоскости".

       Выводы

       Подсистема, выполняющая автоматическую генерацию ответа и предусматривающая его использование в качестве эталона при проверке результатов работы обучаемого, может быть использована при изучении отдельных разделов начертательной геометрии как для самопроверки в ходе самостоятельной работы, так и для тестирования знаний. При этом повышается достоверность результатов, так как обучаемые не будут иметь возможности заранее узнать условие задачи, найти способ угадывания ответа или иным образом обмануть систему. Кроме того, разработчики будут избавлены от необходимости многократно решать задачу для широкого набора исходных данных, что неизбежно при отсутствии возможности автоматического решения.

       Литература

1. Карабчевский В.В. Электронный учебник по курсу инженерная графика // Труды конференции "Информационные технологии в науке, образовании, телекоммуникации, бизнесе". Ялта-Гурзуф, 20-30 мая 2002 года. - С. 285- 287.
2. Карабчевский В.В. Мультимедийный учебник по начертательной геометрии // Образование и виртуальность-2002. Сборник научных трудов 6-й Международной конференции Украинской ассоциации дистанционного образования. Харьков-Ялта: УАДО, 2002. - С. 198-203.
3. Карабчевский В.В. Повышение качества преподавания инженерной графики путем разработки и применения обучающих систем. Научные труды Донецкого государственного технического университета. Серия: Информатика, кибернетика и вычислительная техника, (ИКВТ-99) выпуск 6:-Донецк: ДонГТУ, 1999. - С. 294-299.
4. Карабчевский В.В. Дистанционные технологии в преподавании графических дисциплин // Сборник трудов 5-й Международной конференции "Образование и виртуальность-2001". Харьков-Ялта: УАДО, 2001. - С. 23-28.