Системы обнаружения аномалий: новые идеи в защите информации
Андрей Беляев, Сергей Петренко,
"Экспресс-Электроника"#2/2004
Понятие "обнаружение аномалий" возникло сравнительно недавно и сразу привлекло внимание специалистов в области сетевой безопасности. В середине 2003 года на рынке средств защиты информации появились первые западные и отечественные системы обнаружения аномалий, а поставщики услуг сетевой безопасности начали активно предлагать соответствующие решения. Согласно прогнозам Gartner, 85% крупнейших международных компаний с вероятностью 0.8 воспользуются к 2007 году функциями современных систем обнаружения аномалий. На каких инженерных принципах базируются эти перспективные системы? Какие методики и алгоритмы обнаружения аномалий могут быть полезны для практики отечественных служб защиты информации? Давайте посмотрим вместе.
С завидным постоянством тема обнаружения аномалий возглавляет списки и рейтинги наиболее актуальных проблем в различных федеральных и коммерческих целевых программах в области защиты информации. Так, например, в разработанном Научно-техническим советом НАТО ранжированном списке из 11 важнейших технических задач на период 2002-2007 гг. три первые ориентированы на разработку аппаратных и аппаратно-программных систем обнаружения аномалий вычислительных процессов в современных и перспективных распределенных вычислительных системах на основе TCP/IP. Актуальность этой задачи объясняется тем, что согласно стратегическим отчетам НАТО существующие системы обнаружения вторжений (IDS) ежедневно обнаруживают в среднем 400-600 попыток несанкционированного автоматического вторжения. При этом эксперты подчеркивают: данное число составляет не более 14-17% от общего числа реально осуществляемых атак и воздействий нарушителей. По понятным причинам эти факты настораживают и вызывают определенное беспокойство у специалистов в области защиты информации.
Более того, до сих пор считалось, что относительно просто решается лишь проблема обнаружения вторжений в сетях TCP/IP, которая сводится к задачам распознавания:
- структурных признаков (сигнатур) известных типов атак (S. Kumar, K. Ilgun, P.A. Porras, M. Sebring, T.F. Lunt, R. Jagannathan, T.D. Garley);
- инвариантных признаков структуры корректных вычислительных процессов (E. Eskin, H.S. Javitz, A. Valdes, S. Kumar, T.F. Lunt, R. Jagannathan, T.D. Garley);
- корреляционных признаков нормального функционирования распределенных вычислительных систем (H.S. Javitz, A. Valdes, P. Helman, J. Bhangoo, L. Portnoy, S. Forrest).
Однако в случае задачи распознавания аномалий вычислительных процессов возникает целый ряд затруднений, связанных, главным образом, с необходимостью учета и обнаружения ранее неизвестных типов атак и воздействий. Это предполагает:
- построение некоторого эталонного множества инвариантов нормального (семантически корректного) развития вычислительных процессов в условиях априорной неопределенности воздействий внешней и внутренней среды;
- установление шкал измерения признаков эталонов или инвариантов;
- выявление необходимых и достаточных информативных признаков инвариантов;
- построение правил распознавания аномалий.
Поэтому существующие до сих пор решения отдельных простейших частных случаев решения задачи распознавания аномалий вычислительных процессов (S. Kumar, M. Sebring, T.F. Lunt, R. Jagannathan, T.D. Garley, H.S. Javitz, A. Valdes, P. Helman, J. Bhangoo, L. Portnoy, S. Forrest) не позволили разработать некоторый единый, универсальный метод обнаружения ранее неизвестных типов атак и воздействий (см. табл. 1). Для выполнения этой задачи западные и отечественные научно-исследовательские коллективы и школы срочно занялись углубленной теоретической проработкой данного вопроса.
Таблица 1. Сравнение известных типов систем обнаружения вторжений
| Характеристика | Поиск сигнатур |
Поиск аномалий | |
| Модельпотока | Модельсистемы | ||
| Множество обнаруживаемых атак | априорно задано, ограничивается известными моделями атак | вариативно, достаточно широко | вариативно, максимально широко |
| Вероятность ложного срабатывания | близка к нулю | высока | близка к нулю |
| Вероятность пропуска атаки | средняя | средняя | средняя |
| Требования к вычислительнымресурсам | средние | низкие | высокие |
Не осталась в стороне и российская школа сетевой безопасности. Например, Санкт-Петербургская Школа защиты информации профессора В. В. Ковалева (авторы являются учениками и последователями этой школы), предложила оригинальный способ решения задачи обнаружения аномалий на основе инвариантов подобия. В результате были выработаны принципиально новые инженерные принципы разработки промышленных и коммерческих прототипов систем обнаружения аномалий, которые позволяют теоретически обнаруживать и парировать все виды внутренних и внешних воздействий (в том числе и ранее не известные). Давайте рассмотрим основные идеи этого подхода.
Немного теории обнаружения аномалий
Рассмотрим оператор присваивания
 |
1 |
Для семантически корректного вычислительного процесса в контексте данного оператора должны выполнятся следующие соотношения между абстрактными размерностями параметров (A, B, C, D, E, CONST_1):
 |
2 |
Эти соотношения, так называемые инварианты подобия, позволяют однозначно определить эталон "правильного" функционирования некоторой распределенной вычислительной системы. При этом вычислительный процесс семантически корректен, если соответствующая система уравнений размерностей имеет среди множества векторов-решений хотя бы один, состоящий из всех ненулевых компонент. Действительно, предположим, что, это не так, и среди параметров вычислительного процесса определенной размерности появился параметр тождественно равный нулю при любых значениях других параметров. Это указывает на безразмерность нового параметра. Однако это невозможно, так как противоречит исходному условию определения размерностей параметров вычислительного процесса.
В результате становится возможным предложить универсальную методику обнаружения аномалий на основе инвариантов подобия. Основная идея этой методики заключается в распознавании аномалий вычислительных процессов с помощью сравнения значений инвариантов подобия реальных вычислительных процессов с эталонными значениями инвариантов. К достоинствам методики относится то, что удалось явно исключить шаг выделения независимых параметров вычислительного процесса на основе эвристических алгоритмов. Использование достаточно строгого требования отличия компонент вектора решения от нуля позволило разработать полностью автоматический детерминированный алгоритм обнаружения аномалий. В частности, для вывода инвариантов подобия семантически корректного вычислительного процесса необходимо построить матрицу R-вида:
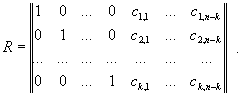 |
3 |
или
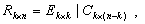 |
4 |
где E - единичная матрица, k и n - количество строк и столбцов исходной матрицы коэффициентов размерностей S соответственно.
Для построения матрицы R достаточно воспользоваться следующими операциями:
- сложение произвольной строки матрицы с линейной комбинацией других строк;
- перестановка строк;
- перестановка столбцов.
Метод построения матрицы R аналогичен методу Жордана-Гаусса, но при этом обладает следующими особенностями. Во-первых, осуществляется двойной обход алгоритма: сначала в прямом (сверху вниз), а затем в обратном (снизу вверх) направлении. Во-вторых, перестановка столбцов производится в тех случаях, когда ненулевое значение ячейки в пределах первых k столбцов (являющееся не первым ненулевым по счету в строке) невозможно привести к нулю из-за отсутствия в данном столбце иных ненулевых членов.
Заметим, что матрица R идентична матрице S за исключением возможных перестановок столбцов, то есть справедливо выражение
 |
5 |
где T - квадратная перестановочная матрица размерности nґn, соответствующая выполненным на этапе построения R перестановкам столбцов в S. Данный результат обусловлен характером специфичных для предметной области преобразований, выполняемых над матрицей S в процессе построения матрицы R.
Таким образом, выражение (5) позволяет использовать матрицу R вместо матрицы S для вывода инвариантов подобия семантически корректных вычислительных процессов в распределенных вычислительных системах на основе TCP/IP. Для наличия среди первых k значений вектора-решения системы ограничений размерности i-й компоненты, тождественно равной нулю, необходимо и достаточно, чтобы в i-й строке матрицы C в формуле (4) все элементы были равны нулю. Действительно, пусть в i-й строке матрицы C существует хотя бы один ненулевой элемент (например, в позиции j ). Тогда, установив равными нулю все (n-k) последних переменных за исключением (k+j)-й, получим следующее равенство:
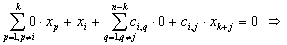 |
6 |
из которого следует, что в данном случае переменная xi не равна нулю. При равенстве нулю всех элементов i-й строки матрицы C получаем следующее равенство:
 |
7 |
из которого получаем искомое тождество:
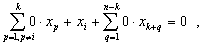 |
8 |
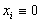 |
9 |
Переменные, соответствующие первым k столбцам матрицы R, являются базисными (независимыми) в данной системе инвариантов подобия (размерностей). Переменные, соответствующие остальным столбцам матрицы R, - зависимые. Таким образом, предлагаемая методика (с полным построением матрицы R) представляет собой единую, универсальную методику обнаружения аномалий вычислительных процессов в распределенных вычислительных системах на основе TCP/IP. Отметим некоторые особенности предлагаемой методики. На практике возможна некоторая модификация методики, в частности, вариация алгоритма построения матрицы R. Например, выделение базисных переменных и необходимые вычислительные преобразования над R производятся при добавлении к ней каждой новой строки. Цель модификации - формирование на каждом шаге анализа матрицы ограничений размерности, приведенной к виду (3).
Данный алгоритм позволяет:
- полностью исключить вычислительные расходы, связанные с поздней (согласно алгоритму Жордана-Гаусса) перестановкой столбцов матрицы;
- уменьшить количество вычислительных операций в ходе выделения единичной матрицы в левой части матрицы R.
Алгоритм требует дополнительного хранения перестановочной матрицы T на всем этапе контроля семантической корректности вычислительного процесса, что несколько замедляет доступ к элементам матрицы. Однако использование эффективных структур данных позволяет свести дополнительные расходы к минимуму.
Отметим, построение матрицы R в ходе контроля семантической корректности вычислительного процесса позволяет обнаружить семантическую ошибку до окончания всего построения (однако вовсе не обязательно, что критерий корректности нарушится именно в момент добавления информации об ошибочной строке процесса). Данный факт является определенным достоинством предлагаемой инженерной методики обнаружения аномалий в случае наличия в сети передачи данных большого количества ошибочных пакетов (умышленно либо неумышленно порожденных). В этом случае станция-получатель L, еще не декодировав сообщение полностью, может принять решение об его игнорировании. Данную особенность можно использовать при создании комплексной системы защиты от атак класса "отказ в обслуживании". При этом в нормальных условиях функционирования досрочные отклонения пакетов не влияют на среднестатистическую вычислительную трудоемкость. В связи с тем, что доля аномальных реализаций процессов стека сетевых протоколов стремится к нулю.
Другая особенность рассмотренной методики - наличие нескольких независимых между собой групп размерностей переменных. Примером могут служить счетчики, обрабатываемые данные, сетевые адреса, параметры протоколов. В результате, почти для всех сетевых протоколов множество параметров можно разбить на подмножества общим числом от 2 до 5-10, в зависимости от специфики протокола. Аналогами данных подмножеств в пространстве образов отображения ? являются связные компоненты графа. Внутри каждого подмножества аналогично основному множеству можно выделить базисные и зависимые переменные. Отмеченная особенность позволяет с минимальными вычислительными затратами привести матрицу S путем перестановки строк и столбцов к блочно-диагональному виду:
 |
10 |
Дальнейшая обработка матрицы S может производиться независимо для каждой из матриц S'i . При этом алгоритм построения матрицы вида (6) может применяться независимо к каждой из матриц S'i . В таком случае общий вид матрицы S имеет вид:
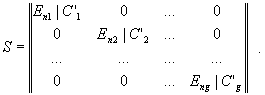 |
11 |
Причем если хотя бы для одной из матриц С'i не выполняется условие, справедливое для матрицы С в целом, то это говорит об аномалии вычислительного процесса и наличии семантической ошибки.
Оценка вычислительной трудоемкости предлагаемой методики
Для системы n уравнений с n неизвестными при отсутствии выборок из массива (хранящего информацию о перестановках строк и столбцов) общая вычислительная трудоемкость вывода инвариантов подобия равна количеству операций процессора
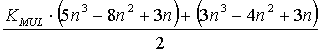 |
12 |
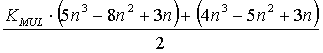 |
13 |
Здесь KMUL - коэффициент вычислительной трудоемкости операции целочисленного умножения по сравнению с операцией целочисленного сложения для данной аппаратной платформы. Например, для процессоров класса Intel Pentium значение этого коэффициента составляет 6-10 раз, для процессоров класса Intel 8086 может достигать 20-40 раз. При возможности реализации кэширования с высокой частотой попадания в кэш значение KMUL снижается до 2 раз.
Как следствие, выигрыш в вычислительной трудоемкости выделения инвариантов подобия в основном зависит от пропорций разбиения матрицы S на независимые компоненты. Так, например, при расслоении множества переменных на g подмножества равной мощности выигрыш K в вычислительной трудоемкости можно рассчитать по формуле:
 |
14 |
При этом выигрыш будет больше единицы при любом значении
g  2 и KMUL
2 и KMUL  2. В случае неравномерного разбиения множества переменных оценку
полученного выигрыша можно рассчитать следующим образом. Пусть расслоение
множества переменных на подмножества независимых переменных выделяет в нем
подмножество мощности m. Тогда значение K определяется так:
2. В случае неравномерного разбиения множества переменных оценку
полученного выигрыша можно рассчитать следующим образом. Пусть расслоение
множества переменных на подмножества независимых переменных выделяет в нем
подмножество мощности m. Тогда значение K определяется так:
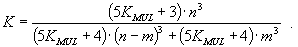 |
15 |
Разрешим неравенство
 |
16 |
Эквивалентные преобразования (16) с учетом (15) приводят к условию
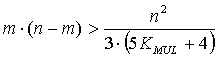 |
17 |
Учитывая, что нашей задачей является отыскание наименьшего m, превращающего неравенство (17) в истинное, будем считать, что
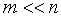 |
18 |
Тогда возможно принять
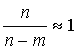 |
19 |
и неравенство (17) приобретает окончательный вид
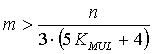 |
20 |
Как уже было указано, минимальное значение KMUL с применением технологии кэширования составляет 2 раза, без кэширования на современных аппаратных платформах - 6 раз. С учетом этого коэффициент в знаменателе неравенства (20) для кэш-реализаций составляет 42 и более, для реализаций без кэширования - 100 и более раз, что на практике приводит к выигрышу в вычислительной трудоемкости выделения инвариантов подобия уже при отделении хотя бы одной независимой переменной.
Таким образом, при наличии в графе w(S) нескольких связных компонент использование методики обнаружений аномалий на основе инвариантов подобия практически оправдано. При этом вычислительные затраты на поиск и выделение связных компонент в алгоритме вычислительных процессов по сравнению с вычислительной трудоемкостью вывода инвариантов подобия не значительны.
Оценка быстродействия предлагаемой методики
Рассмотрим систему размерностей в терминах теории графов. В этом случае процесс проверки существования нетривиального или не имеющего нулей решения системы линейных уравнений сводится к проверкам подсистем, имеющих ранг, равный количеству содержащихся в них переменных. В фактор-множестве (G/α)/σ' подсистемам, обладающим подобными свойствами, соответствуют простые циклы (везде далее - циклы). Для проверки общей совместности системы, заданной матрицей s, достаточно проверить совместность некоторого подмножества подсистем, удовлетворяющего следующим критериям:
- объединение ребер, входящих в циклы, соответствующие элементам подмножества, должно равняться множеству ребер графа σ'(w(s)) (критерий покрытия всех уравнений системы);
- между любыми двумя циклами, соответствующими элементам подмножества, должен существовать путь, то есть цепь из других циклов, каждая соседняя пара циклов в которой имеет хотя бы одно общее ребро.
Возможность выбора подсистем множеством различных способов позволила разработать методику выбора подмножества подсистем, удовлетворяющего приведенным выше критериям и требующего минимального количества операций для проверки совместности. Припишем каждому циклу в графе σ'(w(s)) меру, пропорциональную вычислительной трудоемкости его проверки. Данный параметр можно принять прямо пропорциональным (например, равным) количеству ребер в цикле. Определим отображение Ψ: (G/α)/σ' -> H, где H - множество гиперграфов, следующим образом. Сопоставим каждому ребру графа-прообраза вершину в графе-образе, а каждому циклу - ребро (возможно степени выше 2).
Таким образом, в новом пространстве каждому уравнению системы ограничений соответствует вершина, а каждой потенциально несовместной подсистеме - ребро гиперграфа. Рассмотрим, например, граф gX , изображенный на рис. 1, соответствующий системе с 5 переменными, 6 связанными уравнениями и 3 простыми циклами. Условная стоимость проверки циклов A, B и C соответственно равна 3, 4 и 5 единицам.
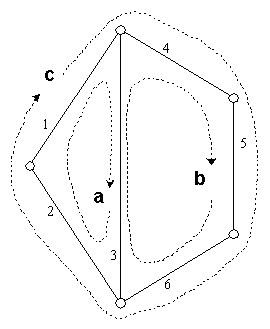
Рис. 1. Граф gX
Отображение Ψ переводит данный граф в гиперграф, изображенный на рис. 2.
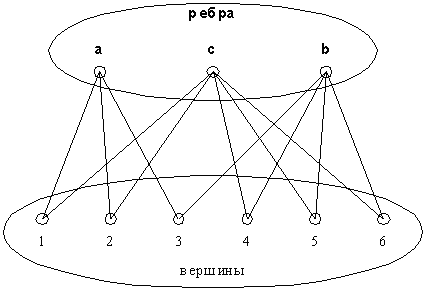
Рис. 2. Гиперграф Ψ(gX)
Тогда на множестве гиперграфов H необходимо построить минимальное остовное дерево, такой связной части графа, содержащей все его вершины, чтобы ее полная мера была минимальной. Эта задача близка к задаче коммивояжера, однако в рассматриваемом нами случае нет требований к поиску именно маршрута - решение может быть найдено в более широком подклассе графов - деревьях. Для решения поставленной задачи воспользуемся алгоритмом построения минимального остовного дерева для обыкновенных графов Р.С. Прим. Тогда получаем следующий алгоритм для пространства гиперграфов инвариантов подобия.
А л г о р и т м 1.
Шаг 1. Выбрать среди множества ребер графа ребро с минимальной мерой.
Шаг 2. До тех пор, пока часть содержит не все вершины, повторять пункт 3.
Шаг 3. Из множества ребер, инцидентных хотя бы одной вершине, входящей в уже построенную часть, и при этом инцидентных хотя бы одной вершине, не входящей в уже построенную часть, выбрать ребро с наименьшей мерой и добавить его к части.
Здесь для выбора оптимальной последовательности проверки взаимосвязанных циклов системы на первом шаге проверяется цикл наименьшей длины. Далее последовательно проверяются циклы, имеющие с уже проверенными хотя бы одно общее ребро, согласно возрастания их длин, до тех пор, пока не окажутся охваченными все ребра графа σ'(w(s)). Данный прием определяет план проверки потенциально несовместных подсистем, оптимальный относительно количества требуемых вычислительных операций.
Проверка работоспособности методики
Проверим вывод инвариантов подобия путем построения достаточного условия, например, на основании применения исчисления матрицы R по модулю простого числа. Для наличия в каждой строке матрицы C хотя бы одного ненулевого элемента достаточно, чтобы в каждой строке матрицы Cq , полученной из С путем вычисления остатка от деления соответствующего элемента на натуральное число q, существовал хотя бы один ненулевой элемент.
Действительно, пусть в i-й строке матрицы C все элементы равны нулю, тогда из определения матрицы Cq имеем
 |
21 |
Тогда достаточным условием вывода инвариантов подобия является требование, чтобы матрица C в системе уравнений размерности, построенной для него с учетом числовых констант и приведенной к виду, производя вычисления по модулю произвольного натурального числа q, не содержала нулевых строк.
Для корректного функционирования процесса необходимо, чтобы матрица C в системе уравнений размерности, приведенной к виду (4), не имела нулевых строк. Ранее было показано, что для выполнения этого условия достаточно, чтобы матрица Cq , полученная из матрицы C вычислением по модулю произвольного натурального числа q, не имела нулевых строк. Однако, в силу дистрибутивности операции вычисления остатка от деления на произвольно число q относительно операций сложения и умножения, применение исчисления по модулю q возможно уже на этапе приведения матрицы S к виду (4).
Данное условие является достаточным, но не необходимым. Действительно, при наличии в матрице Сq нулевых строк некоторые элементы в соответствующих строках в матрице С могут быть отличными от нуля, а именно - кратными q, а, следовательно, сам критерий может быть истинным. Приведенное условие преобразуется в необходимое, если поиск нулевых строк в матрице C производится для всех простых q. Более того, принимая во внимание диапазон исходных значений в матрице S и размерность матрицы S, возможно определить верхнюю границу списка простых чисел, достижение которой обеспечивает необходимость условия.
В общем случае трансформирование системы линейных уравнений по модулю простого числа имеет в три раза более высокую скорость исполнения. Это обусловлено отсутствием операций умножения рациональных чисел, каждая из которых содержит три операции умножения натуральных чисел (полагаем, что операции переноса и сложения имеют на порядок меньшую вычислительную трудоемкость по сравнению с операцией умножения). Исключение составляют исчисление по модулю 2 и по модулю 3.
Преобразование системы линейных уравнений по модулю 3 на множестве (-1, 0, +1) позволяет исключить из набора выполняемых операций умножение натуральных чисел. Все преобразования будут реализуемы с помощью сложения и арифметического отрицания. Это сокращает вычислительную трудоемкость проверки условия в несколько раз (в зависимости от параметров архитектуры ВС). Преобразование системы линейных уравнений по модулю 2 позволяет достичь еще большего быстродействия. Это достигается за счет возможности обрабатывать строки матрицы R как битовые последовательности, тем самым расходуя на сложение и перестановку строк по одной-двум командам микропроцессора. Перестановка столбцов при этом производится циклическими сдвигами двоичных значений.
Недостатками применения малых значений q при проверке необходимого условия является рост вероятности невыполнения условия при истинности значения критерия. Двумя величинами, критически влияющими на вероятность PFN в подобной ситуации, являются величина q и разность между количеством переменных и количеством условий, их связывающими (n-k). В первом приближении (без учета корреляции между значениями элементов матрицы R) данная зависимость описывается следующим выражением:
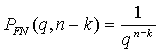 |
22 |
Кроме того, специфика предметной области обуславливает наличие в начале преобразований в матрице S в подавляющем числе значений (0, -1, +1), так как высокостепенные зависимости между переменными здесь достаточно редки. Это приводит на практике к неприемлемо высокому уровню PFN при (q = 2) даже в случае достаточно больших значений параметра (n-k). Поэтому предлагается:
- либо проверить достаточное условие для q=3, что увеличивает скорость вычислений в (3·KMUL) раз при выполнении условия и незначительно (в (1+(1/(3·KMUL))) раз) замедляет скорость вычислений при невыполнении условия;
- либо проверить условие для q=3 и для какого-либо простого q, большего трех, что увеличивает скорость вычислений примерно в 3 раза при выполнении условия и замедляет скорость вычислений в 1,33 раза при невыполнении условия.
(KMUL - коэффициент вычислительной трудоемкости операции целочисленного умножения по сравнению с операцией целочисленного сложения для данной аппаратной платформы).
Большее количество проверок с различными значениями q не приносит значимого увеличения средней скорости исчисления критерия. Выбор из предложенных вариантов производится на основе практических значений вероятности PFN и чаще всего обусловлен значением величины (n-k).
Выбор значения q, большего трех, для второго варианта проверки условия производится исходя из следующих соображений. Большие значения q более эффективны в связи с уменьшением вероятности PFN ложного невыполнения достаточного условия. Однако реализация линейных преобразований матрицы R по модулю q задействует предвычисления и хранение таблиц умножения и деления по модулю q, что требует определенных ресурсов вычислительной системы.
Варианты разработки систем обнаружения аномалий на основе инвариантов подобия
Как правило, датчики (или сенсоры) систем обнаружения вторжений размещаются в выделенных сегментах вычислительной системы (англ. термин - network-based IDS) или на рабочих станциях сегментов (англ. термин - host-based IDS). Поэтому выделим два возможных способа построения системы обнаружения аномалий на основе инвариантов подобия. В первом способе (рис. 3) датчики обнаружения аномалий размещаются в выделенном сегменте вычислительной системы. При этом основными функциями датчиков являются:
- перехват сетевого трафика между различными абонентами СПД;
- получение по совмещенному или выделенному каналу вектора (sK7 , sK6 , ... , sK1);
- проверка инварианта подобия семантически корректного вычислительныго процесса.
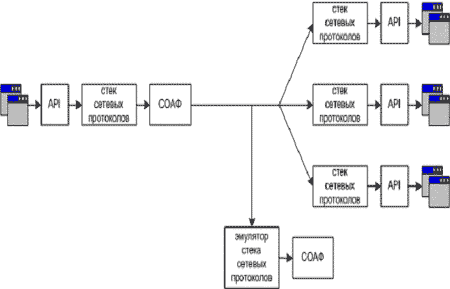
Рис. 3. Размещение датчиков СОАФ в широковещательных сегментах вычислительной системы
К достоинствам такой схемы системы обнаружения аномалий на основе инвариантов подобия относятся:
- защита инвариантов подобия вычислительных процессов от внутренних воздействий;
- коррекция аномалий вычислительных процессов в реальном масштабе времени в контролируемром сегменте СПД;
- минимальные затраты на организацию выделенного канала передачи инвариантов подобия.
Вместе с тем необходимо отметить следующие тенденции развития современных и перспективных вычислительных системах, которые существенно влияют на технологию обнаружения аномалий:
- сокращение доли широковещательных сегментов в современных сетях передачи данных;
- распространение систем шифрования трафика на сетевом уровне, в том числе разработка и пробное внедрение 6-й версии протокола сетевого уровня IP со встроенной поддержкой шифрования передаваемого трафика;
- значительное превышение скорости роста сетевого трафика над скоростью развития вычислительных ресурсов систем;
- возможность блокирования аномального сетевого трафика на этапе передачи его прикладному процессу;
- возиожность контроля реального функционирования стека сетевых протоколов.
Поэтому во втором способе (рис. 4) - датчики обнаружения аномалий размещаются на каждой рабочей станции внутри контролируемого сегмента вычислительной системы. Здесь основными функциями датчиков являются:
- получение по совмещенному (реже - выделенному) каналу вектора (sK7 , sK6 , ... , sK1);
- контроль локального стека сетевых протоколов;
- проверка истинности критерия.

Рис. 4. Размещение датчиков СОАФ на станциях-получателях
Теперь рассмотрим возможные варианты внесения избыточности в виде инвариантов подобия. Первый - на основе использования выделенной среды передачи информации (аналогичного и иного типа). Второй - путем использования совмещенной среды передачи информации.
Во втором варианте возможны две модификации, характеризующиеся либо выделением вектора (sK7 , sK6 , ... , sK1) в отдельное сообщение, либо интеграцией его с основным информационным сообщением.
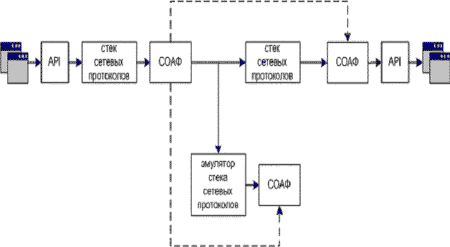
Рис. 5. Выделенный дополнительный информационный канал инвариантов подобия

Рис. 6. Совмещенный дополнительный информационный канал инвариантов подобия
Схема с выделенным информационным каналом для передачи вектора обладает следующими преимуществами:
- возможностью построить защищенный от прослушивания и модификации канал передачи информации об инвариантах;
- возможностью адаптивно управлять полосой пропускания, требуемой для передачи контрольной информации (в частности использовать физическую среду с меньшей пропускной способностью);
- минимальным интервалом задержки между получением датчиком информационного и контрольного пакетов.
Схему с совмещенным каналом передачи информационных и контрольных пакетов характеризуют следующие достоинства:
- минимальное изменение инфраструктуры и топологии сети на этапе внедрения системы;
- надежность доставки контрольного сообщения (особенно для варианта интеграции его в информационное сообщение) - невозможна ситуация, когда из-за пропадания контрольного сообщения станции-получателю придется проигнорировать корректный информационный пакет;
- меньшими затратами материальных ресурсов (особенно для схем с размещением датчика на станции-получателе).
Модификация данной схемы путем интегрирования контрольной информации в основное информационное сообщение обладает рядом дополнительных преимуществ. Среди них следует особо отметить:
- отсутствие задержки между приходом информационного и контрольного сообщений;
- возможность использования единой системы обеспечения целостности для информационной и контрольной частей сообщения.
Однако данная модификация применима не во всех случаях. Это связано с тем, что превышение ограничений на длину пакета, особенно на канальном и физическом уровнях, может быть некорректно обработано сетевым оборудованием. При этом даже при замене (или соответствующей корректировке) вычислительного процесса физического и канального уровня на приемной и передающей рабочих станциях возможен сбой со стороны промежуточного сетевого оборудования (модемов, концентраторов, коммутаторов).
Для протоколов сетевого уровня, поддерживающих дополнительную фрагментацию на произвольном сегменте маршрута пакета (к таким относится, например, протокол IP), данная проблема может быть решена на станции-отправителе K:
- либо установкой размера максимального фрагмента с учетом максимально возможного объема дополнительной информации об инвариантах;
- либо модификацией вычислительного процесса сетевого уровня с целью динамического определения длины текущего фрагмента.
Для протоколов сетевого уровня, не поддерживающих фрагментацию, данный метод неприменим. В любом случае, использование данной модификации возможно только в заранее проверенных системах передачи данных и при условии неизменности состава используемого сетевого оборудования.
Оценка вносимой избыточности инвариантов подобия
При реализации стеков сетевых протоколов в современных операционных системах принят де-факто принцип разбиения обработки передаваемых данных на уровни, соответствующие функциональной нагрузке. На каждом этапе обработки к результату предыдущего уровня добавляется служебная информация, и весь блок данных как неделимое целое передается на следующий этап обработки. Кроме этого при переходе между уровнями обработки возможен выбор протокола, который будет реализовывать функциональность конкретного уровня. Поэтому согласно стандарту "Взаимодействие Открытых Систем" (Open Systems Interconnection - OSI) международного Института Стандартизации ISO разделим контролируемые вычислительные процессы на семь уровней. При этом обозначим процессы, соответствующие уровням обработки данных как "pK7", "pK6", ... , "pK1" на передающей стороне, и "pL1", "pL2", ... , "pL7" согласно очередности их исполнения в системе. Тогда алгоритм обнаружения аномалий на основе инвариантов подобия принимает следующий вид.
А л г о р и т м .
- Параллельно исчислению реализаций уровней pK7 , pK6 , ... , pK1 вычислить на станции K (отправителе) элементы F(pK7) (sK7) , F(pK6) (sK6) , ... , F(pK1) (sK1).
- Проверить выполнение критерия

23 - Параллельно передаче на станцию L информационного сообщения с промежуточными результатами работы реализации передать вектор элементов X=(sK7 , sK6 , ... , sK1).
- Проверить выполнение критерия

24
Вновь вводимой по сравнению с известными подсистемами в данном алгоритме является подсистема передачи на станцию-получатель L вектора элементов X. Физическое представление данного элемента - это вектор из семи матриц системы ограничений размерности. Данная информация должна каким-либо образом быть закодирована и передана на приемную сторону с приемлемой задержкой относительно передачи основного пакета. При этом заметим, что матрицы sKi достаточно сильно разрежены в связи с характером взаимосвязей переменных в данной предметной области. Количество ненулевых элементов в строке не превышает 4 при общем количестве переменных от 5 до 30. В связи с этим предлагается следующая схема кодирования элементов вектора X на этапе передачи. На станцию-получатель L передается:
- количество задействованных в каждой системе sKi переменных;
- позиции переменных в заголовках сетевого пакета;
- количество строк в каждой из матриц sKi;
- значения элементов матриц sKi.
Количество задействованных в системе переменных передается в двоичном коде. Позиции переменных передаются двумя векторами VP и VL. Каждый элемент VPi вектора VP соответствует смещению в битах от начала заголовка соответствующего уровня до начала поля соответствующей переменной и кодируется двоичным кодом. Каждый элемент VLi вектора VL соответствует длине в битах поля соответствующей переменной в заголовке и кодируется двоичным кодом.
Количество строк в каждой матрице кодируется двоичным кодом. Для эффективного построчного кодирования матриц sKi предлагается следующая методика исходя из:
- сильной разреженности матриц;
- целочисленности коэффициентов в матрицах;
- группирования значений коэффициентов матриц вблизи числа 0.
Для каждой строки матрицы в пакет записываются векторы VN и VK. Каждый элемент вектора VN соответствует ненулевому коэффициенту текущей строки матрицы и хранит порядковый номер столбца с таким элементом в двоичном коде. Каждый элемент вектора VK хранит значение ненулевого коэффициента, соответствующего элементу вектора VN с тем же индексом, в каком-либо эффективном коде, например, коде Хаффмана.
Матрицы sK7 и sK6 (прикладного и представительского уровней модели OSI) передаются на станцию-получатель L однократно в момент установки соединения прикладного уровня. Для многих протоколов это соответствует установлению соединения сеансового уровня. Матрицы sK5 и sK4 вычисляются и передаются в начале каждого сообщения. Матрицы sK3 , sK2 , sK1 необходимо передавать для каждого пакета сообщения.
Произведем оценку объемов дополнительного трафика, необходимого к передаче на станцию-получатель L для реализации предлагаемого в данной работе метода. Доля трафика, порождаемого СОАФ, в общем сетевом потоке вычисляется как отношение его объема к сумме трех основных компонент трафика:
- собственно передаваемому информационному сообщению (M);
- служебной информации стека сетевых протоколов (TY(M));
- дополнительному трафику СОАФ (TV(M)).
Пусть E - максимальный размер пакета сетевого уровня, VAVG и VMAX - средний и максимальный объем закодированной матрицы sKi , YAVG и YMIN - средний и минимальный объем служебной информации сетевого протокола i-го уровня, KAAVG и KAMIN - среднее и минимальное количество сессий сеансового уровня, приходящихся на одно соединение прикладного уровня. Тогда средняя (PAVG) и верхняя (PMAX) оценки доли дополнительного трафика как функции от величины M - длины передаваемого сообщения - будут иметь следующий вид:
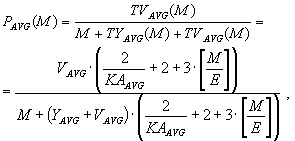 |
25 |
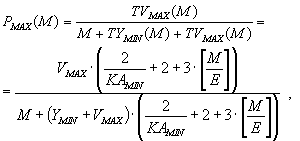 |
26 |
где TVAVG и TVMAX - среднее и максимальное значения дополнительного трафика как функции от M (квадратные скобки означают округление в большую сторону).
Для расчета величины V, исходя из описанной выше методики кодирования, справедлива следующая формула:
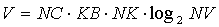 |
27 |
где NС - количество строк в матрице sKi, KB - средняя энтропия одного символа эффективного кода для значений коэффициентов матрицы sKi, NK - среднее количество ненулевых коэффициентов в строке матрицы, NV - количество переменных в системе ограничений размерности, описываемой матрицей sKi. Для расчета величины Y воспользуемся следующей формулой:
 |
28 |
где KP - доля переменных от общего числа, передаваемых в пакете, L - средняя длина одного поля (переменной) в пакете в битах.
Для определения VAVG, VMAX, YAVG, YMIN примем следующие значения данных коэффициентов (табл. 2.).
| Коэффициент | Значение | |
| при расчете VAVG | При расчете VMAX | |
| NC | 12 | 18 |
| KB | 2 | 2,5 |
| NK | 2,5 | 4 |
| NV | 12 | 24 |
| KP | 0,5 | 0,3 |
| L | 14 | 8 |
Исходя из этих данных, получаем значения, сведенные в таблицу 3.
Т а б л и ц а 3.
Оценки объема служебного трафика, добавляемого при обработке информации
| Величина | Значение | |
| при расчете VAVG | При расчете VMAX | |
| Трафик сетевогопротокола, Y | 84 (бит) = 11 (байт) | 29 (бит) = 4 (байт) |
| трафик СОАФ,V | 215 (бит) = 27 (байт) | 825 (бит) = 103 (байта) |
С учетом E = 1500 (байт), KAAVG = 3, KAMIN = 1 формулы (29) и (30) примут вид
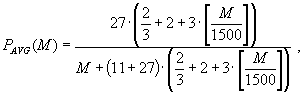 |
28 |
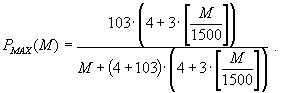 |
29 |
Графики зависимостей - на рис. 7 (шкала длины исходного сообщения - логарифмическая

Рис. 7. Зависимость средней (PAVG) и верхней (PMAX) оценок
доли дополнительного трафика от длины сообщения, в %
Асимптотический предел средней оценки доли дополнительного трафика при длине сообщения стремящейся к бесконечности равен
 |
30 |
асимптотический предел верхней оценки доли дополнительного трафика при тех же условиях равен
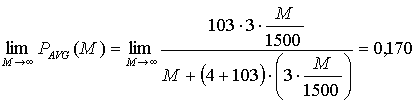 |
31 |
Таким образом, предложенная методика кодирования дополнительной информации обеспечивает приемлемый накладной прирост объема трафика при длинах сообщений, составляющих наибольшую долю в среднестатистическом сетевом трафике. Это подтверждает практическую применимость рассмотренной методики обнаружения аномалий на основе инвариантов подобия.
Защита инвариантов подобия
В случае передачи вектора (sK7 , sK6 , ... , sK1) по открытому каналу передачи данных необходимо обеспечить требуемую целостность сообщений. Без дополнительных средств защиты рассматриваемый метод обнаружения аномалий на основе инвариантов подобия уязвим на этапе передачи вектора X и возможны фальсификации сообщений, а также атаки методом повтора (от англ. reply attack).
Поэтому для защиты сообщений от фальсификации предлагается использовать алгоритмы электронно-цифровой подписи (ЭЦП), основанные на методах асимметричной криптографии, или алгоритмы имитозащиты, основанные на методах симметричной криптографии. В силу требования очень высокой скорости процессов вычисления и проверки тегов целостности более приемлемыми являются симметричные криптопреобразования.
Согласно методу обеспечения имитозащиты над открытым сообщением, которым в данном случае является вектор X, выполняются симметричные криптопреобразования. В процесс необратимым образом вовлекается блок секретной информации, известный только агенту-отправителю и датчику СОАФ, - ключ выработки имитовставки. Результат преобразований - блок фиксированной длины (имитовставка) добавляется к открытому сообщению. В качестве практической реализации для выработки имитовставки может быть использован алгоритм ГОСТ 28147-89 согласно спецификации либо любой алгоритм криптостойкой хеш-суммы (например, MD5 или SHA-1). Во втором варианте ключ выработки имитовставки добавляется конкатенацией к защищаемым данным (вектору X) перед выполнением хеширования.
Атака методом повтора заключается в изменении или замене злоумышленником пакета (в данном случае - позволяющего обнаружить несанкционированную активность в сети) на значение, ранее уже передававшееся в сети и приводящее к исчислению положительного значения критерия (28). При реализации данной атаки злоумышленнику не требуется производить подбор имитовставки или ключа ее генерации, его цель - сокрытие от системы своей несанкционированной активности. Возможность проведения подобных действий без атаки криптоалгоритма имитовставки делает задачу защиты от подобного класса атак актуальной для разрабатываемого способа. Для защиты от атаки методом повтора в защищаемое сообщение до выработки имитовставки добавляется:
- либо порядковый номер сообщения, уникальный для данной пары рабочих станций в пределах разумного периода времени;
- либо штамп времени высокой точности (с необходимостью высокоточной синхронизации машинных часов всех станций-абонентов СПД).
Возможна комбинация первого и второго метода с соответствующим уменьшением разрядности порядкового номера и загрублением точности системы синхронизации времени.
Параметры алгоритма обеспечения целостности дополнительного информационного потока рассчитываются из следующих соображений. Ключ выработки имитовставки является долгосрочным (функционирует в неизменном виде в течение достаточно долгого периода), в силу этого на него должны распространяться общие требования для симметричных криптоалгоритмов. В частности, считается стойкой на современном этапе развития электронно-вычислительной техники длина ключа в 256 бит.
Само содержимое имитовставки не является предметом какой-либо из известных криптоатак. Однако, генерируя хаотичным образом имитовставку для несанкционированного пакета, злоумышленник может случайно создать валидное ее значение. Данная атака является определяющей для выбора минимальной длины имитовставки: между двумя станциями за разумный временной интервал при использовании максимальной пропускной способности сети не должно быть возможным случайно сгенерировать валидную имитовставку.
Максимальное количество пакетов, которые можно создать на данном физическом носителе за определенный интервал времени, определяется формулой
 |
31 |
где BW - максимально возможная пропускная способность сети между злоумышленником и абонентом (в битах в секунду), Y - длина интервала времени (в годах), L - минимально необходимая для атаки длина пакета (в байтах). Для определения верхней границы NMAX примем значения BW = 109, Y = 20, L = 56. Тогда NMAX равняется (1,4·1015), что соответствует по порядку величины 250, и для достижения уровня надежности α = 0,999 длина имитовставки должна быть не менее
 |
33 |
С учетом требуемого аппаратной платформой округления данной величины до границы байта, получаем длину имитовставки в 8 байт. Данное дополнение является вполне приемлемым для предложенного способа. Так, например, при длине информационного сообщения в 16 кбайт, доля добавляемой информации об инвариантах будет составлять в среднем 5,43%, а доля векторов имитозащиты - 0,54% от общего трафика.
Таким образом, выбор конкретной схемы реализации СОАФ зависит от топологии сети и характеристик рабочих станций-абонентов. Задача обеспечения целостности дополнительного информационного потока является разрешимой на основе общеизвестных технологий и не несет критического увеличения требуемых ресурсов.
Заключение
Известно, что обнаружение аномалий вычислительных процессов в распределенных вычислительных системах на основе TCP/IP во многом определяет эффективность управления информационной безопасностью в отечественных структурах и организациях. Изучение специфики обнаружения аномалий указывает на необходимость построения некоторой метрики безопасности на основе эталонов или инвариантов семантически корректной (правильной с точки зрения безопасности) обработки данных. Метрики, которая позволяет измерять, учитывать, наблюдать, сравнивать и совершенствовать существующие корпоративные системы защиты информации. В настоящей статье обобщены, систематизированы и развиты практические результаты нового направления исследований в этой области на основе положений теории подобия. Важным моментом этого направления является возможность теоретически обнаруживать и парировать все виды внутренних и внешних воздействий (в том числе и ранее не известные), которые существенно влияют на функциональные свойства распределенных вычислительных систем на основе TCP/IP.