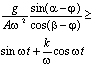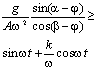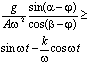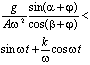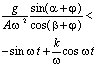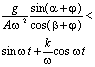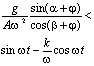УДК 621.86.067.2
В.Д.ИЛЬЧЕНКО, Т.И.ТУПОЛЬСКИХ
ИССЛЕДОВАНИЕ
ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА РАБОТЫ
ВИБРАЦИОННОГО ПИТАТЕЛЯ С БУНКЕРОМ
В
статье
рассмотрены теоретические и
экспериментальные исследования системы
бункер и питатель с вибрационным
приводом. Теоретические решения
истечения из боковой щели бункера
получены в представлении
мелкозернистого материала,
находящегося в бункере под воздействием
вибрации, как "псевдожидкости".
Перемещение слоя мелкозернистого
материала по дну лотка вибрационного
питателя, связанного с бункером единым
вибропобудителем, представлено в виде
движения частицы с сопротивлением,
пропорциональным вибрационной скорости.
Экспериментально найдены коэффициенты
истечения из прямоугольной боковой щели
бункера, определены коэффициент
сопротивления движению и
производительность питателя в
зависимости от параметров вибрации и
размеров частиц сыпучего материала.
Ключевые слова: истечение
из бункера, вибрационное перемещение,
вибрационный питатель, сыпучий материал
Введение. Обзор
существующих теоретических и
практических решений по истечению
сыпучих материалов из бункера и работ по
вибрационному перемещению слоя
мелкозернистого материала позволил
сделать следующие выводы.
Технологический процесс истечения
мелкозернистого материала из бункеров
достаточно подробно изучен для бункеров
большого объема при естественном
истечении, т.е. без вибрационного
воздействия на материал.
Технологический процесс истечения
мелкозернистого материала из малых
бункеров под воздействием вибрации
через боковую щель изучен недостаточно.
Рассмотренные
исследователями процессы истечения из
бункера мелкозернистого материала и
движение слоя такого материала не
связаны в единую цепь, что существенно
усложняет дальнейшие исследования и не
позволяет разработать стройную
методику инженерного расчета рабочих
органов дозаторов различных типов -
весовых и объемных. Все это затрудняет
дальнейшее совершенствование и
создание новых конструкций
вибрационных питателей.
Постановка задачи. Задачи
исследования технологического процесса
вибрационного питателя мелкозернистых
материалов с бункером состояли в
следующем:
разработать
математическую модель процесса подачи
сыпучего материала, подвергнутого
вибрационному воздействию, к
дозирующему устройству из боковой щели
бункера;
теоретически
исследовать процесс вибрационного
перемещения слоя сыпучего материала при
повышенной частоте вибрации и
обосновать режимы работы и параметры
вибрационного привода питателя;
получить
зависимость производительности
вибрационного питателя от параметров
вибрации и физико-механических свойств
сыпучего материала на основе теории
размерностей;
провести
экспериментальную проверку основных
теоретических положений;
на
основании полученных результатов
исследований разработать методику
расчета системы бункер – вибрационный
транспортер, обеспечивающей
совершенствование технологического
процесса дозирования сыпучих
материалов.
Теоретические решения. В
качестве рабочей гипотезы было принято,
что мелкозернистый материал в бункере
под воздействием вибрации представляет
собой "псевдожидкость". Такая
гипотеза позволяет применить
гидромеханические законы истечения
материала из бункера.
|
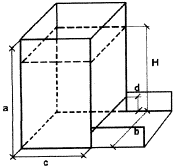
Рис.1.
Схема бункера с лотком |
Система
бункер - вибрационный лоток
представляет собой, обычно, бункер
прямоугольного сечения со щелью во всю
ширину бункера (рис.1), дном которого
является лоток, приводящийся в
колебательные движения тем или иным
способом. Наиболее часто лоток
соединен с бункером с помощью плоских
пружин или шарниров и приводится в
колебательные движения кривошипным
механизмом или электромагнитами.
Колебания лотка активизирует сыпучий
зернистый материал, поведение которого
можно уподобить поведению вязкой жидкости.
Поскольку в случае сыпучего материала
нарушаются некоторые допущения,
принятые при определении понятия
вязкости жидкости или газа, то многие
исследователи сыпучую среду из
мелкозернистого материала под воздействием
вибрации представляют как "псевдожидкость".
Исследуем динамику
истечения мелкозернистого материала из
бункера, используя аппарат
дифференциальных уравнений. Для большей
общности, предположим, что в бункер
постоянно подается мелкозернистый
материал с произвольной интенсивностью q м/с.
Допустим, что h
— напор в горизонтальном
сечении бункера, проходящем через
геометрический центр отверстия,
отвечающий установившемуся движению, т.е.
такой, что при этом напоре расход
сыпучего материала через отверстие в
точности равен притоку q.
Тогда
![]() .
.
Рассматривая элементарный
баланс сыпучего материала в бункере в течение
малого промежутка времени dt,
получаем дифференциальное уравнение,
связывающее высоту материала в бункере Н
и время истечения t,
которое после разделения переменных
имеет вид
![]() .
.
Частное решение
дифференциального уравнения истечения
мелкозернистого материала из бункера
под воздействием вибрации имеет вид
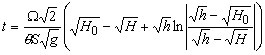 .
.
Напор
равновесия h физически
представляет собой точку подачи материала.
Если исходный напор H0 меньше (больше),
чем напор равновесия h,
то фактический расход из отверстия
будет увеличиваться (уменьшаться) с
течением времени. Соответственно, Н
будет замедленно возрастать (убывать),
приближаясь к равновесному значению h.
В частном случае, когда притока сыпучего
материала в бункер нет, т.е. h=0,
легко получить явное представление для
функции H(t):
 .
.
Перемещение
слоя мелкодисперсного материала
исследуем при допущениях, что дно
вибрирующего лотка представляет собой
плоскость, совершающую гармонические
колебания. Направление колебаний
составляет угол b
к
плоскости. Сама плоскость наклонена под
углом a
к горизонту. Движение слоя
мелкодисперсного материала под
воздействием вибрации отличается от
движения отдельной частицы. Этим
отличиям способствует форма и размер
частиц, образующих слой, толщина слоя,
влажность частиц, их упругие свойства,
воздухопроницаемость слоя, характер
взаимодействия материала, из которого
состоит слой, и материала поверхности,
внутреннее трение и силы взаимодействия
между частицами. Эти свойства слоя
начнут проявлять себя при его движении,
как только его толщина станет более, чем
размер одной частицы.
Все
факторы, влияющие на движение слоя, были
представлены силой Ф сопротивления движению,
пропорциональной вибрационной скорости,
![]() .
.
В
таком случае дифференциальные
уравнения движения слоя мелкодисперсных
частиц по колеблющейся поверхности
лотка питателя примут вид

Направление
действия силы трения F
зависит от направления относительной
скорости движения слоя, и это приводит к
появлению различных видов перемещения
слоя: движение вместе с плоскостью (остановку),
движение "по" и "против"
направления оси абсцисс и движение вне
плоскости.
Для
получения численных значений
перемещения и скорости движения слоя
интегрировать дифференциальные
уравнения движения с учетом переменного
направлением действия сил трения F
и сопротивления Ф
необходимо по моментам перехода от
одного вида движения к другому.
Уравнение
движения слоя мелкозернистых
материалов по дну вибрационного после
интегрирования лотка имеет вид
![]() .
.
В
табл.1 представлены условия движения
слоя мелкозернистого материала. Правые
части условий зависят от угла колебаний wt и
коэффициента k, а
левые части представляют
собой постоянные величины, определяемые
конструктивными параметрами
вибрационного лотка и коэффициента
трения материала о поверхность лотка.
Таблица
1
Условия
движения слоя мелкозернистого
материала
|
Результат
выполнения условия |
wt = |
|||
|
0…p/2 |
p/2…p |
p…3/2p |
3/2p…2p |
|
|
Движение вниз
или остановка |
|
|
|
|
|
Движение вверх |
|
|
|
|
Теоретические
исследования движения слоя
мелкодисперсного материала вне дна
лотка питателя проведем при следующих
допущениях. Слой движется как неупругая
частица, в момент отрыва имеет скорость,
равную вибрационной скорости плоскости,
влияние толщины слоя выражается силой
сопротивления, пропорциональной
скорости движения слоя вне плоскости,
при соприкосновении слоя с плоскостью
после окончания полета происходит неупругий
удар, и слой мгновенно приобретает
скорость плоскости.
Дифференциальные
уравнения движения слоя описанного
режима имеют
вид:
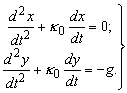
Для
выбранных начальных условий решения
дифференциальных уравнений движения
имеют вид
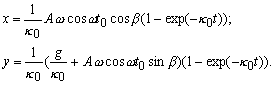 (1)
(1)
Начало
выполнения условий движения слоя вне
дна лотка
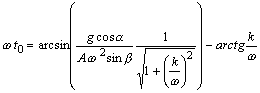 .
.
Конец
выполнения условий движения слоя вне
дна лотка
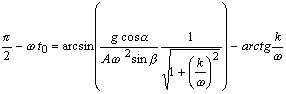 .
.
При
вертикальном ускорении 18,2 м/с2,
частоте колебаний w=628,3с-1, если
коэффициент сопротивления k больше 2000 с-1,
угол отрыва достигает максимального
значению p/2,
т.е. отделения слоя от дна лотка не
происходит.
Выражение, определяющее
момент wtп встречи
слоя с плоскостью, имеющее вид
![]() ,
,
может быть решено численно
или графически для конкретных значений
амплитуды, частоты вибраций и
коэффициента сопротивления
k0 при
свободном движении.
Для случая, когда слой встречается с
плоскостью в момент выполнения условий
отрыва
![]() , получим оценку вибрационного
ускорения, реализующего указанный режим:
, получим оценку вибрационного
ускорения, реализующего указанный режим:
![]() .
.
Получить численное решение
уравнения (1) перемещения для выбранного
режима колебаний и физико-механических
свойств мелкозернистых частиц сложно
ввиду нелинейности и разрывности
уравнений движения. На основе
экспертных оценок определено, что
производительность вибрационного лотка
питателя зависит от следующих
параметров, расположенных в порядке
приоритета: вибрационной скорости Аw,
вибрационного ускорения
Аw2
, угла направления колебаний
b,
угла наклона дна лотка к горизонту a,
поперечного сечения потока сыпучего
материала на лотке S,
угла трения f сыпучего
материала о материал лотка.
Предварительные
исследования поведения слоя под
воздействием вибрации показали, что на
производительность вибрационного лотка
влияет проекция вибрационной скорости Awcosb на
поверхность дна питателя.
В то же время на сыпучесть слоя и,
как следствие, на производительность
лотка оказывает значительное влияние
проекция вибрационного ускорения Aw2sinb
на нормаль к поверхности дна питателя. Однако
проекция гравитационного ускорения gcosa
на ту же нормаль уменьшает сыпучесть
слоя.
Влияние
сил трения слоя мелкодисперсных частиц
о поверхность дна питателя на
производительность можно выразить
следующим комплексом:
![]() .
.
Функциональную зависимость
производительности q вибрационного лотка представим в таком
виде:
![]() .
.
Наилучшим
образом выбранную функциональную
зависимость можно выразить
потенциальной зависимостью
между параметрами
![]()
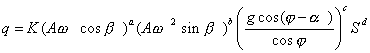 .
.
Количество критериев в
искомом критериальном уравнении можно
определить при помощи теоремы Бэкингема,
так называемой p-теоремы,
согласно
которой общая функциональная
зависимость, связывающая между собой n переменных
величин, при составлении которых
использованы p
первичных
единиц измерения, может быть
представлена в виде критериальной
зависимости между (n-p)
критериями подобия или безразмерными
комплексами,
составленными из величин, входящих в
общую функциональную зависимость. В
нашем случае n
= 5, p = 2, (n -
p) = 3.
Составив функциональную
зависимость в виде степенной
функции, заменим величины формулами
размерностей этих величин и,
сгруппировав величины
по показателям степеней, после
преобразований получим критериальное
уравнение в виде
 .
(2)
.
(2)
В уравнении (2)
мы образовали безразмерные
комплексы, которые позволяют корректно
провести эксперименты для вычисления
параметров K, c,
d.
Для определения
параметров K, c,
d критериальное уравнение (2)
необходимо представить в
логарифмическом виде
![]() ,
,
где
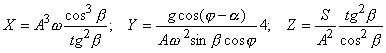 .
.
Экспериментальная
установка.
Экспериментальная установка состояла
из вибрационного питателя с бункером и
системы управления экспериментом. Лоток
питателя присоединялся к бункеру через
плоскую пружину, которая могла
устанавливаться под углами 600 , 700
и 800 к плоскости дна лотка, при этом
угол направления колебаний b
составлял 30°, 20° и 10°. Бункер соединялся
с рамой гибким звеном, тем самым
создавалась система из двух масс:
бункера и вибрационного лотка,
присоединенного к бункеру через
плоскую пружину.
Вибрационное перемещение
лотка и бункера осуществлялось с
помощью электромагнитного вибратора.
Частоты возбуждения лежали в диапазоне
20-400 Гц. Более высокая частота вызывает
большие потери в сердечнике
электромагнита из электротехнической
стали, снижая энергию для возбуждения
колебаний в системе.
Мощность,
подаваемая на вибратор, могла
изменяться, тем самым изменялась
амплитуда колебаний. Угол наклона лотка
к горизонту изменялся в пределах ± 5°. Толщина
слоя на лотке регулировалась от 0,005 до
0,015 м. Количественную информацию о
процессе получали измерением
производительности бункера или лотка с
бункером. В качестве мелкозернистых
материалов использовали: крупа
гороховая, пшено, мука, соль поваренная
помола №1.
Частота
колебаний задавалась экспериментатором
и замерялась частотомером марки Ч3-38.
Параметры вибрации: амплитуда,
вибрационная скорость и вибрационное
ускорение замерялись цифровым
виброметром марки ИВ1.
Результаты
эксперимента и их обсуждение.
Коэффициент истечения q
вычислялся по уравнению
![]() .
.
Эксперименты
показали, что коэффициент истечения q
при различных частотах колебаний не
зависит от наполнения Н бункера. Из этого следует, что
принятые допущения о характере течения
мелкозернистого материала,
находящегося под воздействием вибрации,
как "псевдожидкости" верны.
Экспериментально
выявлено, коэффициент истечения q зависит
от вертикальной составляющей
вибрационного ускорения и может быть
найден из зависимости
![]() .
.
На
коэффициент истечения q оказывает
влияние размер частицы.
Экспериментальные измерения выявила
линейную зависимость между
коэффициентом истечения и размером
частиц de
![]() .
.
Коэффициент k
сопротивления движению не может быть
определен прямыми измерениями, поэтому
он вычислялся на основе экспериментов
сравнением экспериментальной скорости
перемещения с теоретически
рассчитанной скоростью для данных
условий эксперимента.
При расчете теоретической
скорости движения коэффициент
сопротивления движению k подбирался таким, чтобы
теоретическое значение скорости
совпадало с экспериментальным
значением. Результаты вычислений коэффициента
k в зависимости от толщины
слоя и амплитуды колебаний представлены
на рис.2.
Для
получения параметров критериального
уравнения (2) были проведены
эксперименты на вибрационном питателе.
После обработки результатов
экспериментов критериальное уравнение
представлено в виде, приближенном к
физическому описанию процесса перемещения
под воздействием вибрации для частиц с
эквивалентным диаметром de=2,75.10-3
м:
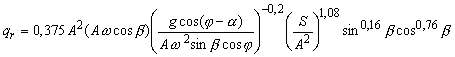 .
.
На
производительность лотка оказывает
влияние диаметр частицы. Для диаметров
частиц от 0,1 до 3 мм зависимость
производительности лотка от размеров
частиц хорошо описывается моделью
 .
.
|
Рис.2.
Изменение коэффициента
сопротивления движению k от толщины
слоя и амплитуды колебаний:
0,0000203 м, 0,0000304 м,
0,0000403 м, 0,0000507 м |
Интерес
представляет соотношение
производительностей бункера и лотка как
частей одного рабочего органа. Если
производительность лотка больше
производительности бункера, то это
приведет к неустойчивости движения продукта
по лотку и к сбою в дозировании
мелкозернистого материала.
В
табл.2 представлены производительности
бункера и лотка для одинаковых условий
вибрации и одного и того же
мелкозернистого материала. Производительности
бункера и лотка были рассчитаны для
условий: w= 628,3 с-1,
a= 0°, b=
20°, j = 0,34.
Мелкозернистый материал - гороховая
крупа с эквивалентным диаметром dэкв =2,75.10-3
м. Из таблицы следует,
что при различных вертикальных
ускорениях и минимальной высоте
материала в бункере всегда
производительность бункера оказывается
выше производительности лотка, что
создает условия для стабильной подачи,
например, при дозировании.
Таблица
2
Производительность лотка
питателя и бункера при одинаковых
условиях
|
Вертикальное
ускорение, м/с2 |
Поперечное
сечение слоя S, м2 |
|||||||
|
0,0006 |
0,0009 |
0,0012 |
0,0015 |
|||||
|
Бункер |
Лоток |
Бункер |
Лоток |
Бункер |
Лоток |
Бункер |
Лоток |
|
|
4,0 |
4,9E-06 |
2,5E-06 |
7,36E-06 |
3,93E-06 |
9,81E-06 |
5,36E-06 |
1,23E-05 |
6,82E-06 |
|
6,0 |
7,1E-06 |
3,9E-06 |
1,07E-05 |
5,99E-06 |
1,42E-05 |
8,17E-06 |
1,78E-05 |
1,04E-05 |
|
8,0 |
9,2E-06 |
5,2E-06 |
1,37E-05 |
8,08E-06 |
1,83E-05 |
1,1E-05 |
2,29E-05 |
1,4E-05 |
|
10,0 |
1,1E-05 |
6,6E-06 |
1,66E-05 |
1,02E-05 |
2,21E-05 |
1,39E-05 |
2,77E-05 |
1,77E-05 |
Выводы. Таким
образом, выбранная модель
мелкозернистого материала под воздействием
вибрации как "псевдожидкость"
оказалась плодотворной, что позволило
получить ценные для практики результаты.
Критериальное уравнение,
описывающее вибрационное перемещение
мелкозернистого материала по
вибрирующему лотку позволяет быстро и
просто выбрать режимы вибрации в
зависимости от конкретных условий
протекания технологического процесса
дозирования.
В системе бункер - вибрационный
питатель производительность лотка
всегда меньше производительности
бункера, что приводит к стабильности
подачи и устойчивости технологического
процесса дозирования.