ВЕСТНИК ДОННТУ

Одно из применений апостериорной обработки виброакустического сигнала в системах диагностики шахтных насосных установок   

Горелкин А.В.

Донецкий национальный технический университет, факультет КИТА, кафедра ЭТ

Постановка проблемы и ее актуальность.

.

Рисунок 1 – Структурная схема типичного измерительного канала диагностической аппаратуры

 Анализ известных решений.

Решить данную проблему возникающих искажений исследуемого сигнала можно решить двумя способами:

1 Применение цифровой фильтрации.  При таком решении структурная схема измерительного канала имеет вид:

Рисунок 2 - Структурная схема  измерительного канала диагностической аппаратуры с применением цифровой фильтрации

Как видно данная схема не лишена недостатков. От фильтра нижних частот стоящего перед АЦП не избавишся (т.к время преобразования АЦП конечно и исходя из теоремы Котельникова максимальную частоту в спектре измеренного сигнала, для того чтобы избежать искажений, придется ограничивать). ФЧХ такого фильтра зачастую также нелинейная. Цифровые фильтры будут  вносить задержку на один такт или, что еще хуже, на пол такта (в зависимости от того рекурсивный фильтр или нерекурсивный) это опять же нужно учитывать. И вообще цифровая фильтрация сложна в реализации, требует большого числа элементов с точным соблюдением номиналов.

2  Апостериорная обработка сигнала. Математический аппарат решения данной задачи отработан в области передачи изображений (причем очень давно). Там для решения этой задачи применялись "хитрые" технические решения, искажения сигнала изображения при прохождении среды компенсировались другой средой с обратными свойствами. Устранение искажений  сигналов в измерительных  электронных системах началось недавно и применительно к медицинским сигналам связано это с бурным развитием вычислительной техники и увеличением ее мощностей, т.к. устранение искажений происходит с применением аппарата преобразования Фурье, что требует больших вычислений. Суть сводится к следующему: пусть измерительный канал имеет передаточную характеристику H(w) (в частотной области) или соответствующую ей импульсную характеристику h(t)   (во временной области). При прохождении через измерительный канал сигнала x(t) преобразовывается в сигнал y(t)

или что тоже самое в частотной области

                      где    X(w) – преобразование Фурье от сигнала x(t);

                  Y(w) – преобразование Фурье от сигнала y(t).

Исходя из последнего выражения,  формально можно записать:

откуда обратным преобразованием Фурье найдем:

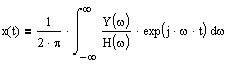
Однако применение последней формулы имеет ряд ограничений носящих чисто математический характер (интеграл должен быть сходящимся, функция H(w) отлична от 0 и т.д.) , который для технических сигналов не выполняется, единственной проблемой может служить лишь большая величина помехи которую нужно учитывать.

Основной материал и результаты исследования.

 Попытаемся промоделировать процесс устранения искажений вносимых в вибросигнал АФЧХ измерительного канала. В качестве сигнала возьмем сигнал вибрации подшипника с раковиной на наружном кольце. Вид такого сигнала представлен на рис.3.

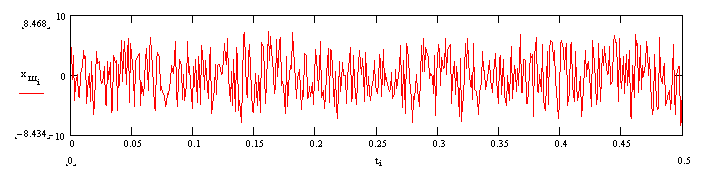
Рисунок 3 - Сигнал вибрации подшипника с раковиной на наружном кольце

Спектр данного сигнала имеет вид:

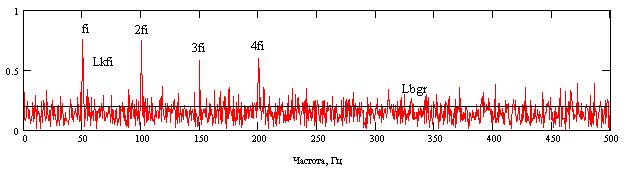
Рисунок 4 -  Спектр сигнала вибрации подшипника с раковиной на наружном кольце

При отсутствии дефектов спектр огибающей имеет только фоновые (случайные) составляющие с близкими по величине уровнями, так как в выбираемой третьоктавной полосе сигнал вибрации является стационарным случайным процессом. Дефект поверхности трения приводит к модуляции вибрации определенной частотой fi, и в спектре появляется ряд гармонических составляющих на частотах kfi, причем k может иметь как одно значение, например k=1, так и группу k=1,2,3,... Вид дефекта определяется частотой модуляции fi и числом k обнаруженных гармонических составляющих. Величина дефекта определяется разностью уровней DL максимальной из гармоник Lkfi и фона Lф.

Пропустим данный сигнал через измерительный канал, представленный  фильтром нижних частот (фильтр Баттерворта 2-го порядка)  подавляющим шумовые составляющие, конечно реальные схемы намного сложнее, но для демонстрации принципов этого хватит. Это сделаем  перемножив передаточную характеристику фильтра со спектром сигнала. Выражение передаточной функции фильтра имеет вид:

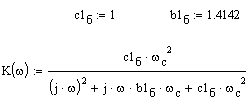
где частота среза w_с=440p рад/с (220 Гц).

Полученный спектр с помощью обратного преобразования Фурье переведем во временную область получим отфильтрованный сигнал, также в полученном спектре устраним фазовые искажения  разделив произведение спектра измеряемого сигнала и АФЧХ фильтра на аргумент передаточной функции К(w) и сравним полученные сигналы.

Рисунок 5 – Сравнение отфильтрованных сигналов и исходного

Как видно из рисунка сигнал с устранением искажений вызванных ФЧХ измерительного канала куда более соответствует исходному сигналу чем сигнал без устранения искажений.

Выводы

В ходе работы были предложена методика повышения достоверного анализа неисправностей шахтных насосных установок.

Литература

1.   2 Ярославский Л.П. Цифровая обработка сигналов в оптике и голографии.–М.: Радио и связь, 1987 г.

2.   Василенко Г.И. Теория восстановления сигналов: О редукции к идеальному прибору в физике и технике.–М.: Сов. радио, 1979 г.

3.   Гутников В.С. Фильтрация измерительных сигналов.–Л.: Энергоатомиздат. Ленингр. отд-ние, 1990 г.

4  Хемминг Р.В. Цифровые фильтры/ Под ред. О. А. Потапова..–М.: Недра, 1987 г