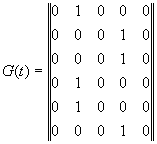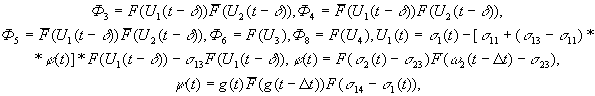Иванова О. Ю., магистрантка гр. АТ-99,
Рафиков Г. Ш., к.т.н., доц. каф. АТ.
Материал ,будет опубликован в сборнике научных трудов факультета КИТА

УДК 621.446

ИССЛЕДОВАНИЕ МОДУЛЯ ГЕНЕРАТОРОВ ШАГОВЫХ ЦИКЛОВ ПРИ РАЗЛИЧНЫХ ТИПАХ ОПОРНОЙ ПОВЕРХНОСТИ
Рафиков Г.Ш., Иванова О.Ю.
Донецкий национальный университет, КИТА, АТ-99

Разработка внедорожного транспортного средства, обладающего более высокой грунтовой проходимостью, определяется необходимостью перемещения объектов большого веса и габаритов по грунтам с низкой несущей способностью. Использование традиционных транспортных машин для размещения на них объектов весом во много десятков или сотен тонн в таких условиях крайне затруднено, так как на мягком грунте колесо, погружаясь в почву, оставляет глубокую колею, что в сочетании со значительной работой по деформации грунта приводит к резкому увеличению сопротивления движению. Шагающий аппарат, проваливаясь в грунт, не ухудшает своих тяговых характеристик, и не оставляет сплошной колеи, что важно как для выполнения транспортной функции, так и для защиты окружающей среды, ее почвенного покрова.

Шагающая машина должна использовать заложенные в принципе шагания возможности развязки движения корпуса машины от дороги. За счет изменения движения стоп относительно корпуса шагающая машина может обеспечить комфортабельное (равномерное и прямолинейное) движение корпуса машины при перемещении по поверхности с неровностями, достигающими величины дорожного просвета машины. Необходимость изменения траектории движения стопы относительно корпуса возникает и при движении по слабым грунтам для компенсации деформации грунта, величина которой различна для разных ног. Для обеспечения высокой проходимости шагающей машины при преодолении крупных препятствий необходимо использовать возможности изменения дорожного просвета, бокового выноса ног, длины шага, наклона корпуса машины относительно опорной поверхности. Маневренность связана с заложенными в шагающий аппарат возможностями движения вперед, назад, вбок и вообще с произвольным углом между направлением движения и продольной осью машины. Шагающая машина может совершать повороты и развороты на месте. Работа ног при повороте принципиально не отличается от работы ног при движении по прямой.

При создании шагающего аппарата, представленного на рис. 1, важнейшей является задача построения его системы управления, одна из функций которой состоит в поддержании заданной походки аппарата и осуществлении перехода с одной походки на другую в процессе движения, которая реализуется в блоке формирования походки.

Сложность программной реализации состоит в том, что уравнения которые описывают работу генератора представляют собой дифференциальные уравнения зависящие от логических функций. По этим уравнениям получаем траектории шагового цикла, которые позволяют отслеживать реализацию различных походок, их смену. По этой траектории можно судить о неровности поверхности.

Целью данной работы является исследование генераторов шаговых циклов, т.е. получение траекторий шагового цикла при различных типах опорной поверхности.

На рисунке 1 изображен шестиногий шагающий аппарат. Система координат Oxyz жестко связана с корпусом аппарата. Ось Ox направлена вперед по движению аппарата. Положение корпуса относительно осей абсолютной системы координат O₁ξηζ определяется координатами точки O корпуса аппарата и тремя углами (тангаж, крен, рысканье). Каждая нога аппарата состоит из трех звеньев, которые будем называть соответственно платформой, бедром, голенью. Звенья ноги лежат в одной плоскости, которая параллельна оси Oz. Положение ноги относительно корпуса определяется углами: α₁ – угол в шарнире платформы, α₂ – угол в шарнире бедра, α₃ – угол в коленном шарнире [1].


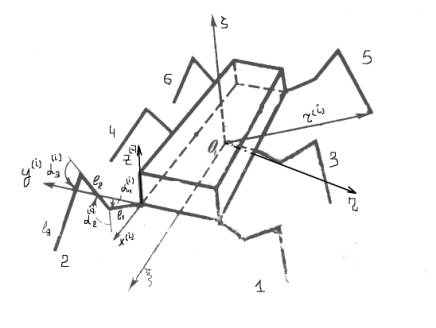
Рисунок 1 - Шестиногий шагающий аппарат

Походки аппарата подразделяются на группы: маршевые (использующиеся при ходьбе по пересеченной местности) и особопроходимые (при пересечении различных препятствий) [2].

К маршевым относятся, например, «трешка»


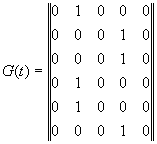
Шесть идентичных генераторов шаговых циклов формируют прообразы траекторий движения концов ног аппарата на плоскости вспомогательных декартовых координат 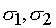,как решение системы дифференциальных уравнений вида
,
,
,
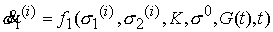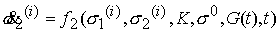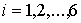где К — вектор управлений, 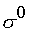— вектор параметров.

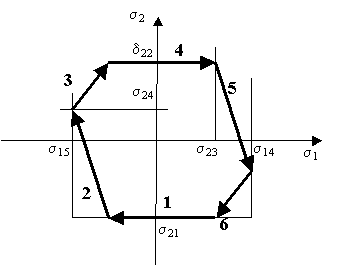
На рисунке-2 показаны плоскость ,
1 — фаза опоры; 2 — фаза переноса,участок отрыва; 3—фаза переноса, участок подъема; 4—фаза переноса; 5—фаза переноса, участок опускания; 6—фаза опоры, участок наступания [3].
Рисунок-2 Характерный вид траектории шагового цикла

Работа генератора шагового цикла определяется следующими уравнениями:




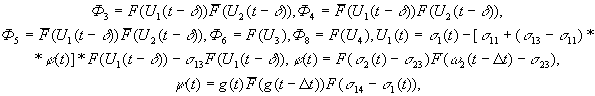
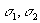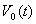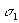
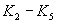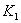где -координаты изображающей точки; - скорость движения изображающей точки в фазе опоры вдоль оси параметры генератора, определяющие углы наклона отдельных участков траектории изображающей точки; - параметр, определяющий скорость движения изображающей точки на фазе переноса; - время запаздывания срабатывания элементов сравнения; 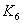- параметр, характеризующий декремент затухания обратных связей генератора; 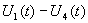- вспомогательные переменные; 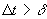- настраиваемый промежуток времени, в течение которого функци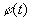и и 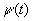отличны от нуля; 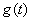- выход блока последовательности движения конечностей.
Параметры генератора удовлетворяют следующим условиям:
,

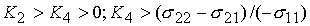
При моделировании генераторов шагов циклов были получены следующие результаты. Для жестких опорных поверхностей траектория шагового цикла в фазе переноса в участке отрыва и в участке опускания занимает мало времени по отношению с другими фазами [4]. Это объясняется тем, что поверхность прочная и не требует особой осторожности и анализа поверхности. На рисунке 3 показана типичная траектория шагового цикла для жесткой поверхности.

Рисунок 3 - Траектория шагового цикла 1
Частный случай жесткой опорной поверхности прочная ровная местность. Для этого случая на рисунке 4 приведена траектория шагового цикла. Фазы отрыва и наступания, подъема и опускания равны соответственно.

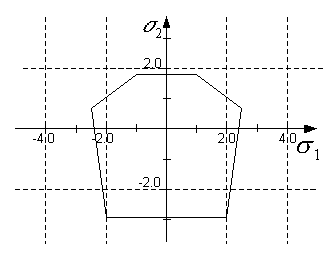
Рисунок 4 - Траектория шагового цикла 2 Для деформируемых опорных поверхностей фаза переноса в участке отрыва и в участке наступания больше по сравнению со случаем с жесткой опорной поверхностью. Аппарату необходимо больше времени для анализа поверхности, так как он более сложен.
Фазы подъема и опускания занимают больше времени, по сравнению с жесткой поверхностью, так как появляются выступы и уступы. Скорость аппарата снижается, следовательно фазы опоры и переноса почти равны.
На рисунке 5 показана типичная траектория шагового цикла для деформируемых опорных поверхностей.

Рисунок 5- Траектория шагового цикла 3.

Для слабых грунтовых образований скорость движения аппарата сильно снижается. Это связано с тем, что существенно увеличивается фаза переноса в участке отрыва и в участке опускания, фаза переноса уменьшается.
На рисунке 6 показана типичная траектория шагового цикла для слабых грунтовых образований.br>
Рисунок 6 – Траектория шагового цикла 4
Для неровных местностей фазы переноса в участках подъема и опускания изменяются в зависимости от того, какой выступ или уступ переходит аппарат.
В данной работе получена математическая модель генератора.
Записана вектор-функция для походки «трешка».
Графически и математически представлены фазы опоры, отрыва, подъема, переноса, опускания, наступания.
Даны ограничения параметров генератора шаговых циклов.
Приведены экспериментальные траектории шаговых циклов, которые дают всю информацию о поверхности, по которой перемещается аппарат, его скорости передвижения.
СПИСОК ССЫЛОК
1. Охоцимский Д. Е., Платонов А. К., Математическое маделирование джинамики движения шагающего аппарата.: Препринт Ин-та прикл. математики АН СССР № 96. М., 1984. 28 с.
2. Голубев Ю. Ф. Моделирование динамики движения шагающего аппарата: Препринт Ин-та прикл. математики АН СССР № 128. М., 1979. 27 с.
3.Исследование робототехнических систем. Сб. научных статей.Отв. редакторы: И. М. Макаров, Д. Е. Охоцимский, Е.П. Попов A.М.: Наука, 1982. 246 с.