|
Иванова О. Ю., магистрантка гр. АТ-99,
Рафиков Г. Ш., к.т.н., доц. каф. АТ.
Материал опубликован в сборнике научных докладов на III Международной конференции "Автоматизация технологических объектов и процессов. Поиск молодых"
ИТЕРАЦИОННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ
РАСПРЕДЕЛЕНИЯ РЕАКЦИЙ ПО ОПОРНЫМ ТОЧКАМ ШЕСТИНОГОГО ШАГАЮЩЕГО АППАРАТА
«КАТАРИНА»
Иванова О. Ю., студентка; Рафиков Г. Ш. доц., к. т. н.
(Донецкий национальний технический
университет, г.Донецк, Украина)
Разработка
алгоритмов управления движением автоматического шестиногого шагающего аппарата
«Катарина» в сложных условиях бездорожья тесно связана с поиском методов
решения задачи распределения реакций по опорным точкам.
Целью
данной работы служит поиск решения распределения реакций по опорным точкам с
минимальными временными и вычислительными затратами.
В данной работе предложен приблеженный метод решения задачи распределения
реакций, который был смоделирован с помощью встроенного в AutoCAD 2000 языка VBA
[1]. Использование многогранных углов вместо
конусов трения позволяет приблизится к точному распределению реакций путем
увеличения числа граней многогранника, апроксимирующего конус трения. Но этот
метод повышения точности сопряжен с существенными затратами счета и памяти ЭВМ.
В данной работе предлагается итерационный метод, позволяющий получать
достаточно точное решение задачи распределения реакций по точкам опоры
шагающего аппарата, ограничиваясь трехгранником в качестве апроксиматора конуса
трения [2].
Для реализации заданного движения необходимо, чтобы реакции в опорных точках
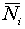 удовлетворяли системе уравнений кинетостатики
удовлетворяли системе уравнений кинетостатики
 ,
,
при имеющихся ограничениях
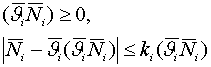 ,
,
где
 - реакция в i-той
опорной точке;
- реакция в i-той
опорной точке;
 - радиус-векторы, проведенные из центра масс аппарата в
опорные точки;
- радиус-векторы, проведенные из центра масс аппарата в
опорные точки;
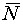 - сумма членов уравнения количества движения аппарата, не
содержащих опорных реакций;
- сумма членов уравнения количества движения аппарата, не
содержащих опорных реакций;
 -сумма членов уравнения кинетического момента аппарата, не
включающих реакций опоры;
-сумма членов уравнения кинетического момента аппарата, не
включающих реакций опоры;
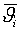 -единичные векторы внешней нормали к поверхности в точках опоры;
-единичные векторы внешней нормали к поверхности в точках опоры;
 -коэффициенты трения.
-коэффициенты трения.

Рисунок 1- шагающий аппарат «Катарина» с
указанными радиус-векторами и единичными векторами внешней нормали к
поверхности в точках опоры
Предполагаем,
что
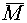

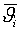
 известны.
Апроксимация
конусов трения правильным трехгранником происходит по следующей формуле
известны.
Апроксимация
конусов трения правильным трехгранником происходит по следующей формуле
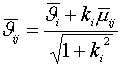 где
где

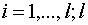 -число точек опоры;
-число точек опоры;  -число граней многогранника, апроксимирующего конус трения.
Апроксимация
i-той ноги
-число граней многогранника, апроксимирующего конус трения.
Апроксимация
i-той ноги
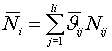 ,
,
где 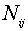 - неотрицательные числа.
После подстановки выражений получим:
- неотрицательные числа.
После подстановки выражений получим:
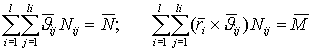 .
.
Cовокупность
неотрицательных чисел 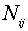 будет являться решением данной задачи. Используя
представление опорных реакций находим совокупность векторов
будет являться решением данной задачи. Используя
представление опорных реакций находим совокупность векторов
 ,
удовлетворяющих уравнениям , но, возможно принадлежащих не границам конусов
трения, а граням трехгранников.
Условие
принадлежности полученных реакций границам соответствующих конусов трения с
точностью до
,
удовлетворяющих уравнениям , но, возможно принадлежащих не границам конусов
трения, а граням трехгранников.
Условие
принадлежности полученных реакций границам соответствующих конусов трения с
точностью до 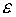 запишем в следующем
виде:
запишем в следующем
виде:
 .
.
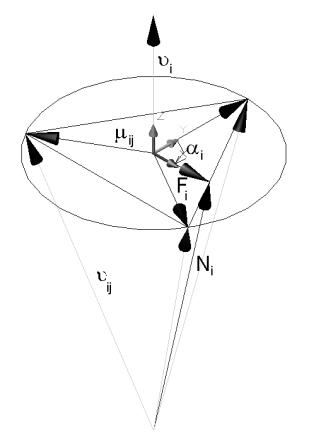
Рисунок 2- апроксимирующий трехгранник
Для
тех конусов трения, для которых реакция оказалась не на границе будем изменять
ориентацию соответсвующих трехгранников, путем поворота на угол  , вычисляемого следующим образом.
, вычисляемого следующим образом.
Введем
вектор  , тогда
, тогда
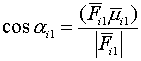 .
.
После
проверки условия для всех точек опоры и выполнения указанных выше действий
определяется ориентация всех трехгранников, необходимых для следующей
интеграции.
Таким
образом в работе была получена математическая модель метода.С
точностью до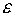 приведено условие
принадлежности полученных реакций границам соответствующих конусов трения.Дана
графическая интерпретация
рассматриваемого метода.Проведено
моделирование, целью которого был поиск распределения реакций аппарата при
использовании походки «галоп» в трехмерном пространстве по неровной местности.
приведено условие
принадлежности полученных реакций границам соответствующих конусов трения.Дана
графическая интерпретация
рассматриваемого метода.Проведено
моделирование, целью которого был поиск распределения реакций аппарата при
использовании походки «галоп» в трехмерном пространстве по неровной местности.
Перечень ссылок.
- Чепрушин А.Р. AutoCAD 2000 для пользователей. Днепропетровск-книга, 2001.
- Голубев Ф.Ю. Распределение реакций
при движении шагающего аппарата. Препринт ИПМ АН СССР, 1979, №123.
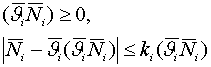 ,
,
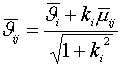
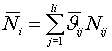 ,
, 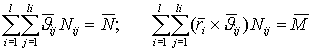 .
.
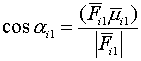 .
.