Введение

Предположим, что мы хотим изучить какой-то сигнал, например, временной ряд. Идея многомасштабного анализа (относящиеся сюда английские слова - multiscale и multiresolution), состоит в том, чтобы взглянуть на сигнал сначала под микроскопом, потом - через лупу, потом отойти на пару шагов, потом посмотреть совсем издалека.

Эта идея реализуется разными способами, но все они сводятся к последовательному огрублению той информации, которая дана изначально. Иногда действуют наоборот - сначала сильно огрубляют сигнал, смотрят на те особенности, которые еще сохранились, и начинают уточнять их положение.

Что это нам дает? Во-первых, мы можем выявлять локальные особенности сигнала и классифицировать их по интенсивности. Например, в обработке изображений широко распространена многомасштабная локализация резких границ (multiscale edge detection). Очень резкие перепады яркости заметны и на малых, и на больших масштабах. В некоторых задачах можно считать их наиболее информативной частью изображения, и вычислять с большой точностью, пренебрегая всем остальным. Вообще, подход последовательного уточнения чего-либо при переходе от крупного масштаба к мелкому возникает в самых разных областях обработки информации и прикладной математики. Хороший пример - многосеточные схемы в вычислительной физике.

Во-вторых, таким образом визуализируется динамика изменения сигнала вдоль "оси масштабов". Если резкие скачки во многих случаях можно заметить невооруженным глазом, то взаимодействие событий на мелких масштабах, перерастающее в крупномасштабные явления, увидеть очень сложно. Например, фрактальная структура каких-либо графиков или поверхностей бывает связана с (статистической) однородностью их строения на различных пространственных масштабах. Многомасштабный анализ помогает количественно охарактеризовать эту однородность. Скачки динамики по "масштабной переменной" могут нести не менее важную информацию, чем резкие изменения по времени или по пространству. Так, при анализе космических снимков земной поверхности выяснилось, что имеется несколько характерных масштабов, на которых фрактальные параметры меняются скачком. Также, и в экологии, и в экономике очень полезно выявлять ситуации, когда мелкомасштабная активность начинает влиять на крупномасштабную картину.

Часто в задачах обоих этих типов важнее найти не сами разномасштабные версии сигнала, а различия между ними, детали, которые исчезают при переходе от более тонкого масштаба к более грубому.

Вейвлет-анализ возник при обработке записей сейсмодатчиков в нефтеразведке и с самого начала был ориентирован как раз на локализацию разномасштабных деталей. Выросшую из этих идей технику теперь обычно называют непрерывным вейвлет-анализом. Ее основные приложения: локализация и классификация особых точек сигнала, вычисление его различных фрактальных характеристик, частотно-временной анализ нестационарных сигналов. Например, у таких сигналов, как музыка и речь, спектр радикально меняется во времени, а характер этих изменений - очень важная информация. Основным идеям непрерывного вейвлет-анализа и его приложений посвящен раздел 2.

Другая ветвь вейвлет-анализа - ортогональный вейвлет-анализ. О нем подробно рассказывается в разделе 3. Именно ортогональному вейвлет-анализу обязана своей популярностью вся эта тематика, с ним связана "вейвлет-революция" конца восьмидесятых годов. Главные применения - сжатие данных и подавление шумов.

Кроме этих двух важнейших частей вейвлет-анализа, имеется еще множество вариаций, которые очень кратко обрисованы в разделе 4. Там же приведен список важнейшей литературы, и электронные адреса, по которым можно найти много информации и полезные программы. А теперь перейдем, наконец, к изложению предмета статьи.

Непрерывный вейвлет-анализ.

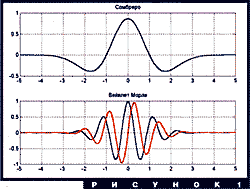
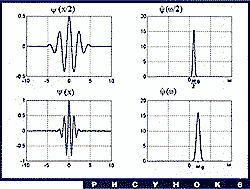
Главными действующими лицами этого раздела будут две функции, изображенные на рис. 1. Это - два самых, пожалуй, популярных вейвлета: "сомбреро" (Mexican hat) и вейвлет Морле (Morlet wavelet). График любого вейвлета выглядит примерно так же (заметим, что вейвлет Морле - комплекснозначный, на рисунке изображены его вещественная и мнимая части). Более точно, для того, чтобы функция могла называться вейвлетом, должны выполняться два условия.

1. Ее среднее значение (т.е. интеграл по всей прямой) равно нулю.
2. Функция быстро убывает при .

Теперь возьмем произвольный сигнал - некоторую функцию f(x) (переменную x будем называть временем), и произведем ее вейвлет-анализ при помощи вейвлета .

Результатом вейвлет-анализа этого сигнала будет функция Wf(x,a), которая зависит уже от двух переменных - от времени x и от масштаба a. Для каждой пары x и a (a>0) рецепт вычисления значения Wf(x,a) следующий:

1. Растянуть вейвлет в a раз по горизонтали и в 1/a раз по вертикали.

1. Сдвинуть его в точку x. Полученный вейвлет обозначим .

1. "Усреднить" значения сигнала в окрестности точки a при помощи .

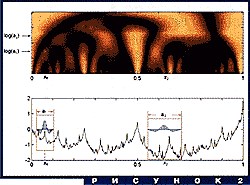
На рис. 2 показано, что надо сделать. В нижней части изображен график функции f(x), в верхней - условными цветами - распределение значений Wf(x,a) (по горизонтали - переменная x, по вертикали - ось a в логарифмическом масштабе, на которой маленькие масштабы расположены ниже больших. Самый маленький масштаб соответствует шагу сетки, на которой задана исходная функция). Синими столбиками изображены графики при разных значениях a и x. Выделенные участки графика исходной функции поточечно умножаются на значения оказавшихся над ними синих столбиков, потом все это суммируется. Абсолютная величина суммы определяет, какого цвета будет точка (x,a) на верхней картинке (на рисунке эти точки обведены красными кружочками). Это делается для всех пар (x,a).

Строгое определение выглядит так (это первая из двух обещанных формул).

(1)

На математическом языке можно сказать, что при фиксированном значении a Wf(x,a) есть свертка исходной функции с растянутым в a раз вейвлетом.

Посмотрим, какую информацию о сигнале можно получить из таких картинок. На рисунке 3 показано вейвлет-преобразование (с помощью "сомбреро") гладкой функции с единственной особенностью. Яркий конус точно указывает своей вершиной расположение этой особенности. Почему так происходит? На каждом уровне a = const стоит свертка f(x) с растянутой версией . В каждой точке это разность средних значений f по тем участкам, где положительна, и по тем, где она отрицательна. Так как среднее значение самой равно нулю, свертка напоминает "размазанную" производную данной функции. На малых масштабах размазывания почти нет, так как быстро убывает при удалении от x, и мы видим скачок вейвлет-преобразования (на картинке это более яркий цвет) вблизи самой особенности. На больших же масштабах растянутый вейвлет "задевает" особую точку, даже если он "приложен" к графику далеко от нее. Чем лучше вейвлет "сконцентрирован" во времени, тем точнее будет локализация особенностей.

А почему бы просто не вычислить производную или, скажем, вторые разности? В данном случае результат будет тот же - скачок в особой точке. Но давайте вернемся к рис. 2. Там тоже видны характерные яркие конусы, вырастающие из аналогичных особенностей функции. Но они соответствуют только самым сильным особенностям, имеющим большую амплитуду. Функция, которую мы изучаем, фрактальна, она не имеет производной нигде. Поэтому вторые разности дали бы совершенно хаотическую картину. Чтобы в ней разобраться, пришлось бы все сглаживать и перемасштабировать - что мы и делаем, проводя вейвлет-анализ! Мы пришли бы к аналогичной процедуре, но с плохим вейвлетом - плохим для другой важной задачи: выявления динамики локальных частот. Сейчас станет ясно, почему вейвлеты с рисунка 1 для этой задачи хороши.

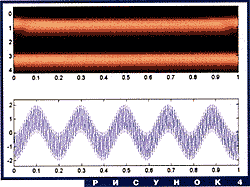
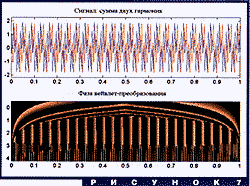
Обратимся к рис. 4. В верхней части изображено вейвлет-преобразование (на этот раз с помощью функции Морле, она лучше приспособлена к частотно-временному анализу) суммы двух чистых гармоник. В нижней - вещественная часть самой этой суммы. Четко выделяются две яркие горизонтальные полосы вида и . Частоты гармоник легко определить по этим значениям; они пропорциональны и .

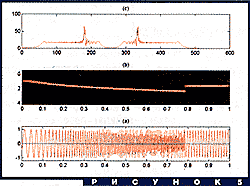
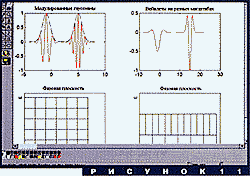
Возьмем более сложную функцию, частота которой сначала линейно меняется во времени, а потом скачком выходит на константу (рис. 5a). На рис 5b показано ее вейвлет-преобразование (с помощью вейвлета Морле). Мы видим наклонную яркую кривую, по которой можно определить начальную частоту, конечную частоту и характер изменения локальной частоты. В некоторый момент кривая превращается в горизонтальную прямую, которая соответствует чистой гармонике. Одного взгляда на эту картинку достаточно, чтобы полностью понять структуру сигнала. Для сравнения, на рис. 5c приведен спектр Фурье той же функции. Наглядность этого представления совершенно не сравнима с наглядностью рис. 5b. Характерные частоты можно усмотреть из пиков на спектре, но момент переключения никак не отражен.

Итак, вейвлет-преобразование дает существенную информацию о поведении сигнала в частотной области. Как это происходит, легко понять, взглянув на преобразование Фурье самого вейвлета Морле . Оно сконцентрировано вокруг некоторой выделенной частоты . Поэтому преобразование Фурье вейвлета, растянутого в a раз, будет сконцентрировано вокруг частоты . Это показано на рис. 6. Так как свертка функций эквивалентна их перемножению в частотной области, "строка" a = const на изображении вейвлет-преобразования показывает эволюцию изучаемой функции на частотах, близких к . Более подробно: умножение Фурье-спектра исходной функции на пик в точке в частотной области (т.е. на Фурье-образ растянутого вейвлета) вырезает из этой функции все то, что дает вклад в ее спектр на частотах, близких к . В результате получается развертка спектральной компоненты по времени.

Для того, чтобы такая схема давала осмысленные результаты, надо, чтобы Фурье-преобразование вейвлета было хорошо сконцентрировано вокруг . С другой стороны, для локализации особенностей необходима концентрация во временной области. В основном из этих соображений и выбирались анализирующие вейвлеты "сомбреро" и Морле. Вейвлет Морле был исторически первой функцией, получившей это название. Забавно, что, строго говоря, это не вейвлет - его среднее значение хотя и очень мало, но не равно нулю.

До сих пор мы обращали внимание только на амплитуду вейвлет-преобразования. В случае комплекснозначных вейвлетов много информации содержится в поведении фазы. Для примера посмотрим на рис. 7, где показана фаза вейвлет-преобразования суммы двух гармоник. Отчетливо видны два узора вертикальных полос, расположенные один над другим. Верхний узор, где полосы чередуются реже, соответствует низкочастотной гармонике.

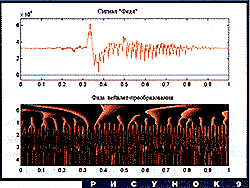
В более реалистической ситуации картинки становятся более запутанными. На рис. 8 показан модуль вейвлет-преобразования первых двух звуков слова "Федя". Четко видны горизонтальные полосы, соответствующие гармоникам звука "е", а также некоторые другие структуры, позволяющие в первом приближении сегментировать сигнал. На рис. 9 приведено распределение фазы вейвлет-преобразования того же сигнала. Здесь тоже можно легко заметить структуры такого же типа, как на рисунке 7. Более подробно о вейвлет-анализе речевых сигналов рассказывается в статье В.Спиридонова в этом номере журнала.

Непрерывный вейвлет-анализ дает возможность получить ценную информацию и о спектре Фурье. Так называемый вейвлет-спектр строится следующим образом: для каждого значения масштаба a вычисляется среднее значение модуля вейвлет-преобразования. Это дает усредненную величину обычного спектра в окрестности частоты . Усреднение тем грубее, чем выше частота. Тем самым производится разумное сглаживание спектра, позволяющее лучше уяснить его качественное поведение, выявить скрытые периодичности. В качестве примера приведем рис.10, где показаны вейвлет-спектр и обычный спектр части музыкального сигнала "Handel". Кстати, из этого рисунка видно важное свойство вейвлет-анализа - его способность различать частоты зависит не от их разности, а от отношения. Яркое применение этой техники (в сочетании с другими методами) к анализу многолетней динамики числа солнечных пятен представлено в статье П.Фрика и Д.Соколова.

Как известно, чем лучше функция сконцентрирована во времени, тем больше она размазана в частотной области. Это - принцип Гейзенберга. При перемасштабировании произведение временного и частотного диапазонов остается постоянным. Оно интерпретируется как площадь ячейки на "частотно-временной плоскости" (фазовой плоскости), информацию о которой можно получить с помощью данной функции. Идеальным инструментом анализа в этом смысле является гауссиан - замечательная во многих отношениях функция . Ее фурье-преобразование имеет точно такой же вид "колокола", как и она сама, а соответствующая ячейка фазовой плоскости - квадратик, имеющий минимальную возможную площадь (упражнение для внимательного читателя: почему эта функция не вейвлет?). В "довейвлетном" частотно-временном анализе эта функция играла очень большую роль. С ее помощью Деннис Габор (Dennis Gabor), получивший в 1971 году Нобелевскую премию по физике за изобретение им в 1947 году голографии, ввел свои знаменитые примитивы, которые он считал оптимальным средством представления сигналов. Это - модулированные гауссианы. Если модулировать их с разной частотой и сдвигать по времени, получаем преобразование Габора. Оно очень похоже на вейвлет-преобразование, надо только модуляцию заменить масштабированием, а вместо гауссиана взять вейвлет. Но есть и весьма существенная разница. Ее можно увидеть на рис. 11. Габор-примитивы покрывают фазовую плоскость одинаковыми квадратами; перемасштабированные вейвлеты - прямоугольниками постоянной площади, но разной формы. Благодаря этому вейвлеты хорошо локализуют низкочастотные "детали" сигнала в частотной области, а высокочастотные (всевозможные резкие скачки, пики, и т.п.) - в пространственной.

К рисунку 11 мы еще вернемся в следующем разделе, а этот раздел закончим кратким описанием очень полезного геометрического объекта, возникающего в вейвлет-анализе. Это - так называемый скелет максимумов (maxima skeleton). Он играет важнейшую роль в применениях вейвлетов к анализу фракталов и хаотической динамики, например, турбулентных течений. С этим связана довольно сложная математика, в которую мы вдаваться не будем, а ограничимся демонстрацией двух картинок.

Скелет максимумов - это, грубо говоря, множество точек на плоскости (x,a), в которых находятся локальные "пики" вейвлет-преобразования. Этих точек обычно очень много в области малых масштабов. Их появлением вейвлет-преобразование реагирует на любые негладкости сигнала. При росте масштаба мелкие негладкости исчезают, а вместе с ними и точки максимумов. Оставшиеся сливаются в довольно гладкие кривые, которые при дальнейшем росте масштаба тоже сливаются друг с другом. При этом они либо "аннигилируют", либо продолжают "расти" в область еще более крупных масштабов, и т. д. Типичная картина показана на рис. 12.

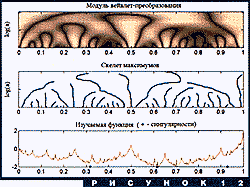
В определенном смысле, вся существенная информация о сигнале находится в значениях вейвлет-преобразования в точках скелета максимумов. Для широкого класса сигналов можно просто забыть все остальное. Важные для физиков фрактальные параметры турбулентных течений тоже можно вычислять при помощи значений преобразования только на скелете. Очень полезное свойство скелета - наглядное ранжирование особенностей сигнала по их "силе". У таких сигналов, как скорость жидкости в данной точке турбулентного течения, все точки особые, но все в разной степени. Сама их иерархия является важным физическим параметром, который можно оценить с помощью скелета максимумов. Например, можно предположить, что самые длинные линии растут из "самых особых" точек. Часто это предположение справедливо. Надо, впрочем, отметить, что такие вычисления - дело очень деликатное. Не вдаваясь в дальнейшие подробности, приведем последний в этом разделе пример.

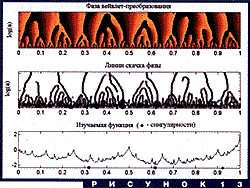
Фрактальная функция, изображенная на рис. 12, построена с помощью простой одномерной динамической системы. Имеется задача - узнать параметры этой системы по виду функции. Такая задача важна при фрактальном моделировании различных процессов (например, в экономике). В данном случае искомые параметры легко определить, если знать точки, где особенности сигнала, в определенном смысле, самые сильные. Сигнал модельный, поэтому эти точки заранее известны - это точки 0.31, 0.62 и 0.92. Визуально они совершенно незаметны на фоне резких пиков в других местах. На рис. 12 видно, что и линии максимумов тоже не помогают их найти - самые длинные линии растут из совсем других точек. Но если использовать комплексный вейвлет Морле, построить распределение фазы вейвлет-преобразования, и посмотреть на линии скачка фазы - резкие границы между темным и светлым, - мы увидим, что три из самых длинных линий вырастают почти точно из нужных нам точек. Все это показано на рис. 13. В более сложных случаях информация о максимумах модуля и скачках фазы используется совместно.

Мы бегло познакомились с некоторыми подходами к исследованию сигналов с помощью непрерывного вейвлет-анализа. Теперь обратимся к другому варианту реализации той же идеи многомасштабного представления сигналов.

Ортогональный вейвлет-анализ.

Картинки, построенные в предыдущем разделе, весьма информативны. На них видны свойства сигналов, совершенно не заметные на спектре Фурье. Но в этом нет ничего удивительного - ведь непрерывное вейвлет-преобразование требует во много раз больше вычислительной работы. Преобразование Фурье здесь вычисляется на каждом масштабе (для нахождения свертки с разномасштабными версиями вейвлета). В этой науке естественным образом возникают музыкальные термины - набор значений вейвлет-преобразования при фиксированном масштабе a называется голосом, диапазон масштабов (или, что то же самое, частот) от a до 2a - октавой. Классика подсказывает, что на каждую октаву надо взять по крайней мере 12 голосов (равномерно распределенных в логарифмической шкале). Так вот, если сигнал имеет скромную длину 4096 слов, то 8 октав займут 393216 (вообще говоря, комплексных) слов.

Избыточность такого представления огромна. Очень быстро стало ясно, что для точного восстановления исходного сигнала достаточно знать вейвлет-преобразование на некоторой довольно редкой решетке в плоскости (x,a). Следовательно, и вся информация о сигнале содержится в этом сравнительно небольшом наборе значений. Впрочем, преобразование Фурье тоже содержит всю информацию о сигнале; пафос непрерывного вейвлет-анализа не в наиболее экономном, а в наиболее информативном представлении частотно-временных и масштабно-временных свойств сигнала. Поэтому, возможно, ортогональные вейвлеты и возникли в другом контексте. Точнее, сразу и независимо в трех контекстах - в гармоническом анализе, квантовой механике и обработке изображений. Кратко остановимся на последнем.

В 1983 году Бэрт (P. Burt) и Адельсон (E. Adelson) написали небольшую статью о сжатии изображений при помощи пирамидального представления. В ней содержались основные идеи того, что позднее, после работ И. Мейера (Y. Meyer) и С. Малла (S. Mallat), получило название многомасштабный анализ (multiresolution analysis). Алгоритм Бэрта-Адельсона очень прост и изящен. Он строится для конечных дискретных сигналов, да и вообще в их работе никакой абстрактной математики, кроме слов "гауссиан" и "лапласиан", нет. Для одномерного случая конструкция такова (см. рис. 14).

Сигналу, заданному в дискретные моменты "времени", ставятся в соответствие две пирамиды - пирамида гауссианов (Gaussian pyramid), и пирамида лапласианов (Laplacian pyramid). Для этого выбирается очень простой сглаживающий фильтр (подавляющий высокие частоты), заданный всего пятью коэффициентами. Нулевой этаж пирамиды гауссианов - сам сигнал. Первый этаж - результат фильтрации нулевого этажа, прореженный путем выбрасывания каждого второго числа. В самом деле, половина частот подавлена (так подбирается фильтр), поэтому "интервал дискретизации" можно увеличить вдвое. Второй этаж строится таким же образом из первого, и т.д. Заметим, что на каждом шаге применяется один и тот же фильтр, но масштаб каждый раз удваивается.

Ставится задача сжатия данных, причем допускаются несущественные потери информации при "разжатии". Идея состоит в том, чтобы запомнить вместо сигнала его "детали" на каждом из масштабных уровней, а также самую грубую версию сигнала - последний этаж пирамиды гауссианов. В качестве деталей предлагается использовать разности между последовательными этажами пирамиды гауссианов. Но как их найти - ведь количество элементов в соседних этажах отличается вдвое? Рецепт такой: вставить нули между соседними значениями верхнего этажа (теперь их размеры совпадают!), профильтровать (с помощью все того же фильтра!), и то, что получится, вычесть из нижнего этажа. Двигаясь снизу вверх, получаем пирамиду лапласианов. В первом ее этаже столько же элементов, сколько в самом сигнале, во втором - вдвое меньше, и т.д.

Сигнал теперь можно забыть, по пирамиде лапласианов и верхнему этажу пирамиды гауссианов он восстанавливается точно.

Итак, вместо исходного сигнала мы получили другой сигнал, примерно вдвое большей длины. Где же сжатие? Оказывается, на нижних этажах пирамиды лапласианов стоят, как правило, очень маленькие величины. Дело в том, что в сигналах, для которых создавался этот метод, резкие скачки на малых масштабах встречаются редко. Большую часть этих величин можно заменить нулями - на восстановленном изображении это почти не скажется - а остальные записать более короткими словами, чем основной сигнал. Такой массив можно довольно сильно сжать обычными, обратимыми методами. А те этажи, где распределение данных такое же, как в исходном сигнале, занимают не так много места.

Итак, первая идея - многомасштабное представление строится применением одного и того же сглаживающего фильтра на последовательно удваивающихся масштабах. Вторая идея - сигнал компактно представляется в виде разностей между своими версиями разной подробности. Но в этой работе была еще одна замечательная идея - посмотреть, как выглядит фильтр, с помощью которого можно перейти с нулевого сразу на последний этаж пирамиды гауссианов.

Этот фильтр получается, если сначала подействовать исходным фильтром на единичный импульс, потом - на результат этого действия, и т.д. Оказывается, что (после перенормировки) возникает некая предельная функция, и ее форма связана с тем, хорошее или плохое сжатие получается при использовании данного фильтра. Бэрт и Адельсон построили несколько примеров таких предельных функций, и заметили, что результат, в среднем, тем лучше, чем более гладкой будет предельная функция.

Разобравшись в этом алгоритме, легко понять идеологию многомасштабного анализа Мейера-Малла. Она состоит в том, что "большое" пространство "всех возможных сигналов" надо исчерпать растянутыми и сжатыми копиями некоего "эталонного" пространства, порожденного ровно одним фиксированным сигналом , и его сдвигами. Это эталонное пространство, по определению, принимается за набор всех сигналов, которые можно представить с разрешением 1.

Простейший пример (рис. 15): - единичный "столбик" на интервале [0,1), его сдвиги - столбики на ...[-2,-1), [-1,0), [1,2),... . Эталонное пространство состоит из "лесенок", полученных домножением этих столбиков на произвольные числа.

Остальные пространства - перемасштабированные копии этого. Одно из них получается растяжением в два раза (в нашем примере - лесенки из столбиков ширины 2), другое - в четыре раза, еще одно - сжатием в два раза (столбики ширины 1/2), и так для всех положительных и отрицательных степеней двойки. Ясно, что измельчая ширину столбика, можно приблизить любой сигнал.

Далее, требуется, чтобы фиксированный сигнал , называемый скейлинг-функцией (scaling function, scalet), обладал двумя свойствами. Во-первых, его сдвиги вида ... должны быть друг другу ортогональны (то есть, в определенном смысле, никак между собой не коррелированы; в нашем примере это, очевидно, выполняется). Сигналы, представляемые с разрешением 2 можно представить и с разрешением 1 (столбик ширины 2 можно разделить на два одинаковых столбика ширины 1); в общем случае, растянутая вдвое скейлинг-функция должна выражаться через сдвиги нерастянутой скейлинг-функции. Этот факт выражается знаменитым уравнением, которое будет второй (и последней) формулой этой статьи:

(2)

В нашем примере это уравнение имеет простейший вид: (столбик ширины 2 есть сумма двух соседних столбиков ширины 1). Заметим, что предельная функция из работы Бэрта-Адельсона тоже удовлетворяет такому уравнению, где - коэффициенты сглаживающего (т.е., понижающего разрешение) фильтра. Но вот сдвиги функции Бэрта-Адельсона не будут ортогональны друг другу.

Оказывается, что если для выполняется уравнение (2) и сдвиги ортогональны друг другу, то возникает совершенно замечательный способ разложения сигналов. А именно, существует еще одна функция, , с такими свойствами:

1. она выражается через сдвиги по формуле, аналогичной (2), но с другими коэффициентами - обозначим их ;
2. у нее ортогональны друг другу не только сдвиги, но и все перемасштабированные версии;
3. эта функция является вейвлетом!

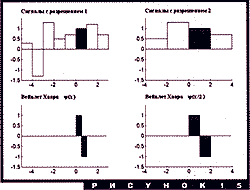
В нашем примере коэффициенты равны 1 и 1, коэффициенты равны 1 и -1. Оказывается, и в общем случае будут перестановкой с измененными знаками, образуют сглаживающий фильтр, - высокочастотный фильтр. Сам вейвлет показан на рис. 15; система его сдвигов и двоичных растяжений и сжатий - это широко известный базис Хаара, построенный еще в начале ХХ века. Для частотно-временного анализа этот базис плохо подходит - частотная локализация у него слабая. А вот, например, в обработке изображений и компьютерной графике он бывает очень полезен - см. статью А. Переберина в этом номере.

Вейвлеты, построенные таким образом, называются ортогональными. Они замечательны в первую очередь тем, что существует очень быстрый алгоритм разложения по ним любого сигнала. Этот алгоритм ("окультуренная" версия алгоритма Бэрта-Адельсона) называется алгоритмом Малла (рис.16). Исходная информация для него - сигнал, заданный с разрешением 1 (на практике - массив длины N). Требуется получить разложение в сумму деталей на более грубых масштабах.

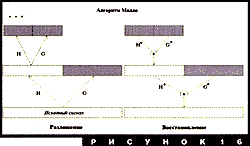
Процедура такова: по исходной информации строится два сигнала (два массива длины N/2). Первый - исходный сигнал, сглаженный фильтром и прореженный вдвое (точный аналог первого этажа пирамиды гауссианов); второй - исходный сигнал, обработанный фильтром и прореженный вдвое (аналог первого этажа пирамиды лапласианов). На языке многомасштабного анализа первый сигнал - вдвое более грубая версия исходного - есть его проекция на подпространство, порожденное сдвигами ; второй (различия между версиями сигнала на масштабе 1 и 2) - проекция на подпространство, порожденное сдвигами . Затем та же процедура применяется к сглаженному сигналу. Возникает два массива длины N/4, и так далее. Результат работы алгоритма - набор высокочастотных деталей, плюс самая сглаженная версия сигнала. Суммарная длина этих массивов равна N (а не 2N, как у Бэрта-Адельсона; это следствие ортогональности).

Процесс восстановления тоже показан на рис. 16. Буквами и обозначается применение транспонированных фильтров - в сущности, та же операция, которую делали Бэрт и Адельсон при вычислении пирамиды лапласианов. На каждом шаге алгоритма размерность массивов удваивается; "сверху вниз" восстанавливаются сглаженные версии сигнала, пока в конце концов не получится исходный сигнал.

Этот алгоритм исключительно прост в реализации, к тому же очень быстр - и на разложение, и на восстановление требуется порядка cN операций, где с - длина фильтра. Напомним, что быстрое преобразование Фурье требует Nlog(n) операций. Формально он дает наиболее компактное представление сигнала в виде разномасштабных компонент - ведь они, по построению, ортогональны, а значит, "некоррелированы". Хочется сразу же применить этот алгоритм к каким-нибудь сигналам. Но где взять фильтры H и G?

Надо отметить, что пары фильтров с такими же свойствами, как у описанных выше H и G, использовались в теории связи задолго до вейвлетов, под названием квадратурных зеркальных фильтров (quadrature mirror filter). С их помощью сигнал разбивался на несколько поддиапазонов, каждый диапазон кодировался и передавался отдельно, а затем все восстанавливалось по тем же формулам, которые использует на каждом шаге алгоритм Малла. Но фильтры эти строились численно, обратимость разложения была, строго говоря, приближенной, а главное - они были "штучными", их умели строить и применять только специалисты. Широкого распространения за пределами довольно специальных задач эти фильтры не имели.

Разбиение на поддиапазоны нужно для того, чтобы выделить (и потом сжать или подавить) высокочастотные детали. Для такой задачи хороши гладкие вейвлеты. К моменту создания теории многомасштабного анализа было несколько примеров ортогональных вейвлетов, более гладких, чем вейвлет Хаара. Найти такие вейвлеты не так просто; считается, что исторически первый пример построил Стремберг (Jan-Olov Stromberg) из университета Тромсе в Норвегии. Но у этих примеров был один практический недостаток - набор коэффициентов был бесконечным. Разумеется, коэффициенты с очень большими номерами были очень малы, но тем не менее... И вот здесь мы произносим имя, которое стало самым знаменитым во всем вейвлетном сюжете: Ингрид Добеши (Ingrid Daubechies).

Именно она первой построила ортогональные вейвлеты, которым соответствуют конечные фильтры. И не просто отдельные примеры: Добеши нашла целую бесконечную серию ортогональных вейвлетов, порожденных двумя (система Хаара), четырьмя, шестью и т. д. коэффициентами. Впоследствии она построила еще несколько таких серий, обладающих различными полезными свойствами. Некоторые скейлинг-функции и вейвлеты из этих серий показаны на рис. 17. Там же приведены частотные характеристики соответствующих фильтров. Именно после ее работы начался взрыв популярности вейвлетов и в математике, и особенно в приложениях. Решив изящную задачу, она дала возможность всем желающим экспериментировать с вейвлетами, сколько душе угодно - причем, что очень важно, на строгой математической основе.

Чтобы связать все сказанное с предыдущим разделом, обратимся к рис. 11. Ортогональные вейвлеты реализуют именно такое покрытие фазовой плоскости "время-частота", как показано на этом рисунке. Другими словами, сигнал раскладывается по октавам, без промежуточных голосов. Тем самым, ортогональный вейвлет-анализ - предельно экономное разложение, в противоположность непрерывному вейвлет-анализу, учитывающему вклад от каждой точки на плоскости (время-частота). Есть и менее экономные варианты дискретных вейвлет-разложений, когда частота меняется не октавами, а включает промежуточные голоса. А что такое коэффициент такого разложения? Это интенсивность "звучания" определенной частоты в определенный момент времени. Совокупность коэффициентов - по сути, нотная запись сигнала!

На этом, объяснение базовых принципов можно закончить. Более подробно математическая сторона дела изложена в статье В.Спиридонова. А мы переходим к обобщениям и примерам использования ортогональных вейвлетов.

Первое обобщение - многомерные базисы (и, соответственно, фильтры). Для того, чтобы получить разложение функции двух переменных (например, цифрового изображения), используются три вейвлета - , , , и одна скейлинг-функция -. Этот базис соответствует многомасштабному анализу со сдвигами и растяжениями вдоль координатных осей. Как устроен алгоритм разложения? Обозначим операции применения фильтров H и G по x и y (с прореживанием). Для изображения, представленного матрицей, будет фильтрацией строк с помощью H, - фильтрацией столбцов с помощью G, и т.д. В этих обозначениях на рис. 18 показана схема разложения двумерного сигнала - фотографии Ингрид Добеши. В одномерном случае мы получали на каждом шаге низкочастотную и высокочастотную компоненты. Низкочастотную мы опять разбивали пополам по частоте, и т.д. В двумерном случае на каждом шаге низкочастотную компоненту разбивают на четыре компоненты, которые можно назвать так: (низкие по х, низкие по у), (низкие по х, высокие по у), (высокие по х, низкие по у), (высокие по х, высокие по у).

Но на плоскости есть бесконечно много других вариантов многомасштабного анализа, связанных со сдвигами и растяжениями вдоль других осей, и с другими коэффициентами. При этом возникают наборы вейвлетов, не являющихся произведениями вейвлетов от икса и от игрека.

Не вдаваясь в эту обширную тему, приведем только один красивый пример. В простейшем случае функций Хаара двумерный вариант получается (по описанной только что схеме) заменой плоских столбиков на пространственные. Скейлинг-функция будет столбиком высоты 1 над единичным квадратом. Так вот, есть другое обощение функций Хаара на двумерный случай. Там будет только один вейвлет (а не три, как у нас), а скейлинг-функция будет единичным столбиком над фрактальным "драконом", показанным на рис. 19. Заметьте, что такими драконами можно замостить всю плоскость, как паркетом. Как ни странно, в многомерном случае типичны именно вейвлеты с фрактальными носителями (т.е., множествами, где они отличны от нуля). Между прочим, эти конструкции имеют прямое отношение к практике, и ими очень серьезно занимается группа вейвлетных исследований в Aware. Дело в том, что вейвлеты-произведения имеют четко выделенные "оси чувствительности" - горизонтальную, вертикальную и две диагональные. Но в реальном изображении могут быть совсем другие выделенные направления, к которым полезно уметь адаптироваться.

Другое важное обобщение - ортогональные вейвлет-пакеты (wavelet packets). В алгоритме Малла на каждом шаге делится пополам низкочастотный диапазон. Но с таким же успехом можно, применяя те же фильтры, построить любое бинарное "дерево диапазонов". Каждому такому дереву соответствует свой набор базисных функций, которые и называются вейвлет-пакетами. Скейлинг-функция в фурье-области покрывает левую, низкочастотную половину диапазона; вейвлет отвечает за правую половину. А вейвлет-пакет может быть сосредоточен, например, на третьей справа "восьмушке" диапазона. Тем самым улучшается разрешение в высокочастотной области. Любое такое разложение имеет длину, равную длине исходного сигнала, который восстанавливается так же быстро, как по традиционному алгоритму Малла. Двумерный вариант этой техники реализуется точно так же, как двумерный алгоритм Малла. Но здесь имеется дополнительная степень свободы - вид самого дерева поддиапазонов. Если речь идет о сжатии, то для разных деревьев коэффициент сжатия одного и того же изображения может отличаться в несколько раз при одинаковом качестве восстановления. Как выбрать оптимальное дерево? Есть алгоритмы, которые для данного изображения довольно быстро строят оптимальное, по некоторму критерию, дерево (обычно говорят об оптимальном базисе, best basis). Правда, критерии, для которых есть такие алгоритмы, не всегда однозначно связаны с визуальным качеством восстановления. Но часто можно найти такое дерево опытным путем для требуемого класса сигналов.

Так поступили, например, в ФБР. В качестве стандартного формата для хранения в компьютерных базах данных коллекции из более чем 30 миллионов отпечатков пальцев был принят усеченный набор коэффициентов разложения по конкретному базису вейвлет-пакетов. Решетка разбиения на частотные диапазоны, определяющая этот формат, показана на рис. 20, там же изображены оригинал отпечатка и его восстановление по 5% и 10% коэффициентов в исходном базисе. Формат JPEG для этой задачи оказался непригодным - из-за блочности, появляющейся при сжатии порядка 20 раз, было сложно определить развилки линий на снимках.

Еще один реальный пример использования вейвлет-пакетов - сжатие данных сейсморазведки. Массив датчиков 200 на 200 (40000 штук), установленных на поверхности, регистрирует подземный взрыв. Каждый датчик записывает пришедшую к нему волну - более семисот плавающих чисел. Возникает 3-мерный массив объемом более 100 мегабайт. Чтобы его сжать в 40 раз (с учетом обратимого кодирования), применялись вейвлет-пакеты по пространственным переменным, и их тригонометрический аналог - по времени. На рисунке 21 изображено (частично) сечение 3-мерного массива плоскостью t=const. Слева - сечение оригинала, справа - сечение восстановленного массива. При внимательном осмотре видны некоторые артефакты, но для многих задач такое качество вполне приемлемо.

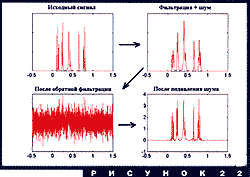
В заключение раздела дадим модельный пример выделения сигнала из шума с помощью ортогональных вейвлетов. На рисунке 22 показаны основные этапы внесения шума и последующей борьбы с ним. Простой сигнал фильтруется, затем к нему добавляется белый шум, после чего выполняется "обратная фильтрация", которая радикально усиливает шум. Сигнал стал неузнаваемым. Но если этот сигнал теперь разложить по ортогональным вейвлетам, занулить или уменьшить некоторые высокочастотные коэффициенты, то даже после обратной фильтрации его вполне можно узнать. Статистики разработали несколько алгоритмов выбора коэффициентов для зануления; оказывается, вейвлет-разложение является оптимальным для борьбы с шумом представлением сигнала.

Обобщения и новые идеи.

В этом разделе мы очень конспективно назовем еще несколько направлений, по которым развивается идеология вейвлет-анализа.

1. Поиск оптимального (для конкретной ситуации) компромисса между непрерывным и дискретным представлением. Ортогональный вейвлет-базис можно рассматривать, как словарь "форм", из которых по определенным правилам набирается заданный сигнал. Но этот словарь можно сильно расширить, взяв более густую сетку в фазовой плоскости. Разложение по такому словарю уже не будет однозначным, но его можно лучше подогнать к сигналу, сделать более устойчивым к помехам. Нахождение коэффициентов - задача оптимизации, но для данного случая есть сравнительно быстрые алгоритмы "квазиоптимизации", самый популярный из которых называется "поиск совпадения" (matching pursuit). Такая методика, кстати, применима не только к вейвлетным словарям.

2. Биортогональный вейвлет-анализ вместо ортогонального. В двух словах это означает, что для разложения по алгоритму Малла используется одна пара фильтров, для восстановления - другая. Биортогональные фильтры построить легче, они более гибкие (например, их можно сделать симметричными, в отличие от ортогональных). Зато возрастает чувствительность к погрешностям при восстановлении.

3. Модная сейчас идея лифтинга (lifting): фильтры H и G, оказывается, всегда можно свести к последовательному применению более коротких фильтров, что ускоряет алгоритм разложения. Если сразу строить их в таком виде, можно лучше адаптироваться к сигналу. С этим связана и другая идея - использовать в разных точках сигнала разные фильтры. Это приводит к отказу от вейвлет-базиса, состоящего из копий одной функции, при сохранении быстрого алгоритма. С помощью этой же идеи строятся вейвлетные фильтры, переводящие целые числа в целые (хотя коэффициенты фильтров - плавающие числа!). Это - хороший препроцессинг при сжатии изображений. Предварительные результаты показывают, что применять обратимое сжатие к результату такого преобразования выгоднее, чем к исходному изображению. Если это подтвердится, на основе вейвлетов может быть создан более эффективный метод обратимого сжатия.

4. Еще одна модная идея - мультивейвлеты. Они возникают, если коэффициенты фильтров H и G не числа, а матрицы. Каждое пространство "деталей" будет порождаться не одним вейвлетом, а несколькими, которые называются мультивейвлетами. Быстрый алгоритм разложения пишется в матричном виде так же, как алгоритм Малла. У мультивейвлетов локализация в пространстве лучше, чем у вейвлетов (при той же гладкости).

Есть много других идей в этой области, которых невозможно даже коснуться в популярной обзорной статье. Некоторые из них освещены в других статьях этого номера. Ознакомившись с приводимым списком литературы и электронных адресов, заинтересованные читатели смогут быстро войти в увлекательный мир вейвлет-анализа. А мне остается только поблагодарить этих читателей за их терпение.

Литература и информация в сети.

Монографии:

C. Chui. An Introduction to Wavelets. Academic Press, 1992.

I. Daubechies. Ten Lectures on Wavelets. SIAM, 1992.

M. Frazier, B. Jawerth, and G. Weiss. Littlewood-Paley Theory and Decompositions of Functional Spaces. AMS, 1992.

Y. Meyer. Wavelets: Algorithms and Applications. SIAM, 1993.

Y. Meyer. Wavelets and Operators. Cambridge University Press, 1993.

M.V. Wickherhauser. Adapted Wavelet Analysis. AK Peters, 1994.

Статьи:

W. Sweldens, P. Schroder. Building your own wavelets at home. In Wavelets in Computer Graphics, pages 15-87. ACM SIGGRAPH Course Notes, 1996.

W. Sweldens. The lifting scheme: A custom-design ocnstruction of biorthogonal wavelets. Journal of Applied and Computational Harmonic Analysis, 3(2):186-200, 1996.

Calderbank, I.Daubechies, W.Sweldens, B.-L.Yeo. Wavelet transforms that map integers to integers. Technical report, Department of mathematics, Princeton University, 1996.

Cайты:

http://cm.bell-labs.com/who/wim/papers/ - страница Вима Свелденса (Wim Sweldens), где можно найти много полезных статей.

http://www.wavelet.org/ - здесь находится электронный вейвлет-дайджест (Wavelet Digest), выходящий с 1992 года, который содержит много информации о статьях, конференциях, людях и т.д.

http://playfair.stanford.edu/~wavelab - здесь находится обширная библиотека вейвлетных программ на языке Matlab. Она называется WAVELAB и распространяется бесплатно.

Пользуясь случаем, хочу поблагодарить разработчиков этой библиотеки за очень качественный продукт. С его помощью подготовлено несколько рисунков для этой статьи.

http://www.mathsoft.com/ - огромный список литературы по теории и приложениям вейвлетов во многих областях науки и техники.