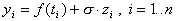
С. А. Терехов. Вейвлеты и нейронные
сети. Лекция для школы-семинара "Современные проблемы нейроинформатики".
МИФИ, Москва, 24-26 января 2001 г.
URL: http://alife.narod.ru/lectures/wavelets2001/index.html
В этом разделе описывается лишь малая толика опубликованных применений компактных волн, при этом, например, не затрагиваются детали метеорологических приложений, подробно описанные в обзоре [Astafieva98], приложения к физике элементарных частиц и методам решения уравнения Шредингера, приложения к анализу и синтезу речи, а также другие направления фундаментальных исследований (анализ фрактальных сигналов, теория аппроксимации и др.). Подробная библиография и публикации по данным вопросам имеется в выпусках электронного журнала Wavelet Digest [Eng00].
Пусть имеется n = 2J+1 наблюдений yi функции f(t) на отрезке [0,1], содержащих "белый" шум:
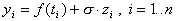
Для очистки сигнала от шума применяется последовательно:
Ниже на Рис.8 приведены результаты подавления шума в модельном ступенчатом сигнале на основе W-преобразования, сплайн-методов и метода Фурье. Такие ступенчатые сигналы характерны, например, для геофизических задач акустического анализа слоистой среды.
Видно, что с использованием W-преобразования достигается более глубокое подавление шума при сохранении структуры сигнала.
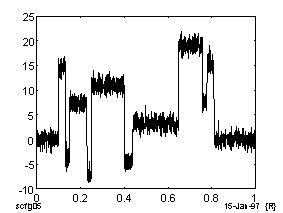 Зашумленный ступенчатый сигнал. |
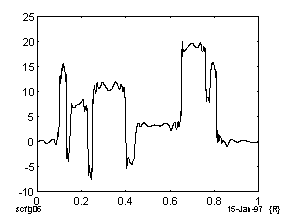 Сигнал, очищенный при помощи W-преобразования. |
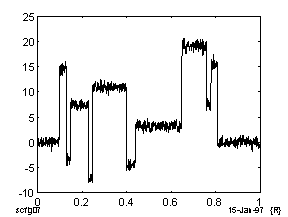 Сигнал, очищенный при помощи сплайн-сглаживания. |
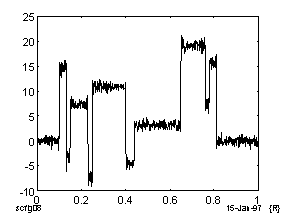 Сигнал, очищенный при помощи обрезания высоких гармоник Фурье. |
Рис. 8. Восстановление ступенчатого сигнала.
Идея нелинейного (порогового) удаления шума состоит в том [Donoho93, Donoho94], что ортогональное W-преобразование "сжимает" сигнал до небольшого числа относительно больших коэффициентов. С другой стороны, "белый" шум в при любом ортогональном преобразовании сохраняет свою структуру и амплитуду. Поэтому пороговое обрезание коэффициентов W-преобразования не влияет на структуру сигнала, сильно понижая шум. W-преобразование близко к "идеальному" проектору, сохраняющему те и только те коэффициенты, для которых сигнал превышает шум.
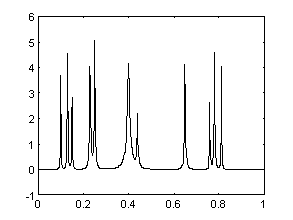
На Рис. 9 приведен пример W-реконструкции реального ЯМР сигнала из шума, при котором не наблюдается уширения пиков, характерного для традиционных линейных методов.
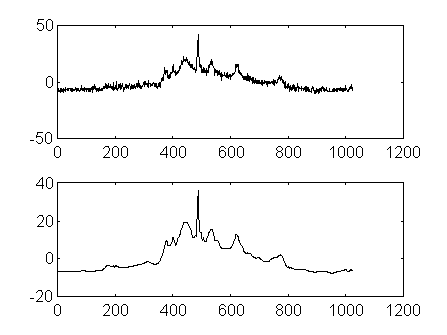
Рис. 9.
Очистка шума в ЯМР сигнале.
Аналогично может быть восстановлен двумерный сигнал - изображение. На Рис 10. изображен портрет Ингрид Добечи (Ingrid Daubechies) - одной из основателей теории W-преобразования. Фрагмент образа был подвергнут зашумлению и восстановлен при помощи W-преобразования с койфлет-функцией, предложенной Добечи [Daubechies88].
 |
   |
Рис. 10. Исходное, зашумленное и восстановленное изображение.
Восстановление из шума, а также описываемое в следующем пункте сжатие информации может использоваться для дальних телекоммуникаций с узкой полосой пропускания.
Рис. 11 иллюстрирует качество восстановления сигнала при "сжатии" его при помощи сохранения заданного количества коэффициентов при ортогональном преобразовании [Donoho93]. В качестве тестового выбран сейсмический сигнал. При сохранении 100 коэффициентов Фурье-преобразования и 100 коэффициентов W-преобразования, более высокое качество последнего проявляется даже при визуальной инспекции.
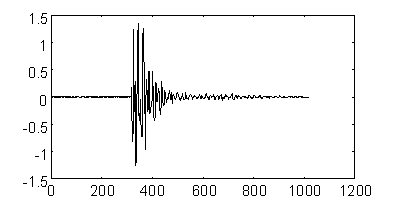
Исходный
сейсмический сигнал.
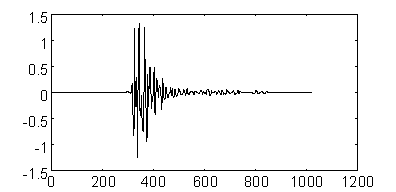
Сигнал,
восстановленный по 100 коэффициентам W-преобразования.
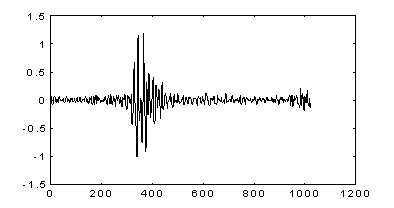
Сигнал,
восстановленный по 100 коэффициентам Фурье-преобразования.
Рис. 11. Сжатие сейсмического сигнала.
В приведенном примере степень сжатия равна 10:1.
Приложения методов глубокой компрессии и качественного восстановления сигналов при помощи W-преобразований охватывают не только область телекоммуникаций, но и емких архивов видео и теле-информации.
На Рис.12 приведен пример использования глубокой компрессии информации для хранения в архиве. Сжатие информации достигает нескольких десятков раз, т.е. в базе данных хранится лишь 2-3 % от исходного объема данных.
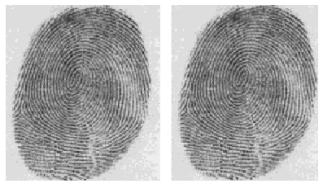
Рис. 12. Реконструкция (справа) отпечатка пальца (слева) после сжатия с
помощью W-преобразования со степенью 26:1. Данные получены из Лос-Аламосской
лаборатории США (http://alife.narod.ru/lectures/wavelets2001/ftp.c3.lanl.gov/pub/WSQ/print_data)
Сжатие информации используется не только для ее хранения или передачи по каналам связи, но и для решения задач анализа и распознавания. При этом значительно сокращается объем вычислений распознающей системы (например, нейронной сети), что ускоряет обработку. Это иллюстрировалось, в частности, и в разделе, посвященном прогнозу временных рядов.
Одним из важных приложений в этой области является анализ радиационных и нейтронных спектров при помощи W-преобразований, с целью контроля и учета делящихся материалов, их классификации (в частности, распознавания материалов, применяемых при разработке систем ядерных вооружений, среди образцов, используемых в энергетике, см., например, http://www.pnl.gov/statistics/research/testban.html).
Одной из важных некорректно-поставленных обратных задач является восстановление сигнала по непрямым измерениям:
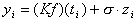
В качестве опосредованно измеряемой величины Kf может служить, например, Фурье-преобразование сигнала f в томографии на основе магнитного резонанса, преобразование Радона в медицинских приложениях, свертки с различными ядрами в спектроскопических измерениях и т.п. В этих случаях речь идет о восстановлении W-коэффициентов из произвольного (не "белого") шума.
В качестве примера рассмотрим задачи численного дифференцирования и восстановления дискретной свертки.
Типичной при проведении физических экспериментов является задача восстановления дискретного сигнала x из наблюдений его зашумленного кумулянта
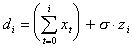
Конечные разности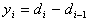 
приводят к выражению
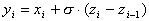. Последнее эквивалентно непосредственному
наблюдению сигнала с негауссовым шумом. Результат применения разностного
численного дифференцирования измерений d является, очевидно,
неудовлетворительным (см Рис. 13).
W-преобразование в данной задаче используется так же, как и при выделении сигнала из шума, но с порогом, зависящим от уровня разрешения W-коэффициентов. При этом порог для высоких частот значительно выше, чем для низких частот.
Результаты дифференцирования с использованием W-преобразования приведены на Рис.13.
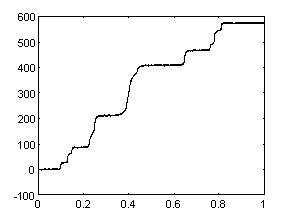
 Исходный сигнал. |
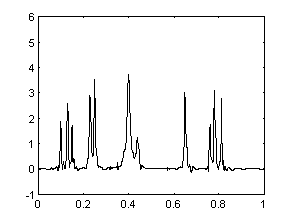
 Зашумленный кумулянт (наблюдения). |
 Сигнал, восстановленный из кумулянта при помощи W-преобразования. |
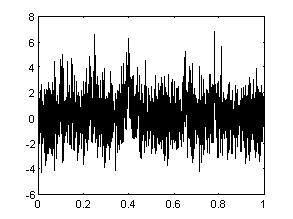 Результат конечно-разностного дифференцирования. |
Рис. 13. Численное дифференцирование.
В многих схемах передачи сигнала приемник регистрирует не сам сигнал, а его свертку, подверженную шуму.
Пусть наблюдается величина
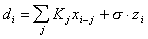
Формальное обращение свертки K-1 приводит к эквивалентному наблюдению сигнала с негауссовым шумом (K-1 z).
W-преобразование с порогом, зависящим от частоты, дает удовлетворительное восстановление сигнала из свертки (Рис. 14).
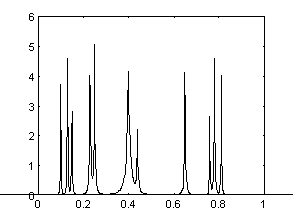 Исходный сигнал. |
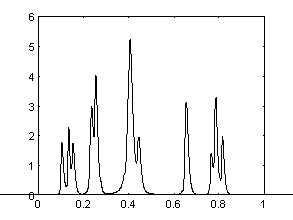 "Размытый" при свертке сигнал (наблюдения). |
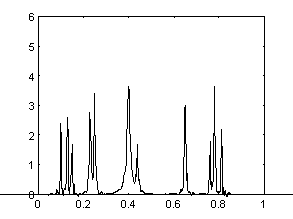 Обращение свертки при помощи W-преобразования. |
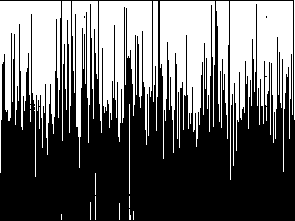 Результат формального применения обратного оператора свертки. |
Рис. 14. Обращение свертки.
Удачность выбора базиса в виде компактных волн привела к ряду предложений по построению эффективных вариационных методов (в частности, метода Галёркина [Leaf95, Fletcher88, Shann91]) решения уравнений в частных и полных производных. В случае вейвлетов, отличных от нуля на отрезке, пространственное представление решения строится аналогично методу конечных элементов, при этом для получающейся системы О.Д.У. применяются стандартные адаптивные методы (например, методы Адамса или метод Гира [Fletcher88]).
Диссертационная работа [Shann91] посвящена развитию вейвлет-методов для обыкновенного уравнения второго порядка на отрезке, с граничными условиями Дирихле, Неймана и смешанными:
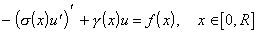
Решение строится путем проекционного разложения по компактным волнам специального вида, образующим полную систему на отрезке (в пространстве функций, интегрируемых с квадратом). Для тестовых задач сходящиеся решения получены для 3-4 элементов базиса.
В работе [Leaf95] предложена методика решения гиперболических уравнений (на примере уравнений Буссинеска, используемых в геофизических приложениях), разработанная в Аргоннской Национальной Лаборатории США. В данной работе сравниваются псевдо-спектральный метод Фурье, разностный метод с перешагиванием (leap-frog) и вариационный метод на основе W-преобразования. Характерные результаты расчетов разрывного течения приведены на Рис. 15 (приведен фрагмент рисунка, заимствованного из работы [Leaf95], в области сильного разрыва).
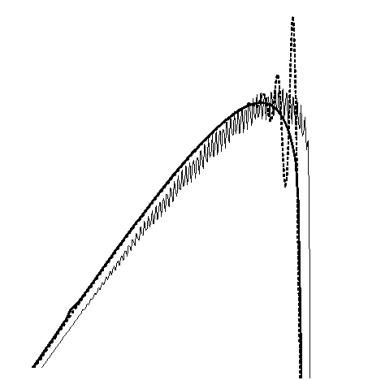
Необходимо отметить, что приведенные результаты качества представления разрывного решения не являются всеобщими, однако они указывают на необходимость дальнейшего совершенствования методов W-преобразований для численных методов.
Компактные волны представляются удобным и естественным инструментом для исследований электромагнитных явлений[Kaiser94], поскольку уравнения Максвелла (как и вейвлеты) инвариантны относительно перемещений и изменений масштаба. При этом формализм W-преобразований позволяет сформулировать физические принципы волновых явлений и вопросы обработки сигналов на едином языке. В книге [Kaiser94] построен универсальный вейвлет-базис для решений уравнений Максвелла в свободном пространстве.
В работе [Pierce96] вейвлет-представление было успешно применено для моделирования прохождения оптического импульса в нелинейной среде. При этом численно решалось нелинейное уравнение Шредингера для слабо меняющейся амплитуды электрического поля в волноводе:
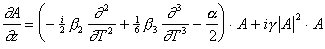
Данное уравнение учитывает групповую дисперсию, фазовую само-модуляцию и поглощение волны. Решения для распространения гауссового пакета, приведенные в [Pierce96], получены на основе метода расщепления линейного и нелинейного операторов в правой части, с разложением решения по вейвлет-базису Добечи.
Метод W-разложения сравнивался с традиционно используемым разложением Фурье, при этом, при одинаковой точности результатов, схема на основе W-разложения имеет вычислительную сложность O(N), в то время, как Фурье-схема - O(N log N).
Исследование метеорологических и климатических процессов в последнее время особенно актуально [Astafieva98, Zubair93]. При этом возрастает как объем9 обрабатываемых данных [Acheroy94], так и сложность моделируемых процессов [Zubair93].
В обзоре [Astafieva98] описаны применения методов компактных волн к анализу климатических временных рядов. Исследованы долговременные (на масштабах (10-100 лет) аномалии температур Южного и Северного полушария.
В работе [Zubair93] методы компактных волн применены для анализа явлений атмосферной турбулентности, которая характеризуется локализованными событиями, происходящими на широком диапазоне масштабов. Вейвлет-преобразование является инструментом, напрямую нацеленным на описание таких явлений. В этой работе используется двумерный аналог G2-вейвлета (описанного во вводном разделе):
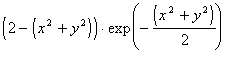
На Рис. 16 приведены изображения турбулентной струи (полученные в модельных экспериментах при помощи теневой фотографии) и результаты W-анализа для двух различных пространственных масштабов. Компактно волновое представление экспериментальных данных дает наглядную и количественно интерпретируемую картину явлений разных масштабов.
 |
 |
 |
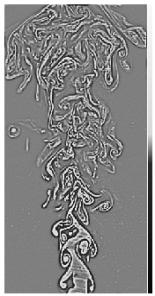Рис. 16. Теневая фотография турбулентной струи (слева) и ее W-преобразование на двух различных пространственных масштабах.
Коэффициенты W-преобразований используются в [Zubair93] для построения статистических моделей турбулентности. Оригинальный подход к исследованию турбулентных течений методами вейвлет анализа предложен в новом совместном проекте ФИАН и ВНИИТФ для Международного научно-технического центра (http://www.istc.ru/).