Источник : http://www.chipnews.ru/html.cgi/arhiv_i/00_01/stat-45.htm

Стивен Маас

Что надо знать о методе анализа на основе рядов Вольтерра

    B настоящее время пользователям наиболее распространённых программ моделирования электронных схем стал доступен метод анализа на основе рядов Вольтерра. При моделировании схем со слабой нелинейностью он предлагает более высокую скорость и точность анализа, чем популярный метод гармонического баланса. Для получения оптимальных результатов при использовании метода рядов Вольтерра необходимо чёткое понимание основных методов и способов моделирования нелинейных схем.

Введение

    Tот, кто уже использовал какую-либо программу нелинейного анализа электронных схем, вряд ли догадывается, что имеется масса других способов проведения такого вида анализа. Большинство программ моделирования ВЧ и СВЧ схем базируются на методе гармонического баланса. Этот метод предлагается как средство решения задач любого рода, с чем он, согласно установившемуся мнению, успешно справляется.

    На практике имеются задачи, с решением которых метод гармонического баланса справляется не совсем хорошо. К этой области можно отнести задачи анализа схем со слабо выраженной нелинейностью или схем, на вход которых подаются сигналы малого уровня, например, моделирование малосигнального усилителя на полевом транзисторе. Можно было бы предположить, что анализ такой малосигнальной схемы не вызовет особых затруднений, но на практике всё оказывается намного сложнее, так как большинство мо-делей твердотельных устройств не предназначены для анализа методом гармонического баланса, а сам метод весьма чувствителен к едва уловимым ошибкам, громоздок и раздражающе медленен.

    Анализ на основе рядов Вольтерра является наиболее подходящим методом для моделирования схем со слабой нелинейностью. Он идеально подходит для оценки интермодуляционных искажений (IM), анализа схем, работающих в линейном режиме (то есть, ниже точки компрессии усиления по уровню -1 дБ), и схем, выполняющих преобразование амплитудной модуляции в фазовую (AM-to-PM). Анализ на основе рядов Вольтерра для такого рода задач предлагает значительно большую точность и скорость, на несколько порядков превышающие получаемые при использовании метода гармонического баланса. Кроме того, он хорошо интегрируется с распространёнными методами анализа линейных схем и даёт возможность одновременной оптимизации нелинейных эффектов и коэффициентов шума, передачи и отражения. С учётом всех перечисленных преимуществ, этот метод может считаться оптимальным для анализа схем со слабой нелинейностью.

    К сожалению, до настоящего момента ни одна полнофункциональная программа моделирования нелинейных электронных схем не предлагала пользователям метод анализа на основе рядов Вольтерра. Относительно новый программный продукт компании Applied Wave Research, называющийся VoltaireXL [1] и входящий в состав интегрированного пакета Microwave Office, предполагает широкое использование этого метода. Теперь, когда анализ на основе рядов Вольтерра стал доступен всем желающим, весьма полезно будет оценить его функциональные возможности, преимущества и неудобства, а также показать, как наилучшим образом использовать его для разработки и оптимизации высокочастотных и сверхвысокочастотных устройств.

Что такое анализ на основе рядов Вольтерра?

    Mетод анализа на основе рядов Вольтерра является одним из самых старых методов нелинейного анализа схем, предложенным ещё в 60-х годах. Он был раз-работан как метод анализа систем уравнений Норбертом Вейнером (Norbert Weiner), который использовал работу итальянского математика Вито Вольтерра (Vito Volterra), чтобы получить входные и выходные соотношения для компонентов нелинейных систем уравнений. Вейнер показал, что так называемый функциональный ряд Вольтерра может быть использован для описания таких систем, пока нелинейность в них не проявлялась слишком сильно.

    Позднее, эта идея была применена к анализу электрических схем. К 60-м годам нашего столетия борьба с искажениями в радиоприёмных системах превратилась в серьёзную проблему, и академическая наука начала поиск способов лучшего понимания возникающих искажений. Большая часть из этих исследований была выполнена в научном центре Rome Air Development Center в США, и завершилась опубликованием нескольких классических научных трудов [2-4]. Теория Вольтерра, казалось, была идеальным математическим инструментом. Тем не менее, параллельно велась работа по дальнейшему улучшению линейных свойств твердотельных устройств, и в этой области были сделаны значительные успехи, отодвинувшие на второй план актуальность нелинейного анализа. Такая ситуация продолжалась приблизительно двадцать лет. Используемые сегодня системы связи снова стали критическими к возникающим в них искажениям, а значит, возросла необходимость в проектировании и оптимизации схем с целью минимизации проявляющихся паразитных эффектов.

    К большому удовольствию читателей, в данной статье не будет приведено скучное и рутинное описание функционального ряда Вольтерра. К счастью, для плодотворного использования метода рядов Вольтерра нет необходимости в детальном понимании всей заложенной в него математики. Фактически, алгоритмы, используемые в его программной реализации, весьма отличаются от функционального ряда Вольтерра как такового, и знание базовой математики обеспечивает лишь некоторую интуитивную часть понимания реализации метода. Намного важнее понять, как получить от метода максимальную точность и как остаться в пределах математических ограничений метода, чтобы полученные результаты были достоверными.

    При анализе методом рядов Вольтерра производится расчёт уровней различных интермодуляционных составляющих, чаще называемых продуктами преобразования. Как правило, наибольший интерес представляют получаемые при двухтональном воздействии интермодуляционные составляющие третьего порядка, рассчитываемые по формуле 2f2 – f1, где f1 и f2 — частоты двух сигналов, подаваемых на анализируемое устройство. Между тем, анализ на основе рядов Вольтерра не ограничивается анализом интермодуляционных искажений. Кратные гармоники сигналов, продукты AM-to-PM преобразования и многое другое могут быть описаны как результат смешивания частот сигналов возбуждения. Порядок продукта преобразования или интермодуляционной составляющей определяется просто как сумма коэффициентов частот. То есть, если продукт преобразования получен по формуле:

f = mf1 + nf2 + pf3 + ... ,

 (1)

    то его порядок будет равен:

О = |m| + |n| + |p| + ... .

 (2)

    Заметим, что некоторые продукты более высоких порядков могут совпадать по частоте с продуктами низких порядков, например, если продукт преобразования третьего порядка рассчитывается по формуле:

f = f + f – f.

 (3)

    Поскольку в преобразовании здесь участвуют три частоты, то это продукт преобразования третьего порядка. Однако, конечное значение совпадает с фундаментальной частотой. Может показаться странным, но это важный продукт: интерференция между этой составляющей и полезным фундаментальным продуктом преобразования может использоваться для определения точки компрессии или параметров AM-to-PM преобразования. Аналогичным образом, кратные гармоники сигнала можно представить как:

2f = f + f ,

 (4)

    то есть, сигнал как бы смешивается сам с собой.

Рис. 1. Нелинейный резистор может быть представлен как линейный, соединенный параллельно с двумя "нелинейными" источниками тока. Параметры этих источником могут быть выбраны таким образом, чтобы каждый определял один порядок и зависел от напряжений низших порядков

    Наиболее общая реализация анализа на основе рядов Вольтерра базируется на так называемом методе нелинейных токов. При этом подходе, каждый нелинейный элемент схемы преобразуется в линейный элемент с множеством параллельно включённых источников тока. Рассмотрим, например, эквивалентную схему нелинейного резистора, изображённую на рис. 1. Нелинейные свойства элемента полностью определяются дополнительными источниками тока. Ток очередного порядка нелинейности определяется напряжением на элементе при учёте всех нелинейностей меньшего порядка, так что все токи рассчитываются через рекуррентные соотношения. Сначала рассчитывается напряжение элемента первого порядка, затем ток второго порядка. После этого в качестве сигнала возбуждения на схему подаётся ток второго порядка, и получается напряжение элемента второго порядка. Ток третьего порядка получается из напряжений первого и второго порядков, и этот процесс повторяется, пока не будут получены продукты преобразования всех интересующих порядков. Предположим, например, что нам необходимо рассчитать продукт преобразования, получаемый по формуле 2f2 – f1. Вполне очевидно, что схема должна сначала быть проанализирована на частотах f1 и f2. Затем программа моделирования анализирует схему на частотах продуктов второго порядка, 2f2 и f2 – f1. Наконец, она получает все части, необходимые для расчёта интересующего нас продукта преобразования третьего порядка 2f2 – f1. В итоге, получается решение на нужной нам частоте, а также линейные характеристики и пара продуктов преобразования второго порядка, выступающих как побочные.

    При анализе на основе рядов Вольтерра моделируемая схема описывается как комбинация линейных и нелинейных элементов. Линейные элементы описываются обычным образом: резисторы, конденсаторы, линии передачи и так далее. Нелинейные элементы описываются разложением в ряд Тейлора их вольтамперной (I/V) или кулонвольтной (Q/V) характеристик. Например, нелинейный резистор, имеющий вольтамперную характеристику:

I = fR(V),

 (5)

    описывается разложением в ряд Тейлора вблизи рабочей точки смещения (V0, I0):

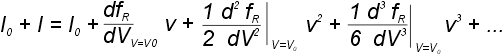(6)

    где i — ток, а v — напряжение в режиме малого сигнала. Нас интересуют только малосигнальные значения v и i, а производные в любой точке представляют собой не что иное как константы. Поэтому, в определённой точке смещения ряд (6) может быть написан в виде:

i = g1v + g2v2 + g3v3 + ...

 (7)

    Заметим, что g1 = 1/R, где R — линейное сопротивление в рабочей точке смещения в малосигнальном режиме.

    Разложение в ряд Тейлора имеет силу только для небольших отклонений от его центрального параметра, так что выражение (7) для тока в малосигнальном режиме верно только когда v << V0 и i << I0. Это требование является фундаментальным ограничением метода анализа на основе рядов Вольтерра: он работает только когда входной сигнал мал настолько, что значения производных вольтамперной характеристики остаются постоянными при соответствующем отклонении постоянного напряжения и тока от рабочей точки смещения. Мы говорим, что такой элемент схемы имеет слабую нелинейность, то есть нелинейность должна быть слаба, а входное воздействие мало настолько, что возможно представление вольтамперной или кулонвольтной характеристики элемента в виде разложения в ряд Тейлора1).

    На практике это означает, что уровень входного сигнала должен быть таким, чтобы анализируемый элемент работал значительно ниже его точки насыщения. По этой причине, анализ на основе рядов Вольтерра не подходит для анализа смесителей, умножителей частоты, усилителей мощности, работающих в режиме насыщения, и других подобных им устройств. Тем не менее, он идеально подходит для анализа интермодуляционных искажений в малосигнальных усилителях, электронных коммутаторах, фазовращателях, аттенюаторах и подобных им схемах.

Достоинства и недостатки метода анализа на основе рядов Вольтерра

    Bыражение (7) выглядит достаточно просто и не требует больших усилий для понимания. Менее очевидно то, что оно может быть полностью определено в частотной области, причём нет необходимости ни в каких повторяющихся преобразованиях Фурье, неизбежных при анализе методом гармонического баланса. В результате, анализ на основе рядов Вольтерра не ограничен числовым диапазоном многочастотного преобразования Фурье, а так как нет никаких многократно повторяющихся объёмных вычислений, он выполняется чрезвычайно быстро. При этом большая часть времени вычислений определяется линейным анализом схемы, а время, требуемое для расчёта нелинейных токов, постоянно и незначительно.

    Так как метод анализа на основе рядов Вольтерра в значительной степени состоит из линейных расчётов, его можно очень легко объединить с анализом схемы в линейном режиме. Это свойство делает возможным одновременную оптимизацию интермодуляционных искажений, шумов, коэффициента усиления и многих других параметров линейной схемы. При проведении таких вычислений с применением метода гармонического баланса потребуется многократное переключение между модулями оптимизации в программах линейного моделирования и моделирования методом гармонического баланса, что делается неуклюже и медленно, а также сопровождается многочисленными ошибками. При анализе на основе рядов Вольтерра всё делается чрезвычайно легко.

    Самым большим недостатком метода анализа на основе рядов Вольтерра являются случающиеся время от времени затруднения в решении в случае, когда было превышено требование на малую нелинейность. Есть несколько характерных признаков, по которым можно определить, что начальные условия вышли за рамки допустимых. Например, при увеличении сигнала интермодуляционные составляющие не входят в насыщение, а продукты преобразования на фундаментальных частотах насыщаются слабо. Здесь как никогда полезен некоторый практический опыт. Любой, кто занимался измерением параметров малосигнальных усилителей, приблизительно знает значения сигналов, при которых уровни интермодуляционных составляющих начнут насыщаться, а значит, надо только оставаться несколько ниже этих значений.

    Наконец, следует отметить то, что методы гармонического баланса и рядов Вольтерра удачно дополняют друг друга. Задачи, которые нельзя решить методом на основе рядов Вольтерра, можно без труда решить методом гармонического баланса, и наоборот. И естественно отсюда следует, что конкурентоспособная современная программа нелинейного моделирования электронных схем должна обязательно включать в себя оба метода.

Почему все-таки не использовать метод гармонического баланса?

    Aнализ схем с малой нелинейностью методом гармонического баланса — процесс весьма обманчивый. С одной стороны, кажется, что всё работает хорошо: вы нажимаете кнопку, расчёт пошёл, метод имеет сходимость, и получились весьма правдоподобные результаты. К сожалению, этот результат, как правило, неверный, и происходит это по одной или более из трёх причин: из-за неполной сходимости метода, числового шума и сложности анализируемой схемы.

    При анализе методом гармонического баланса программа моделирования оценивает полученное решение и последовательно улучшает его. В какой-то момент она может сделать вывод, что полученное решение достаточно точное, и остановить итерационный процесс. Как правило, имеется несколько различных способов определения степени завершённости расчёта, а программа моделирования имеет установленный по умолчанию критерий, который пользователь может изменять по своему усмотрению. Если этот критерий задан недостаточно жёстко, то ошибка, полученная при завершении процесса расчёта, может быть слишком велика и даже превышать уровень интересующих нас интермодуляционных составляющих. В итоге мы получаем неправильный результат из-за недостаточной сходимости метода.

    Предположим, например, что прерывание процесса происходит, когда самая максимальная погрешность расчёта любого продукта преобразования составляет 10-5 А (общий параметр). Значение тока интермодуляционных составляющих с уровнями порядка 80 дБ составляет приблизительно 10-6 А. То есть, погрешность расчёта тока, полученная в ходе моделирования, в десять раз превышает реальный уровень сигналов. А ведь это означает итоговую ошибку на 20 дБ!

    Выход из этой ситуации напрашивается сам собой: надо более жёстко задать критерий сходимости. Однако, здесь кроется другой подводный камень: критерий сходимости не может быть задан произвольно (слишком жёстко), так как большой объём численных вычислений, выполняемых при использовании метода гармонического баланса, снижает численную точность, иначе говоря, генерирует числовой шум. Операция преобразования Фурье, хотя и не является самой интенсивной частью процесса численного расчета, является источником непропорционального по уровню числового шума. Если вы попытаетесь установить критерий сходимости ниже уровня шума (например, зададите максимальную погрешность расчёта тока на уровне 10-12 А, в то время, как шум имеет уровень порядка 10-10 А), процесс расчёта просто не будет сходиться. Таким образом, вы оказываетесь между двух огней — низким уровнем рассчитываемых сигналов, с одной стороны, и высоким уровнем числового шума, с другой. Такого рода неприятности никогда не происходят при анализе на основе рядов Вольтерра, потому что этот метод не является итерационным и не нуждается в численном вычислении преобразования Фурье. А значит, получается числовой диапазон решения.

    Более серьёзная проблема состоит в том, что некоторые модели устройств, используемые в программах анализа методом гармонического баланса, абсолютно не подходят для моделирования слабых нелинейностей. Критерием правильности используемой модели здесь является следующее утверждение (оно следует из выражения (6)): модель должна позволять с достаточной точностью рассчитывать кратные производные вольтамперной (I/V) или кулонвольтной (Q/V) характеристики устройства. Лишь немногие из большинства доступных моделей для метода гармонического баланса позволяют это, а все остальные требуют весьма осторожного подхода к заданию параметров. С другой стороны, модели, предназначенные для анализа на основе рядов Вольтерра, автоматически выполняют это требование.

    По сути, метод гармонического баланса разрабатывался для анализа схем, работающих с большими сигналами, а метод рядов Вольтерра, наоборот, для малосигнальных схем. Разве не имеет смысл объединить их в одной программе моделирования?

Cовременная программа моделирования нелинейных электронных схем

    Первой коммерческой программой моделирования на основе рядов Вольтерра был пакет C/NL2, разработанный компанией Nonlinear Technologies и распространяемый организацией Artech House Publishers. Пакет C/NL2 был достаточно дешев и имел весьма ограниченные возможности: анализируемая схема вводилась в виде списка соединений, отсутствовал набор моделей и функций, необходимых для проектирования современных гибридных и монолитных интегральных схем. Пакет C/NL2 включал метод анализа на основе рядов Вольтерра, но не включал метод гармонического баланса. Тем не менее, он занял свою экологическую нишу и нашёл своих пользователей.

    Недавно вышедший пакет моделирования Microwave Office производства компании Applied Wave Re-search включает модуль VoltaireXL, использующий и метод гармонического баланса, и метод на основе рядов Вольтерра. Это первая доступная широким массам разработчиков программа анализа СВЧ-схем, интегрирующая метод рядов Вольтерра. Пакет Microwave Office также объединяет модуль полного электромагнитного (EM) моделирования и модуль анализа линейных схем под управлением единого графического интерфейса пользователя, что делает его весьма мощным инструментом для проектирования ВЧ и СВЧ устройств.

    Модуль VoltaireXL имеет ряд существенных преимуществ по сравнению с пакетом C/NL2. Подобно большинству распространённых сегодня программ анализа схем, архитектура пакета C/NL2 была задумана во времена, когда память была слишком дорога. По этой причине, пакет C/NL2 анализировал полную схему на каждой отдельной частоте, печатал результаты, очищал память и многократно использовал её для анализа в следующей частотной точке. В модуле VoltaireXL все вычисления векторизованы, например, расчёт матрицы полной проводимости линейной схемы на каждой отдельной частоте производится единожды, сохраняется в памяти и затем многократно используется, пока какой-либо элемент схемы не будет изменён. Это свойство делает пакет VoltaireXL весьма быстродействующим и позволяет производить ручную настройку больших схем с нелинейными элементами в реальном масштабе времени. Аналогичным образом могут быть кэшированы параметры моделей, так что сложные модели могут не пересчитываться каждый раз при изменении не относящегося к ним параметра. Все эти функциональные возможности стали доступны благодаря использованию современного объектно-ориентированного подхода к разработке программы.

    Такой подход делает возможным тесную интеграцию между различными модулями программы моделирования. Например, объёмная структура, построенная и проанализированная модулем полного электромагнитного моделирования, становится обычным элементом (подсхемой) в программе моделирования электронных схем, и может быть внедрена в схематический модуль, подобно любому другому элементу. Кроме того, после векторизации характеристик EM-структуры пересчёт производиться не будет, пока какой-либо её параметр или топологиче-ский элемент не будет изменён.

    Все модели, применённые в пакете VoltaireXL и предназначенные для анализа методом гармонического баланса, могут использоваться программой моделирования на основе рядов Вольтерра. Эта программа получает производные вольтамперных (I/V) и кулонвольтных (Q/V) характеристик нелинейных моделей, необходимые для расчёта коэффициентов разложения в ряд Тейлора характеристик, аналитическим путём без использования метода конечных разностей (такая методика известна давно, но до сих пор широко не использовалась). Таким образом, любое нелинейное устройство может быть проанализировано или методом рядов Вольтерра, или методом гармонического баланса. Аналогично, могут быть рассчитаны линейные характеристики нелинейных устройств, так как программа моделирования линеаризует каждый транзистор или любой другой нелинейный элемент в его рабочей точке. Процесс этот аналогичен анализу частотных характеристик программы SPICE, но, в отличие от SPICE, здесь одна и та же модель используется и для линейного, и нелинейного анализа, что гарантирует связность между двумя разновидностями моделирования. Ниже приведены несколько примеров, ярко демонстрирующих возможности, предлагаемые комбинацией современного программного обеспечения для проектирования и технологии анализа нелинейных устройств. Хочется верить, что в ближайшем будущем эти возможности будут доступны во всех программах моделирования электронных схем.

Примеры анализа методом рядов Вольтерра

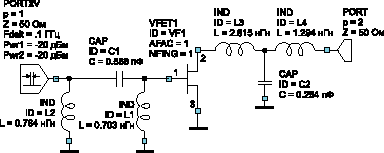
    На рис. 2 показан малосигнальный однокаскадный усилитель диапазона 7–11 ГГц, состоящий из одного полевого транзистора (FET) и типовых прототипов согласования на сосредоточенных элементах. Модель полевого транзистора FET состоит из линейной эквивалентной схемы и одного нелинейного управляемого источника тока, чего, как правило, достаточно для правильного моделирования обычного полевого транзистора с барьером Шоттки (MESFET) для анализа методом рядов Вольтерра.

Анализ данного усилителя проводился методом рядов Вольтерра

Рис. 2. Анализ данного усилителя проводился методом рядов Вольтерра. Практически все элементы эквивалентных согласующих цепей были реализованы как распределенные

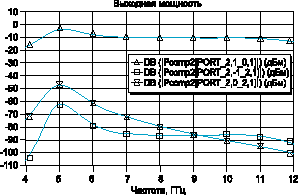
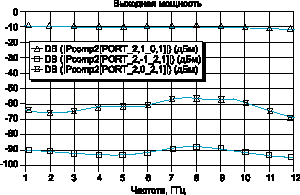
    На рис. 3 показаны частотные зависимости усиления и уровня интермодуляционных составляющих третьего порядка. Расчёт методом рядов Вольтерра проводится настолько быстро, что стало возможным настраивать схему в режиме реального времени, выполняя при этом нелинейный анализ. В результате, нелинейная схема может быть оптимизирована вручную или с помощью автоматического оптимизатора почти так же быстро, как и линейная.

Рассчитанные зависимости уровней мощности

Рис. 3. Рассчитанные зависимости уровней мощности основной (D), второй и 2f2 - f1 гармоник сигнала на выходе СВЧ усилителя в диапазоне 7-11 ГГц при уровне входного сигнала -20дБм

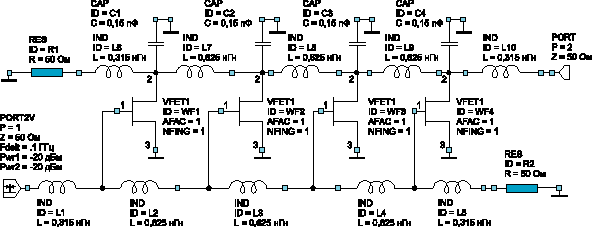
    На рис. 4 показан усилитель бегущей волны на четырёх полевых транзисторах. Здесь также рассчитывались усиление и уровни интермодуляционных составляющих (рис. 5). Настройка этого усилителя в режиме реального времени возможна и при большем числе транзисторов.

Усилитель бегущей волны диапазона 1-12 ГГц на четырех полевых транзисторах

Рис. 4. Усилитель бегущей волны диапазона 1-12 ГГц на четырех полевых транзисторах. Стоковые конденсаторы выравнивают фазовую скорость в затворной и токовой цепях, что позволяет значительно расширить полосу пропускания усилителя

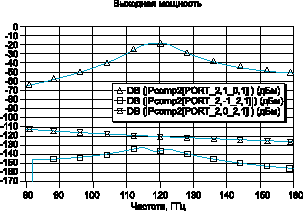
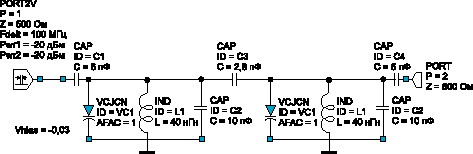
    Метод анализа на основе рядов Вольтерра применим и к пассивным устройствам. На рис. 7 показан варакторный преселектор метрового диапазона. Рассчитанные характеристики изображены на рис. 6. Перестройка преселектора осуществляется изменением напряжения смещения на варакторных диодах. Следует отметить, что худший уровень интермодуляционных составляющих третьего порядка получается в области нижних частот, где варактор смещается в область большей нелинейности его кулонвольтной (Q/V) характеристики.

Рассчитанные зависимости уровней мощности

Рис. 5. Рассчитанные зависимости уровней мощности основной, второй и 2f2 - f1 гармоник сигнала на выходе СВЧ усилителя бегущей волны в диапазоне 1-12 ГГц при уровне входного сигнала -20 дБм


Рассчитанные зависимости уровней мощности

Рис. 6. Рассчитанные зависимости уровней мощности основной, второй и 2f2 - f1 гармоник сигнала на выходе варакторного перестраиваемого фильтра метрового диапазона при уровне входного сигнала -20 дБм

    Также интересен тот факт, что зависимости уровней интермодуляционных составляющих являются плоскими по сравнению с передачей по основной гармонике. Если учесть, что данный преселектор используется для подавления внеполосных сигналов, то мощный мешающий сигнал может стать серьёзным источником искажений, возникающих в нём самом.

Варакторный перестраиваемый фильтр метрового диапазона

Рис. 7. Варакторный перестраиваемый фильтр метрового диапазона

Заключение

    Анализ на основе рядов Вольтерра может применяться для схем, содержащих устройства со слабой нелинейностью. Современные программы моделирования электронных схем могут объединять такой метод с анализом шумов и линейных схем, что позволит настраивать даже достаточно сложные схемы практически в реальном масштабе времени. Благодаря своей совместимости с другими методами анализа, метод рядов Вольтерра должен стать неотъемлемой частью всех современных программ моделирования электронных схем.

Литература

  1. Applied Wave Research, 1960 E. Grand Ave., El Segundo, California, 90245, USA.
  2. J.W. Graham and L. Ehrman, Nonlinear System Modeling and Analysis with Applications to Com-munications Receivers, Rome Air Development Center Technical Report No. RADC-TR-73-178, 1973.
  3. J.J. Busgang, L. Ehrman, and J.W. Graham, Analysis of Nonlinear Systems with Multiple Inputs, Proc. IEEE, vol. 62, p. 1088, 1974.
  4. D.D. Weiner and J.F. Spina, Sinusoidal Analysis and Modeling of Weakly Nonlinear Circuits, Van Nostrand, New York, 1980.

    «Applied Wave Research», 1999 г.
    Перевод Ю. Потапова