Вся эта входная информация будет, обрабатываться математическими моделями.
Наиболее распространенным методом описания результатов эксперимента возникла "кривая", то есть график, который изображает, как в условиях заданного эксперимента от пробы к пробе изменяются характеристики контролируемого или группы контролируемого. В качестве "функции успеваемости" предлагались разнообразнейший аналитические функции, в том числе гипербола, функция экспоненциального роста, арктангенс. Однако ни одна из этих функций не была получена на основе фундаментальной теории обучения.
О.Щукаревым было выведено
следующее уравнение:
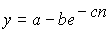 ,
,
где 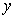 - успевемость, обусловленное числом правильных воспроизведений (успехов) за единицу времени;
- успевемость, обусловленное числом правильных воспроизведений (успехов) за единицу времени;
n - число объма за единицу времени;
а - граница успеваемости при п ® ∞; b и с - константы.
Т.Робертсоном было предложенно
уравнение вида:
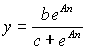
где у - успеваемость; п - число объма за единицу времени;
А = аb, а, с -константы (параметры контролируемого); b - граница успеваемости при n ? ∞.
Л.Терстоун предложил следующую
формулу (так называемый гиперболический закон успеваемости):
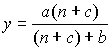 ,
,
где у - успеваемость; п
- число объма; а и с - константы; b -скорость объёма.
Стахостимческие модели
Халла и Терстоуна интерпретируются. Так, модель Халла приобретает вид:
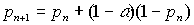 ,
,
где рn
- вероятность приобретения навыка в п-ом времени; 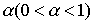 - константа.
- константа.
В модели Терстоуна величина у
интерпретируется как вероятность приобретения навыка рn:у = 0 при п = 1 и у ->
1 при п ® ¥ .
Уравнение Терстоуна приобретает вид:
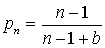
где b - скорость обучения.
Пусть в момент времени
t=0 информация обработана,
а при t>0 ему даётся дополнительный материалу. Если в момент t = tконтролируемый не успевает обработать материал, то t отвечает времени не успеваемости. Предполагается, что время t -непрерывная случайная величина с функцией распределения
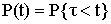 .
.
В случае экспоненциального
распределения
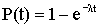 ,
,
где λ - интенсивность не успеваемости. Среднее время не успеваемости равняется 1/λ. Вероятность успеваемости обработки материала лежит в интервале (0, t) 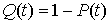 .
.
Интенсивность не успевания λ(t) имеет следующее значение. Величина λ(t)Δt представляет собой вероятность того, что контролируемый успеет обработать материал в интервале времени (0,t) не успеет обработать в интервале времени (t, t + Δt).
В случае маленьких Δt получаем:
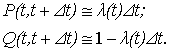
Для описания процесса не успеваемостия, кроме экспоненциального распределения используются также:
- распределение Вейбулла
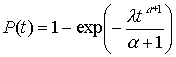 .
.
Экспоненциальное распределение
является частным случаем закона Вейбулла (при α = 0).
- распределение Эрланга
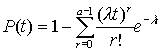 ,
,
где а - положительное целое
число.
Экспоненциальное распределение является частным случаем распределения Эрланга при а=1.
Зная изменения во времени вероятности успеваемости обработки 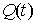 , можно определить математическое ожидание времени не успеваемости тем или иным контролируемым:
, можно определить математическое ожидание времени не успеваемости тем или иным контролируемым:
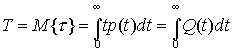 ,
,
где 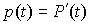 .
.
Аналогично определяется дисперсия времени не успеваемости:
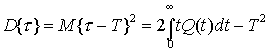 .
.
В случае экспоненциального
распределения получим следующие выражения для математического ожидания,
дисперсии времени не успеваемости и интенсивности не успеваемости:
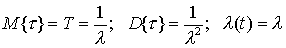 .
.
Рассмотрим модели восстановления
успеваемости.
1. Мгновенное восстановление успеваемости, когда временем обработки материала можно пренебречь по сравнению со временем не успеваемости.
Пусть после обработки
i-го материала в момент времени
t=0 контролируемый справляется с материалом. Но через время τ1 он не успевает. В этот момент мгновенно происходит отдых контролируемого. Однако через некоторое время τ2 контролируемый снова устаёт. Этот процесс может продолжаться многократно.Момент времени п-го усталости равняется:
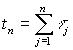 .
.
Если восстановление потенциала успеваемости происходит мгновенно, то моменты не успеваемостия или усталости t1, t2, ..., tn образовывают поток П1iобрабатываемогоi-го материала.
В общем случае интервалы времени
τj, j == 1,2,... являются случайными величинами, поэтому соответствующий поток также является
случайным. Случайные величины τj, j =1,2,... в общем случае можно охарактеризовать функцией
распределения в виде
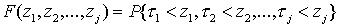 .
.
Поток обрабатываемого материала с функцией распределения
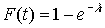
называется простейшим или стационарным пуассоновским потоком.
2. Восстановление успеваемости обработки с конечным временем восстановления, когда восстановление сил сопоставимо со временем неуспеваемости.
Процесс не успеваемости и восстановления с конечным временем восстановления успеваемости по ?-му материалу можно представить в виде чередующихся интервалов упеваемости или сохранение (состояние Е0 ) и восстановление успеваемости (состояние Е1). В момент времени 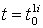 , соответственно требованию к объёму обрабатываемого материала. Для этого требуется время φ1.Потом начинается не успеваемость обработки материала. Продолжительность этого промежутка времени равняется τ1. Для повторного восстановления сил по обработке требуется время φ2. Моменты времени
, соответственно требованию к объёму обрабатываемого материала. Для этого требуется время φ1.Потом начинается не успеваемость обработки материала. Продолжительность этого промежутка времени равняется τ1. Для повторного восстановления сил по обработке требуется время φ2. Моменты времени
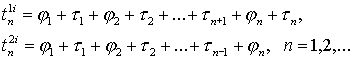
называются соответственно моментами не успеваемости и восстановления сил. Время восстановления сил меньше времени не успеваемости, но эта разность небольшая.
Если функция распределения времени восстановления сил равняется
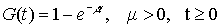 ,
,
то восстановление сил успеваемости называют экспоненциальным. При этом математическое ожидание и дисперсия времени восстановления сил определяются формулами:
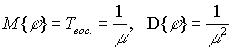 .
.
Особенность экспоненциального
восстановления сил состоит в том, что если в момент времениt контролируемый занят восстановлением сил, то распределение оставшегося времени восстановления будет экспоненциальным с тем же параметром m.
Пусть подготовленно контрольное количество из Nматериала. Для любого
контролируемого все материал делятся на две группы: материал, который обработан (1); материал, который не обработан (0).
Если число неправильных обработок по всему материалу составляет М, то их доля равняется
P = M / N.
Обычно число N довольно велико, поэтому целесообразно задавать не все N материал , а лишь выборку объема n. Пусть т - доля необработанного объёма материала, тогда оценка доли не успеваемости равняется
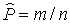
В этом случае для определения вероятности того, что при предложении п материала из N будет зафиксировано т не обработанного по условию их общего числа М, можно использовать классическую формулу отношения числа благоприятных исходов к общему числу результатов.
Если измерять правильность каждой обработки числом, то при предоставлении контролируемому п выборки объма материала, получим п чисел z1,z2,...,zn. Наиболее часто используются два значения правильности - 0 и 1. При этом для правильной обработки z = 1, а для неправильного - 0. Иногда ответы оцениваются с использованием k-значимой шкалы. Истинность ответа при этом является дискретной величиной, которая принимает значение 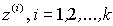 , причем z(k)и z(1) отвечают максимальному и минимальному количеству объёма материала.
, причем z(k)и z(1) отвечают максимальному и минимальному количеству объёма материала.
Если N >>1, п < 0.?N и Р =
М / N = соnst, то предельным распределением есть биномиальное распределение
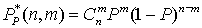 .
.
При пР = а и Р <0.1 предельным распределением является распределение Пуассона
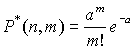 .
.
Зависимость вероятности
успеваемости от объёма материала называют характеристической кривой.
Уровень знаний может быть измерен, например, долей успеваемости обработки выборки.
Определим через 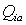 и Pia, и=1,2,...,пвероятности успеваемости и не успеваемости обработки материала и=1,2,...,п контролируемого со степенью подготовленности а. Вероятность Р*(п,т) того, что контролируемый при обработке п материала выборки не успеет обработатьт материал можно определить по формуле обобщенного биномиального распределения
и Pia, и=1,2,...,пвероятности успеваемости и не успеваемости обработки материала и=1,2,...,п контролируемого со степенью подготовленности а. Вероятность Р*(п,т) того, что контролируемый при обработке п материала выборки не успеет обработатьт материал можно определить по формуле обобщенного биномиального распределения
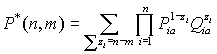
где zi. равняется 1 или 0 соответственно при успешной или не успешной обработки материала. Как допустимую аппроксимацию вместо вышеприведенной формулы целесообразно использовать биномиальное распределение
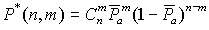
со средней вероятностью
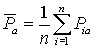 .
.
Эти соотношения применяются при
отсутствии времени между обработке материалов. При наличии таких связей вероятность Р*(п,т) может быть определена на основе использования цепей Маркова.
Обобщением при оценке объёма обрабатываемого материала с использованием k-значимой шкалы является распределение вида:
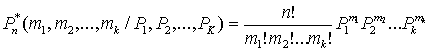 ,
,
где mi, и = 1,2,:,k-число обработанного материала z(и) на выборку с n материала;
Pi - доля материала со степенью успеваемости z(и) среди всего матеириала.
В конечном результате можно с определённой вероятностью сказать, что за тип приложения. Так как -1=<КУ=<+1, и имеются три типа приложений.
Математическая модель будет многокритериальной, так как будут использоваться критерии: социальные критерии (один из важнейших факторов), критерий время прибытия на рабочем месте (время провождения за определенным программным модулем), объём выполненной информации. В принципе критериев может быть гораздо больше. Всех их учесть это очень сложно. В конечном этапе математическая модель будет сводиться к однокритериальной - эффективность работы операторов. Так же к выше перечисленные математические методы можно добавлять другие математические методы в зависимости от реализации и конечного результата, а так же математическая модель будет комбинированной из имеющихся математических методов.
Эта входная информация обрабатывается несколькими математическими методами, которые описываются определённым шагам реализации обработки результатов. Если на данном этапе проектирования рассмотреть более детально, то это будет выглядеть так:
а) сбор входной информации, и её начальная обработка - использование симплекс метода для решения линейного программирования;
б) определение типов приложений по времени - использование системы с нечёткой логикой;
в) выдача конечного результата в виде диалогового сообщения и графиков - использование экспертной системы, поиск состояний в пространстве.
Математическая модель будет многокритериальной, так как используются критерии: социальные критерии (один из важнейших факторов), критерий время прибытия на рабочее место (время провождения за определенным программным модулем), критерий эффективности работы. В принципе критериев может быть гораздо больше. В конечном этапе математическая модель будет сводиться к однокритериальной. Так же к выше перечисленные математические методы можно добавлять другие математические методы в зависимости от реализации и конечного результата, а так же математическая модель будет комбинированной из имеющихся математических методов.
Информация может быть представлена в виде: графиков зависимости - время от типа приложения (необходимое, несущественное и не нужное приложения), время (период) от эффективности работы сотрудника; списки всех входных и выходных данных; диалоговое сообщение. Исходя из выше перечисленной информации, можно сделать вывод по выходной, конечной информации. Общая статистика по количеству проработанного времени, делится:
- на время, проведённое за необходимой работой (то есть время, для бухгалтеров приложения связанные с бухгалтерским учётом, и так далее);
- на время, проведённое за несущественным приложением (то есть, время, за которое операторов ЭВМ может проводить своё рабочее время, не отвлекаясь от основной работы);
- на время, проведённое за не нужным приложением (то есть, время, за которым операторов ЭВМ отвлекается от основной работы и которое влияет на работоспособность операторов ЭВМ);
- на время, проведенное за отдыхом (то есть, время, за которым операторов ЭВМ вообще не работает);
- общий объём выполненной работы операторов ЭВМ.
А так же дополнительная информация, например:
а) качество умения работы на компьютере;
б) качество надёжности работы компьютера.
Диалоговое сообщение подразумевает вывод сообщений в диалоговом окне по поводу ответа об анализе эффективности работы операторов ЭВМ. В данном случае компьютер ведёт общую статистику работы за всё время работы на данном предприятии, объём выполненной работы, и выдаёт сообщение исходя из статистики за прошедшее всё время. Это сообщение будет выдаваться с некоторой вероятностью, которая будет определяться исходя из статистики.
Принцип работы системы является закрытая система управления.
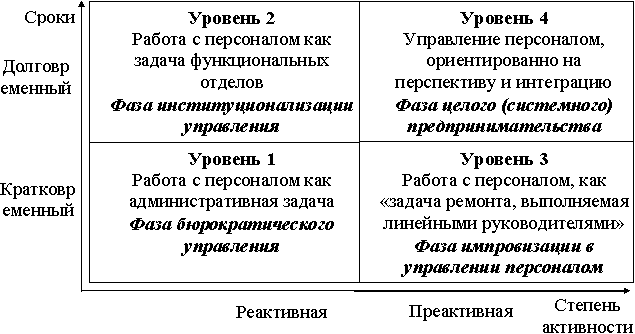
Рисунок 1. Принцип работы системы.
На рис 1 показаны блоками входные и выходные данные:
- входные данные, то есть период опроса системы, базовые знания о программах, а также об объёме выполняемой работы. Одним словом, все вводимые данные, например, системным администратором перед началом работы системы;
- влияющие факторы, то есть социальные факторы;
- сбор и обработка данных, то есть сбор данных с учётом входных данных, а затем обработка данных с учётом влияющих факторов и выходных данных;
- выходные данные, то есть все выходные данные системы, которые были перечислены выше.
Эти выходные данные влияют на будущие выходные данные, то есть учитываются при обработки новых данных и выходе новых выходных данных.
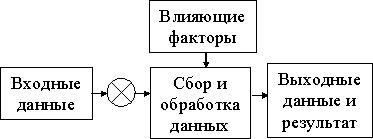
Рисунок 2. Уровни развития управления персоналом
Если расписать рис 2, то получится так [3]:
Уровень 1 ограничивается решением оперативных задач. Уровень 2 показывает, что ответственные за управление персоналом в соответствии с распоряжением администрации предприятия, но без привлечения линейных руководителей пытаются применить отдельные изолированные методы воздействия, рассчитанные на долгосрочную перспективу. Уровень 3 иллюстрирует, что линейные руководители в порядке профилактики берут кадровые вопросы в свои руки и самостоятельно, импровизируя, решают их как "ремонтные задачи на линии".
Уровень 4 объясняет, что ответственные за управление персоналом в качестве стратегических партнеров и членов руководящей команды предприятия совместно с линейными руководителями и при участии сотрудников предприятия развивают, реализуют и контролируют концепцию, ориентированную на достижение долгосрочных целей. Это содействует выполнению планов предприятия и интеграции важнейших функций управления персоналом.
При этом учитываются внутренние и внешние факторы функционирования фирмы. К первым обычно относят цели, стиль работы, характер решаемых задач, отношения между людьми в группах, стиль и опыт руководителя. Вторые факторы объединяют профсоюзы, правительственное регулирование и законодательство, экономические условия (в том числе конкуренция), структурный состав рабочей силы в стране, местоположение предприятия.
Таблица 1. Характеристика двух подходов к понятию персонала
| Персонал - издержки | Персонал - ресурс |
| Принуждение | Целесообразность |
| Минимизация | Оптимизация |
| Малый период планирования | Длительный период планирования |
| Результаты | Средства + Результаты |
| Количество | Качество |
| Негибкий | Гибкий |
| Зависимый | Автономный |
ЗАКЛЮЧЕНИЕ
В результате проектирования были получены следующие результаты: было выяснено то, что в настоящее время все существующие системы учёта работы операторов анализируют не качество и умение работы, а количество времени, проведенное на рабочем месте. Необходимо улучшать систему контроля и анализировать систему контроля. Затем можно будет внедрять во многие уже существующие системы контроля.
Следующим этапом в работе предполагается написание программы для более точного анализа процесса. Для этого необходимо более детальное изучение практической стороны анализа работы операторов ЭВМ. Следующим этапом предполагается выбрать систему, где можно будет внедрить и испробовать в настоящих условиях работы оператора.
ЛИТЕРАТУРА
- Маслов Владимир, О стратегическом управлении персоналом/ - "Проблемы управления и информатика", №5, 2002 год, страницы 99-105
- Журавская И. М., Некоторые аспекты совершенствования системы управления организацией/ - "Автоматизация и современные технологии", №4, 2002 год, страницы 30-33
- Аткинсон Р., Бауэр Г., Кротерс З. Введение в математическую теорию обучения: Пер. с англ. - М.: Мир, 1969. - 486 с.
- Свиридов А.П. Условные и безусловные алгоритмы диагностического контроля подготовки операторов ЭВМ. - М.: Моск. энерг. ин-т, 1987. -69с.
- Свиридов А.П. Применение методов планирования эксперимента при обучении обучающих и контролирующих машин. - М.: Моск. энерг. ин-т, 1975.-65с.
- Ржецкий Н.Н. Проверяющий стандартизированный контроль знаний и его зффективность. - К.: КИСИ, 1965. - 68 с.
- http://www.silur.comОфициальный сайт ОАО Силур города Харцызска


![]() ,
,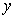 - успевемость, обусловленное числом правильных воспроизведений (успехов) за единицу времени;
- успевемость, обусловленное числом правильных воспроизведений (успехов) за единицу времени;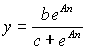
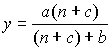 ,
,![]() ,
,![]() - константа.
- константа.![]()
![]() .
.![]() ,
,![]() .
.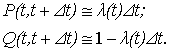
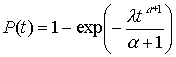 .
.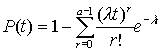 ,
,![]() , можно определить математическое ожидание времени не успеваемости тем или иным контролируемым:
, можно определить математическое ожидание времени не успеваемости тем или иным контролируемым: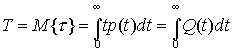 ,
,![]() .
.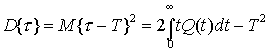 .
.![]() .
.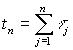 .
.![]() .
.![]()
![]() , соответственно требованию к объёму обрабатываемого материала. Для этого требуется время φ1.Потом начинается не успеваемость обработки материала. Продолжительность этого промежутка времени равняется τ1. Для повторного восстановления сил по обработке требуется время φ2. Моменты времени
, соответственно требованию к объёму обрабатываемого материала. Для этого требуется время φ1.Потом начинается не успеваемость обработки материала. Продолжительность этого промежутка времени равняется τ1. Для повторного восстановления сил по обработке требуется время φ2. Моменты времени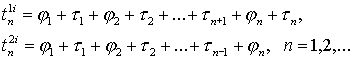
![]() ,
,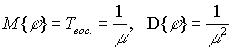 .
.![]()
![]() , причем z(k)и z(1) отвечают максимальному и минимальному количеству объёма материала.
, причем z(k)и z(1) отвечают максимальному и минимальному количеству объёма материала.![]() .
.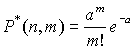 .
.![]() и Pia, и=1,2,...,пвероятности успеваемости и не успеваемости обработки материала и=1,2,...,п контролируемого со степенью подготовленности а. Вероятность Р*(п,т) того, что контролируемый при обработке п материала выборки не успеет обработатьт материал можно определить по формуле обобщенного биномиального распределения
и Pia, и=1,2,...,пвероятности успеваемости и не успеваемости обработки материала и=1,2,...,п контролируемого со степенью подготовленности а. Вероятность Р*(п,т) того, что контролируемый при обработке п материала выборки не успеет обработатьт материал можно определить по формуле обобщенного биномиального распределения 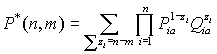
![]()
![]() .
.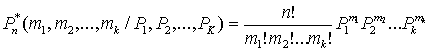 ,
,
