ГРАФИЧЕСКАЯ ИМИТАЦИЯ ФОРМИРОВАНИЯ МИКРОПРОФИЛЯ ПОВЕРХНОСТИ ПРИ ШЛИФОВАНИИ

Корниенко А.С., Гусев В.В. (каф. МСиИ, ДонНТУ, г. Донецк, Украина) ). - Инженер.Студенческий научно-технический журнал. - Донецк: ДонНТУ, 2003. №4. - с. 123 - 127.

Прогнозирование характеристик микропрофиля обрабатываемой поверхности является одной из наиболее важных посылок при оптимизации процессов шлифования. Если большинство показателей поверхностного слоя детали напрямую зависят от регламентированных показателей круга, таких как зернистость, концентрация зерен и т.д., то другие, такие как форма зерна, количество вершин зерен на единице площади, плотность распределения зерен по высоте и по площади рабочей поверхности, не определены и изменяются в процессе обработки. В настоящее время существуют экспериментальные и аналитические методы [1,2], которые описывают состояние рабочей поверхности обрабатываемой детали. Аналитический подход с использованием имитационных моделей является универсальным, но применение имитационных моделей связано с большими затратами времени.
В настоящей статье представлена имитационная модель, которая имеет простую структуру и предусматривает вывод графической информации на дисплей персонального компьютера. Моделируется процесс формирования микропрофиля при шлифовании. В основе моделирования положен принцип формирования микропрофиля поперечного сечения обрабатываемой поверхности посредством наложения поперечных сечений царапин, которые оставляют отдельные зерна шлифовального круга.


Рис.1. Схема формирования микропрофиля в поперечном сечении детали.

При построении модели пользуются следующими ограничениями:
-система станок-приспособление-инструмент-деталь является абсолютно жесткой;
-абразивный круг не имеет радиального биения;
-пластическое течение материала игнорируется;
-прочие физико-механические и физико-химические процессы в зоне резания не участвуют в образовании микропрофиля.

В образовании микропрофиля существенное значение оказывает структура поверхностного слоя абразивного слоя шлифовального круга.

При обработке учитывается, что не весь абразивный слой внедряется в обрабатываемый материал. Глубина части поверхностного слоя формирующей конечный микропрофиль детали, равна параметру Rmax

Для реализации описанного принципа моделирования производится построение плоскости произвольного поперечного сечения обрабатываемой детали. Здесь же вводится система координат zOt (рис. 1). Зерна из указанного слоя круга оставляют следы в прямоугольнике. Каждый след характеризуется своим профилем и положением, задаваемой через координаты его вершины.

Как было сказано ранее, распределение вершин зерен в рабочей поверхности круга не является равномерным. Исходное состояние и изменение разновысотности при обработке материалов адекватно описывается законом распределения Вейбулла-Гнеденко

,

где x0 и m – параметры закона распределения Вйбулла-Гнеденко для конкретной зернистости абразивного круга.

А при оценке числа зерен, находящихся на площади контакта необходимо исходить из закона Пуассона. В этом случае вероятность нахождения в единице объема m зерен имеет вид

где qV- параметр закона распределения Пуассона.

Параметр распределения Пуассона qVравен одновременно математическому ожиданию и дисперсии случайной величины. Для инструмента со статически равномерным распределением частиц в объеме справедливо выражение [3]

,

где qV – число абразивных частиц в единице объема, шт./мм3;

Кц – коэффициент концентрации, показывающий во сколько раз данная концентрация отлична от принятой за 100%;

– навеска абразива для получения в объеме концентрации, принятой за 100% или за единицу, г;

W – объем абразивного слоя, см3.

При рассмотрении формы поперечного среза зерна наиболее часто используют универсальное выражение, описывающее изменение ширины зерна от его высоты [4]

,

где С и m – эмпирические коэффициенты;

u – координата, отсчитываемая от вершины алмазного зерна.

При использовании нового абразивного круга значения коэффициентов С = 0,4, m = 0,65. А при использовании износившегося шлифовального круга С = 0,4 и m =0,5, при этих значениях коэффициентов изменение ширины зерна совпадает с идеальной формой эллипса.

Алгоритм расчетов по приведенным зависимостям представлен на блок-схеме (рис.2). Программа, реализующая алгоритм, написана при помощи САПР MathCAD.

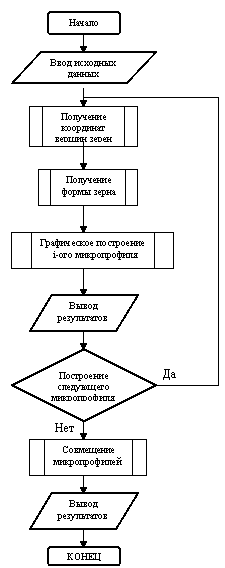
Рис.2. Алгоритм расчета и вывода графической информации.

При несоответствии вводимых исходных данных, с данными, представленными в программе, возможно их изменение. Совокупность изображений царапин дает изображение микропрофиля, копию которого можно просмотреть, а при необходимости вывести на печать.

В результате моделирования можно проследить изменение шероховатости в зависимости от состояния абразивного круга, исходя из того, что у нового и у износившегося круга форма зерна будет различной. Для нового круга изменение ширины зерна от высоты будет подчиняться закону

, а для износившегося круга справедлива следующая зависимость

.

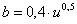Таким образом, можно наблюдать изменение шероховатости в зависимости от состояния шлифовального круга.

Рис.3. Микропрофили при обработке новым (b=0,65) и изношенным (b=0,5)

шлифовальными кругами.

После касания поверхности детали с шлифовальным кругом общий характер микрорельефа не изменяется, но положение рисок в продольном сечении уже не соответствует начальной шероховатости. Там, где был выступ, может появиться впадина, на месте бывшей впадины может появиться выступ.

Полученные данные показывают, что величина поперечного слоя единичного среза зависит не только от положения зерна на поверхности круга, его расстояния от центра, но и от его положения относительно единичных выступов и впадин шероховатости в продольном сечении.

Площадь срезаемого слоя металла максимальна при попадании вершины зерна на выступ шероховатости и минимальна при попадании во впадину шероховатости. Форма поперечного сечения срезаемого слоя также разнообразна, но наиболее характерна форма в своей нижней части, соответствующая профилю единичного зерна, а верхней части – профилю вершин нескольких (двух – трех) абразивных зерен.

Результаты моделирования параметров при шлифовании дали хорошее согласие с экспериментальными данными.