Корниенко А.С., Гусев В.В. (ДонНТУ, г. Донецк, Украина)
In this operation process of formation of a microrelief of a ceramics surface is modelled at a surface grinding. At a stage of simulation the opportunity of occurrence of a brittle failure on a surface of preparation also is taken into account.
Эксплуатационные характеристики деталей из технической керамики, наряду с условиями работы и параметрами, характеризующих состав, структуру и механические свойства взаимодействующих поверхностей определяются параметрами, характеризующими состояние поверхностного слоя деталей и зависящие от условий механической обработки заготовок. Из геометрических параметров наиболее изучено влияние на эксплуатационные показатели шероховатости поверхности, которая является простым и надежным критерием оценки состояния технологического процесса механической обработки и условий эксплуатации. Независимо от исходной шероховатости при работе в узлах трения происходит структурная приспосабливаемость материалов находящихся в контакте. Формируется выгоднейшее сочетание механических, физических, химических и геометрических факторов разделительного слоя, что характерно для данной пары и условий трения. Эксплуатационная шероховатость является оптимальной для данной пары трения. И.В. Крагельский и В.С. Комбалов [1] для шероховатости, сформировавшейся в процессе приработки, ввели понятие “равновесной шероховатости”, которая может быть как меньше, так и больше исходной. Микрорельеф поверхности керамики, который получают в результате механической обработки, оказываетвлияние на величину и интенсивность износа детали [2]. Поэтому для деталей, работающих в стационарных условиях, важным является уменьшение и сокращение времени их приработки. Необходимо при механической обработке обеспечить оптимальную структуру поверхностного слоя рабочих поверхностей деталей пары трения.
Аналитический подход с использованием имитационных моделей является универсальным, и позволяет визуально исследовать образование микрорельефа при шлифовании деталей, определить влияние на его формирование характеристик круга и параметров рабочей поверхности [3].
В основе имитационного моделирования формирования поверхностного слоя керамики при алмазном шлифовании положен принцип формирования микропрофиля поперечного сечения обрабатываемой поверхности посредством наложения поперечных сечений царапин, которые оставляют отдельные зерна шлифовального круга. Модель формирования микрорельефа поверхности керамики была разработана применительно к схеме плоского шлифования периферией круга.
Формирование поверхностного слоя на керамической заготовке происходит в результате удаления материала припуска при копировании формы зерна круга и скола группы зерен керамики в очаге разрушения. При хрупком разрушении в виде скола профиль канавки, оставленной зерном, не имеет сходства с профилем зерна, и параметры канавки превышают теоретическую глубину и ширину резания зерном. Разрушение керамики в виде очагов шириной является случайным процессом, зависящим от режимов резания. При построении модели пользуются следующими ограничениями:
- система станок-приспособление-инструмент-деталь является абсолютно жесткой;
- абразивный круг не имеет радиального биения;
- пластическое течение материала игнорируется;
- исходное состояние и изменение разновысотности зерен на рабочей поверхности круга описывается законом распределения Вейбулла-Гнеденко;
- при оценке числа зерен, находящихся на площади контакта, и определении расстояния между зернами исходили из закона Пуассона;
-форма поперечного среза зерна описывается параболической зависимостью;
- при хрупком разрушении материала в виде скола его ширина c определяется степенной зависимостью;
-распространение разрушения вглубь керамики при очаговой форме разрушения равно половине размера ширины скола 0,5b c;
- появление скола моделировалось случайной дискретной величиной распределенной по законам Пуассона, для этой цели был использован метод статистических испытаний (метод Монте-Карло).
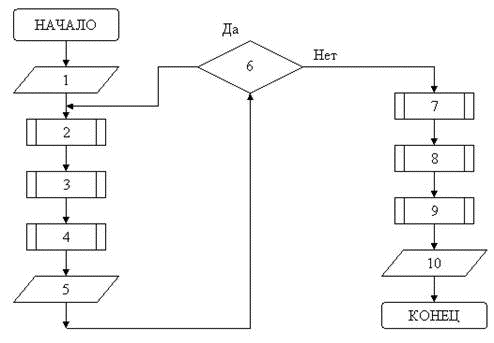
Алгоритм расчетов по приведенным зависимостям представлен на блок-схеме (рис.1). Программа, реализующая алгоритм, написана при помощи САПР MathCAD .
В процессе взаимодействия отдельных зерен круга с обрабатываемой поверхностью после первого прохода формируется начальный микропрофиль. После касания второго и последующих профилей начального не все зерна второго взаимодействуют с начальным профилем, т.е. некоторые зерна попадают в полости, полученные от зерен начального профиля, либо совсем не попадают в зону контакта с обрабатываемой поверхностью. Также при обработке наблюдается хрупкое разрушение обрабатываемого материала в виде сколов.

Рисунок 1 - Алгоритм построения микропрофиля.
1 - ввод исходных данных;
2 - получение координат вершин зерен в зависимости от их количества и плотности распределения;
3 - получение формы зерна зависящего от степени износа круга;
4 - графическое построение i-ого микропрофиля;
5 - вывод результатов;
6 - построение следующего микропрофиля;
7 - совмещение микропрофилей с заданным смещением Δ;
8 - расчет площади полученной в результате пересечения существующего и последующего профилей;
9 - построение окончательного профиля(1-го за вычетом всех i -х)
10 вывод результатов;
Удаляемый припуск разбивался на вертикальные слои, равностоящие друг от друга на величину Δ (до 1 мкм), и горизонтальные слои. Горизонтальные слои образованы пересечением вертикальных слоев с траекторией движения круга. После формирования профиля заготовки в начальном сечении, его перемещали на величину вертикального и горизонтального разбиения вплоть до окончательного формирования микрорельефа детали. На первом этапе формирование поверхности осуществлялось без учета хрупкого разрушения припуска сколом.
Величина единичного среза на зерне зависит не только от положения зерна на рабочей поверхности круга (его расстояния от центра), но и от его положения относительно единичных выступов и впадин шероховатости в продольном сечении. Площадь срезаемого слоя материала максимальна при попадании вершины зерна на выступ шероховатости и минимальна при попадании во впадину микрорельефа. Форма поперечного сечения срезаемого слоя разнообразна. В нижней части среза его форма соответствует профилю единичного зерна, а в верхней части – профилю вершин нескольких абразивных зерен.

Рисунок 2 – Схема взаимодействия отдельных зерен двух различных профилей.
На рисунке 2 показаны:
1)следы зерен начального профиля, вступившие в контакт с обрабатываемой поверхностью;
2)следы зерен начального профиля, не вступившие в контакт с обрабатываемой поверхностью;
3)следы зерен второго профиля, вступившие в контакт с первым профилем;
4)следы зерен второго профиля, не вступившие в контакт с первым профилем;
5)площадь, снимаемая зернами второго профиля;
6)поверхность скола.
На втором этапе моделирования учитывали возможность появления сколов на поверхности заготовки. Вероятность появления скола материала керамики при его срезании алмазным зерном определяется структурой материала и величиной параметров резания. Так как силы резания на одном зерне зависят от сечения среза материала на нем, то можно предположить, что и средняя ширина скола будет зависеть от площади сечения среза зерном f з . При линейной зависимости силы от сечения среза можно предположить, что элементарная случайная функция ширины скола также имеет линейную зависимость от сечения среза. При наличии скола определяются его размеры. Для моделирования случайной дискретной величины, каковой является число сколов, нами был использован метод статистических испытаний (метод Монте-Карло). В математической модели, разработанной в работе, появление скола моделировалось по закону Пуассона. Вероятность появления сколов определялась с помощью функции генерации случайных чисел по всем интервалам разбиения припуска, сумма которых составляет глубину резания.
Результаты моделирования параметров при шлифовании дали хорошее согласие с экспериментальными данными. Данная модель может быть использована для выбора характеристик шлифовального круга и прогнозирования параметров шероховатости поверхности керамических изделий при алмазном шлифовании.
Список литературы:
1. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. –М.: Машиностроение, 1977 – 526с.
2. Суслов А.Г. Качество поверхностного слоя деталей машин –М.: Машиностроение, 200 – 320с.
3. Новоселов Ю.К. Динамика формообразования поверхностей при абразивной обработке. – Саратов: Издательство Саратовского университета, 1979. – 232с.