Назад
К вопросуо силах, действующих на задней поверхности инструмента при резании
А.Б. Кравченко
Источник:
http://sstu.edu.ru/research/sstu_works/herald_techsc/10/17.doc
Рассматривается вопрос о влиянии напряженно-деформированного состояния, вызываемого силами, действующими на передней поверхности инструмента, на перемещения в зоне задней
поверхности.
Вопрос о силах, действующих на задней поверхности инструмента при резании имеет не только академическое, но и прикладное значение. Дело в том, что инструменты, как правило, изнашиваются по задним поверхностям, и этот процесс в основном связан с силовыми взаимодействиями между обрабатываемым изделием и задней поверхностью инструмента. Определение этих сил сопряжено с известными трудностями.
 Рисунок 1. Схема сил при свободном резании.
На рисунке 1 представлена схема сил, действующих в зоне резания. Силы PN и FN на передней поверхности и соответственно N и F3 на задней являются следствием внедрения резца под действием равнодействующей силы R. В силу вневершинного расположения силы возникает момент M.
На основании рис. 1. можно записать уравнения механики резания:
Рисунок 1. Схема сил при свободном резании.
На рисунке 1 представлена схема сил, действующих в зоне резания. Силы PN и FN на передней поверхности и соответственно N и F3 на задней являются следствием внедрения резца под действием равнодействующей силы R. В силу вневершинного расположения силы возникает момент M.
На основании рис. 1. можно записать уравнения механики резания: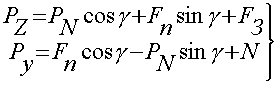 ; (1)
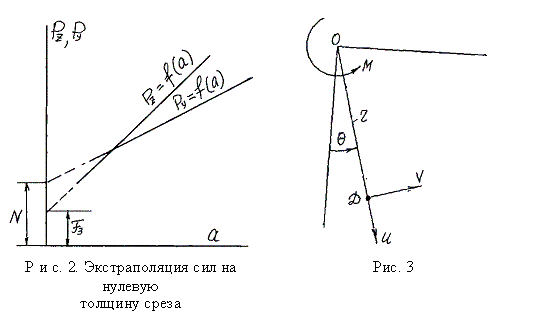
Два уравнения (1) имеют четыре неизвестные величины. Силы PZ и PY определяются динамометрированием. Методику определения сил F3 и N предложил проф. А.И. Розенберг [10]. Суть методики заключается в следующем. Производят резание с уменьшающейся толщиной среза a в условиях постоянной температуры, величина которой поддерживается соответствующим подбором скорости резания. При этом замеряются силы резания PZ и PY . Результаты наносятся в координатной системе PZ(PY) - a. В этих условиях зависимости PZ = f(a) и PY = f(a) имеют вид прямых линий. Отрезки, которые отсекаются на оси PZ(PY) с учетом масштаба, считаются искомыми силами N и F3 (рисунок.4). Этот метод в литературе называется «метод экстраполяции на нулевую толщину среза». В основе описанного метода лежат допущения, что толщина среза не влияет на силы, возникающие на задней поверхности инструмента, и силы на передней и задней поверхностях являются отдельными группами и не связаны между собой.
; (1)
Два уравнения (1) имеют четыре неизвестные величины. Силы PZ и PY определяются динамометрированием. Методику определения сил F3 и N предложил проф. А.И. Розенберг [10]. Суть методики заключается в следующем. Производят резание с уменьшающейся толщиной среза a в условиях постоянной температуры, величина которой поддерживается соответствующим подбором скорости резания. При этом замеряются силы резания PZ и PY . Результаты наносятся в координатной системе PZ(PY) - a. В этих условиях зависимости PZ = f(a) и PY = f(a) имеют вид прямых линий. Отрезки, которые отсекаются на оси PZ(PY) с учетом масштаба, считаются искомыми силами N и F3 (рисунок.4). Этот метод в литературе называется «метод экстраполяции на нулевую толщину среза». В основе описанного метода лежат допущения, что толщина среза не влияет на силы, возникающие на задней поверхности инструмента, и силы на передней и задней поверхностях являются отдельными группами и не связаны между собой.
 Силы, найденные с использованием указанной методики отличаются крайне небольшими значениями, на уровне 1,5-3 кг на погонный миллиметр режущей кромки. Возникает законный вопрос: за счет чего происходит износ инструментов, имеющих высокую твердость? Более того, известно, что с увеличением толщины среза износ интенсифицируется. Еще большее недоумение вызывает тезис о независимости сил на передней и задней поверхностях инструмента. Этот вопрос нами рассматривается ниже.
Пусть в точке O полубесконечной пластины приложен момент M (рис.3).
Положительное направление полярного угла θ принято в направлении против часовой стрелки. На этом же рисунке показаны положительные направления перемещений U и V. Напряжения, которые возникают в пластине от действия момента, описываются зависимостями [2], [3]:
Силы, найденные с использованием указанной методики отличаются крайне небольшими значениями, на уровне 1,5-3 кг на погонный миллиметр режущей кромки. Возникает законный вопрос: за счет чего происходит износ инструментов, имеющих высокую твердость? Более того, известно, что с увеличением толщины среза износ интенсифицируется. Еще большее недоумение вызывает тезис о независимости сил на передней и задней поверхностях инструмента. Этот вопрос нами рассматривается ниже.
Пусть в точке O полубесконечной пластины приложен момент M (рис.3).
Положительное направление полярного угла θ принято в направлении против часовой стрелки. На этом же рисунке показаны положительные направления перемещений U и V. Напряжения, которые возникают в пластине от действия момента, описываются зависимостями [2], [3]:
 ; (2)
Деформации определим на основании закона Гука:
; (2)
Деформации определим на основании закона Гука:
 ; (3)
где
; (3)
где 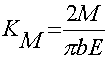 ; b - ширина пластины; m - коэффициент Пуассона; E - модуль упругости.
; b - ширина пластины; m - коэффициент Пуассона; E - модуль упругости.
Выражая деформации через перемещения, получим дифференциальные соотношения:
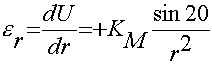 ; (4)
; (4)
 ; (5)
; (5)
 ; (6)
Перемещая и интегрируя выражение (4), найдем:
; (6)
Перемещая и интегрируя выражение (4), найдем:
 ; (7)
где f = (θ) является функцией одного только θ.
Подставляя (7) в (5) и интегрируя, получим выражение для определения V:
; (7)
где f = (θ) является функцией одного только θ.
Подставляя (7) в (5) и интегрируя, получим выражение для определения V:
 ; (8)
где f = (r) является функцией одного только r.
Далее, если (7) и (8) подставить в зависимость (6), то после преобразований найдем равенство:
; (8)
где f = (r) является функцией одного только r.
Далее, если (7) и (8) подставить в зависимость (6), то после преобразований найдем равенство:
 ; (9)
Это равенство должно удовлетворяться при любых значениях r и θ, поэтому каждая из двух независимых частей этого равенства должна быть равна нулю.
Рассмотрим левую часть равенства (9):
; (9)
Это равенство должно удовлетворяться при любых значениях r и θ, поэтому каждая из двух независимых частей этого равенства должна быть равна нулю.
Рассмотрим левую часть равенства (9):
 ; (10)
Решение уравнения (10) имеет вид:
; (10)
Решение уравнения (10) имеет вид:
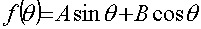 ; (11)
Аналогично для правой части равенства (9):
; (11)
Аналогично для правой части равенства (9):
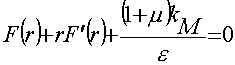 и соответственно:
и соответственно:
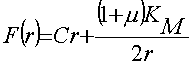 ; (12)
Подставляя (11) в (7) и (11), (12) в (8) будем иметь:
; (12)
Подставляя (11) в (7) и (11), (12) в (8) будем иметь:
 ; (13)
; (13)
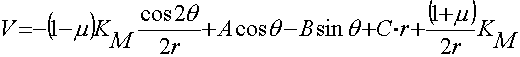 ; (14)
Исключая перемещения пластины как твердого тела, следует положить A = B = C = 0.
Таким образом, зависимости для перемещений приводятся к виду:
; (14)
Исключая перемещения пластины как твердого тела, следует положить A = B = C = 0.
Таким образом, зависимости для перемещений приводятся к виду:
 ; (15)
; (15)
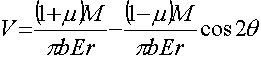 ; (16)
В конечном итоге нас интересуют перемещения части материала в левой и правой частях пластины (y<0 и y>0).
Очевидно, что при:
; (16)
В конечном итоге нас интересуют перемещения части материала в левой и правой частях пластины (y<0 и y>0).
Очевидно, что при:
θ = 0, U =0,
 ; (17)
; (17)
θ = ±p/2, U =0,
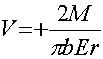 ; (18)
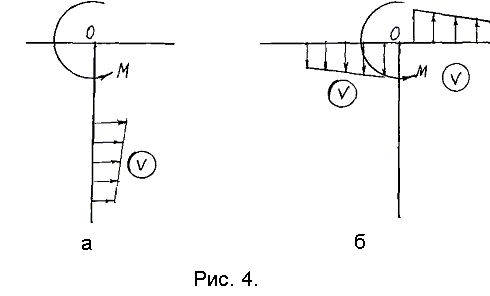
Перемещения, которые вытекают из зависимостей (17) и (18), графически могут быть интерпретированы как это показано на
рис. 4, а, б.
Если обратиться к рассмотрению рис.1 с учетом формул (17), (18) и построения на рис.4,б, можно утверждать, что под задней поверхностью резца за счет сил, действующих на передней поверхности (момент М), обработанная поверхность детали будет стремиться к «выпучиванию» (см. рис.4,б), т.е. возникает упругое взаимодействие между этой поверхностью и площадкой износа резца по задней поверхности. С увеличением параметров процесса резания растет момент резания, что сопровождается повышением напряженного состояния в районе задней поверхности инструмента. Более того, силы, возникающие в районе площадки износа резца, могут достичь значительных величин. Последнее подтверждается прямыми исследованиями с помощью метода разрезного резца [4], а также и подсчетами, приведенными в работе [5]. В работе [5] установлено, что, например, при резании стали ШХ15 в состоянии поставки резцом Т15К6, g = 0, a = 10; v = 100 м/мин при толщине среза a =0,25 мм (резание свободное) и износе резца w = 0,05 мм, сила N достигает значения P = 200 H на погонный миллиметр режущей кромки, что приводит к возникновению напряжений, равных sN = 400 МПа. Уместно заметить, что резание с толщиной a = 0,5 мм дает соответственно P = 300 Н и N = 600 МПа. Такой уровень напряжений достаточен для интенсификации износа.
; (18)
Перемещения, которые вытекают из зависимостей (17) и (18), графически могут быть интерпретированы как это показано на
рис. 4, а, б.
Если обратиться к рассмотрению рис.1 с учетом формул (17), (18) и построения на рис.4,б, можно утверждать, что под задней поверхностью резца за счет сил, действующих на передней поверхности (момент М), обработанная поверхность детали будет стремиться к «выпучиванию» (см. рис.4,б), т.е. возникает упругое взаимодействие между этой поверхностью и площадкой износа резца по задней поверхности. С увеличением параметров процесса резания растет момент резания, что сопровождается повышением напряженного состояния в районе задней поверхности инструмента. Более того, силы, возникающие в районе площадки износа резца, могут достичь значительных величин. Последнее подтверждается прямыми исследованиями с помощью метода разрезного резца [4], а также и подсчетами, приведенными в работе [5]. В работе [5] установлено, что, например, при резании стали ШХ15 в состоянии поставки резцом Т15К6, g = 0, a = 10; v = 100 м/мин при толщине среза a =0,25 мм (резание свободное) и износе резца w = 0,05 мм, сила N достигает значения P = 200 H на погонный миллиметр режущей кромки, что приводит к возникновению напряжений, равных sN = 400 МПа. Уместно заметить, что резание с толщиной a = 0,5 мм дает соответственно P = 300 Н и N = 600 МПа. Такой уровень напряжений достаточен для интенсификации износа.
 Таким образом, путем решения упругой задачи получены зависимости, на базе которых можно сделать заключение, что силы, возникающие на задней поверхности инструмента при резании, функционально связаны с напряженным состоянием на передней поверхности и зависят от режимов обработки.
Таким образом, путем решения упругой задачи получены зависимости, на базе которых можно сделать заключение, что силы, возникающие на задней поверхности инструмента при резании, функционально связаны с напряженным состоянием на передней поверхности и зависят от режимов обработки.
Перечень ссылок
- Розенберг А.М., Еремин А.Н. Элементы теории процессов резания металлов. М.: Машгаз, 1956, 320 с.
- Фрохт М.М. Фотоупругость. Том 2. Из-во Техн.-теорет. лит.. М., 1950. 488 с.
- Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1975. 575 с.
- Гордон М.Б.. Трение, смазка и износ инструмента при резании металлов. Чебоксары, 1978. 125 с.
- Кравченко А.Б. Обоснование заданных эксплуатационных характеристик деталей ГТД путем целенаправленного регулирования остаточных напряжений при лезвийной обработке: Дис. канд. техн. наук. Куйбышев, 1990.
Назад

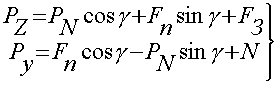 ; (1)
; (1)
 ; (2)
; (2) ; (3)
; (3)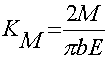 ; b - ширина пластины; m - коэффициент Пуассона; E - модуль упругости.
; b - ширина пластины; m - коэффициент Пуассона; E - модуль упругости.
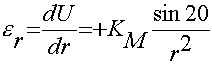 ; (4)
; (4) ; (5)
; (5) ; (6)
; (6) ; (7)
; (7) ; (8)
; (8) ; (9)
; (9) ; (10)
; (10)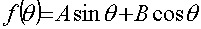 ; (11)
; (11)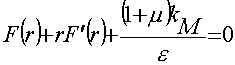
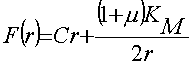 ; (12)
; (12) ; (13)
; (13)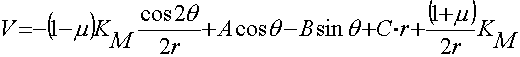 ; (14)
; (14) ; (15)
; (15)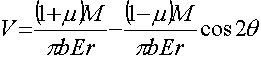 ; (16)
; (16) ; (17)
; (17)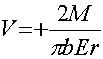 ; (18)
; (18)