Назад

Механика формирования обработанной поверхности при развертывании отверстий

Г.С .Железнов, Р.И. Бляхман, С.П. Петрова, В.А. Петров

Источник:

http://sstu.edu.ru/research/sstu_works/herald_techsc/10/16.doc

На основе анализа траектории движения оси развёртки и упругих деформаций обрабатываемой заготовки под действием сил резания определена механика формирования обработанной поверхности, предлагаются зависимости для оптимизации параметров процесса развёртывания по критерию точности обработки.
По способу формирования обработанной поверхности методы обработки точных отверстий в машиностроении можно разделить на две группы.

Первая группа – развёртывание и протягивание – основана на том, что заданного размера цилиндрическая инструментальная поверхность режущего инструмента копируется на обработанной заготовке – размер инструментальной поверхности с некоторыми отклонениями переносится на обработанную поверхность отверстия.

Вторая группа – шлифование и растачивание – характеризуется тем, что обработанная поверхность не является копией инструментальной поверхности, что позволяет одним инструментом обрабатывать поверхности с различными размерами в определённом интервале. Первая группа обеспечивает более высокую размерную стабильность и производительность, но менее универсальна, чем вторая. Однако технологические возможности первой группы по обеспечению точности и шероховатости обработанной поверхности более ограничены, чем второй, которая в принципе таких ограничений не имеет.

В серийном и массовом машиностроительных производствах при обработке отверстий не ниже шестого квалитета приоритет в применении имеет первая группа, в иных условиях – вторая группа.

Для обеспечения необходимой точности процессы второй группы требуют периодической многократной настройки режущего инструмента на заданный размер за период его стойкости, что обеспечивает, с одной стороны, возможность достижения высокой точности обработанной поверхности, а с другой – низкую производительность и большой расход режущего инструмента. При относительно малых диаметрах обрабатываемых отверстий (d < 20 мм) процессы второй группы не эффективны и даже не применимы. Поэтому наибольшее применение в машиностроении получило развёртывание как наиболее универсальный и более экономичный метод по сравнению с протягиванием. Однако в связи с тем, что инструментальная поверхность развёртки копируется на обрабатываемой заготовке с некоторыми отклонениями, зависящими от множества факторов, предсказать в процессе технологической подготовки производства параметры режущего инструмента и технологического процесса, обеспечивающие заданную точность, весьма затруднительно. Поэтому на практике технологу нередко приходится производить отработку процесса развёртывания с целью определения размеров, геометрических параметров развёрток и режимов развёртывания, что является существенным недостатком этого процесса. Он обусловлен тем, что пока не установлены количественные связи возникающих при обработке отклонений с факторами процесса развёртывания: размером и геометрическими параметрами режущего инструмента, режимами резания, свойствами обрабатываемого материала, размерами и формой обрабатываемых заготовок в местах расположения обрабатываемых отверстий.

Размеры обработанных развёрткой отверстий могут быть как больше, так и меньше её диаметра. В первом случае имеет место разбивка, а во втором – усадка. Для обеспечения требуемой точности обработки отверстий необходимо знать количественную связь этих величин с факторами процесса развёртывания.

Отклонение диаметра отверстия от диаметра развёртки определяется разбивкой P и усадкой U:

E = P - U. (1)

В связи с тем, что разбивка и усадка имеют разную физическую природу, установление вышеупомянутой количественной связи этих величин с факторами процесса развёртывания складывается из решения двух задач, относящихся к разбивке и усадке.

Нахождение математической зависимости разбивки от факторов процесса развёртывания эмпирическим путем не имело положительного результата [1, 2]: полученные разными исследователями зависимости противоречивы и имеют частный характер. Это объясняется множеством случайных факторов, действующих при развёртывании, и трудностями их исключения при проведении экспериментов. Приоритет имеют математические зависимости разбивки от факторов процесса развёртывания, полученные на основе анализа механизма её образования.

В общем случае разбивка может быть представлена суммой

P = Dти - D тз+ Dн + Dз + D у (2)

где слагаемые определяют составляющие разбивки, вызванные: Dти - нагревом развёртки при обработке; Dтз - нагревом обрабатываемой заготовки; Dн - образованием нароста; Dз - погрешностями заточки режущей части зубьев развёртки и их неодинаковым износом; Dу - несовпадением оси развертки с осью вращения шпинделя станка, обусловленным биением шпинделя станка и погрешностью установки инструмента на станке.

Однако из вышеуказанных составляющих разбивки существенное значение имеют лишь две (Dз и Dу), что объясняется следующим.

В связи с кратковременным характером процесса развёртывания и применением охлаждающих сред тепловые явления не оказывают существенного влияния на разбивку и поэтому можно принять Dти = 0 и Dтз = 0.

Развёртывание производится при таких скоростях резания, когда нарост не образуется, поэтому Dн = 0.

Таким образом, в основу математической модели разбивки могут быть положены две составляющие:

На рис. 1 показано положение оси развёртки О¢ Ои относительно оси вращения О¢ О в стационарном режиме обработки. Возникновение разбивки определяется тем, что при обработке ось развёртки не совпадает с осью её вращения и в поперечном сечении А–А, проходящем через точку пересечения режущего и калибрующего участков зубьев, смещена от оси вращения на расстояние ООи.

Рисунок 1. Отклонение оси развёртки от оси её вращения при обработке

Вышеуказанное смещение оси развёртки от оси вращения может быть вызвано двумя причинами.

Первая заключается в том, что ось развёртки перед обработкой не совпадает с осью вращения на величину О1О (рис. 2.) из-за биения шпинделя станка и ее неточной установки.

Это порождает при обработке боковую силу, вызывающую в переходном периоде обработки перемещение оси развёртки из точки О1 в точку Ои за счет изгиба ее стержня и податливости станка. В этом положении равнодействующая сил резания и сила реакции уравновешены. Наиболее удаленная от оси вращения точка режущей кромки зуба 1 (рис.2) вращается по окружности наибольшего радиуса и формирует обработанную поверхность отверстия, диаметр которого превышает диаметр развёртки на величину разбивки. Зависимость для расчета разбивки получили из уравнений равновесия сил, действующих на развёртку в стационарном режиме обработки и представляющих с учетом малости суммы проекции поперечных сил на координатные оси ОиХ и Ои У (рис.2).

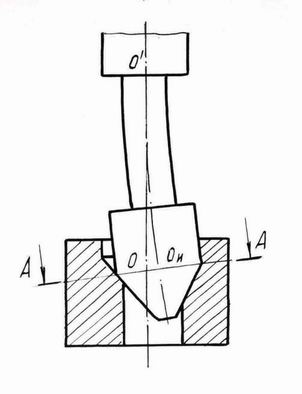
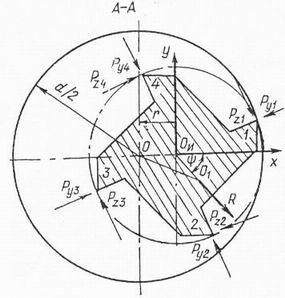
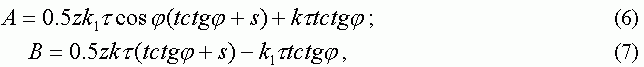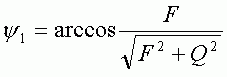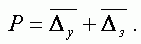Составив уравнения равновесия поперечных сил, действующих на развертку, в которых составляющие силы резания PZi и Pyi (рис.2) были выражены через фактическую глубину резания и подачу с учетом разбивки, а сила реакции R=GO1Ou - через прогиб стержня развертки и упругое перемещение шпинделя станка в сечении А-А, и решив их относительно разбивки, получили следующую зависимость для ее расчета

где G – жесткость крепления инструмента, определяемая жёсткостью стержня развёртки Gи и жёсткостью шпинделя станка GC,

Dи = ОО1 - смещение оси инструмента относительно оси вращения до обработки;

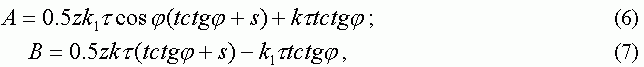
где z - число зубьев инструмента; t - касательное напряжение в плоскости сдвига, определяемое временным сопротивлением обрабатываемого материала s в и относительным удлинением d:t = 0,7sв (1+d); t и s - соответственно номинальные значения глубины резания и подачи на зуб; j - угол в плане; k, k1 - безразмерные коэффициенты, применительно к развёртыванию их можно принять k = k1 » 4.

При z = 2, m = cosy, при z = 4, m = siny.

При z> 4, m =1, y = arctg A/B.

Рисунок. 2 Схема формирования обработанной поверхности развёрткой, ось которой до обработки смещена от оси вращения

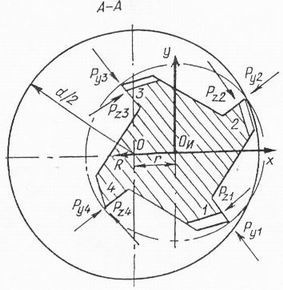
Рисунок. 3 Схема формирования поверхности при обработке развёрткой, имеющей биение режущих кромок
Составляющая Dy имеет решающее значение при развёртывании на станках невысокой точности. Расчеты показывают, что увеличение подачи, глубины резания, прочности обрабатываемого материала и уменьшение угла в плане, жесткости технологической системы также приводит к уменьшению разбивки. Применение для установки развёрток на шпинделе станка плавающих патронов позволяет устранить разбивку при углах в плане, не превышающих j = 15º, так как при больших углах в плане развёртка при обработке под действием осевой силы теряет продольную устойчивость. По этой же причине отклонение оси развёртки от оси обрабатываемого отверстия должно быть наименьшим.

Второй причиной образования разбивки является погрешность заточки режущей части развёртки, выражающейся биением режущих кромок, и неодинаковый износ зубьев. Биение режущих кромок определяется как разность наибольшего и наименьшего расстояний режущих кромок в рассматриваемом поперечном сечении от оси развёртки - d1. При этом имеет значение разность расстояний для двух соседних зубьев - D. Расстояние от режущей кромки до оси развертки для i - го зуба определяется

ri = r1+f(i), (8)

где r1 - расстояние режущей кромки первого в порядке заточки зуба до оси развертки; f(i) - функция распределения приращения по режущим кромкам, имеющая случайный характер.

Наиболее вероятным является распределение, когда каждый следующий в порядке заточки зуб выступает над предыдущим на величину D. Биение режущей части при этом составляет

d 1 = D (z-1). (9)

При обработке вследствие биения зубья развертки, точно установленной на станке, имеют неодинаковую нагрузку, порождающую боковую силу. Последняя вызывает перемещение развертки в сторону зубьев, характеризующихся меньшими расстояниями до оси вращения. При этом глубина резания и подача для зубьев с меньшими расстояниями увеличиваются , а для зубьев с большими расстояниями – уменьшаются. Зуб 2 (рис.3) вращается по окружности наибольшего радиуса и формирует обработанную поверхность отверстия диаметром d + Dp.

Из уравнений равновесия поперечных сил, в которых составляющие сил резания Pzi и Pyi (рис.3) были выражены через фактические значения подачи на зуб и глубину резания с учетом биения зубьев и разбивки, получили следующую зависимость для расчета последней:

При z = 2, n = cosy, при z = 4, n = siny1.

При z > 4, n = 1,

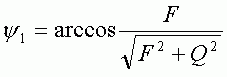
Полученные зависимости позволяют вычислять на ЭВМ разбивку при различных факторах процесса развёртывания и обеспечивать ее в заданных пределах. Расчеты показывают, что при значениях жесткости, характерных для реальных технологических систем, величина разбивки, вызванной биением режущих кромок, близка к величине этого биения. С увеличением глубины резания, подачи, с уменьшением угла в плане и жесткости технологической системы разбивка увеличивается.

Одинаковый износ режущих зубьев развёртки уменьшает разбивку, а неодинаковый износ может как уменьшать, так и увеличивать разбивку в зависимости от характера распределения износа по режущим зубьям развёртки. С целью обеспечения равномерного износа зубьев развёрток необходимо для их изготовления применять инструментальные стали с карбидной неоднородностью не выше второго балла.

В общем случае, когда обе причины являются существенными, разбивка определяется векторной суммой

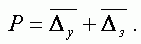
Верхней ее оценкой является сумма Pmax = Dз + Dy, нижней разность Pmin = |Dз - D y|, наиболее вероятной P = 0.5(D з + Dy).

Развёртывание отверстий сопровождается упругой деформацией заготовок, возникающей под действием силы резания. Исчезновение их после обработки приводит к усадке, т. е. восстановлению недеформированного состояния, которое приводит к образованию отклонений размера и формы обработанной поверхности. При обработке осесимметричных деталей изменение усадки вдоль оси отверстия приводит к образованию отклонений диаметра и профиля продольного сечения. При обработке деталей, не обладающих осевой симметрией в месте расположения отверстия, кроме вышеуказанных, образуются отклонения от круглости .

При проектировании технологических процессов и режущих инструментов для обработки отверстий в тонкостенных деталях по 6…8 квалитетам упругие деформации необходимо учитывать.

Аналитическое определение упругих деформаций в деталях с отверстиями представляет сложную проблему механики деформируемого тела. Известные аналитические решения [3,4] затруднительно использовать для прогнозирования усадки, так как они относятся к деталям простейшей формы: цилиндрам, кольцам и т.п.

Отсутствие необходимых расчетных зависимостей создает значительные трудности при подготовке производства: настроечные и исполнительные размеры развёрток, а также режимы резания при обработке отверстий в тонкостенных деталях приходится на практике отрабатывать на рабочих местах применительно к конкретным деталям и условиям их обработки.

С целью построения зависимости усадки от факторов процесса развёртывания провели исследование упругих деформаций наиболее распространенных деталей (рис.4…7) методом конечных элементов (МКЭ). Подробно изучали деформации деталей в постановке плоской задачи теории упругости. В качестве примера показана конечно-элементная модель (КЭМ) (рис.8) проушины и ее форма после развёртывания. На ЭВМ вычисляли радиальные перемещения шести точек, равномерно расположенных по периметру отверстия, при различных значениях основных факторов, к которым относятся : коэффициент тонкостенности K = r/R, изменяющийся в интервале 0,5...0,9; центральный угол a, соответствующий половине дуги наружной поверхности детали, очерченной по окружности радиусом R, принятой a = 0.1 рад. для полосы (рис.4), a = 0.1 рад. для проушины (рис.5), a = 2.3 рад. для корпуса подшипника (рис.6); число зубьев инструмента z, принимавшее значения 3,4,6. При каждом числе зубьев расчет проводился для различных взаимных положений инструмента и детали, имитирующих вращение инструмента.

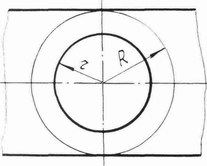
Рисунок. 4. Полос

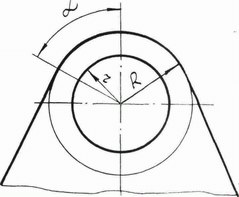
Рисунок. 5. Проушина

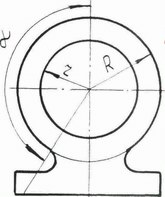
Рисунок. 6. Корпус подшипника

Рисунок. 7. Втулка

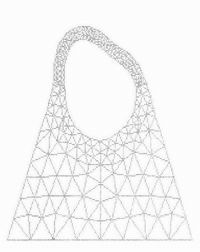
Рисунок. 8. Форма отверстия конечно-элементной модели после обработки трёхзубой развёрткой при К=0.8

В процессе развёртывания при отсутствии разбивки взаимодействие инструмента и детали в радиальном направлении является прессовым. Обратимое перемещение любой точки после обработки, т.е. упругая отдача, равно по модулю и противоположно по знаку тому перемещению, которое оно будет иметь при нагружении детали силами резания. По упругой отдаче расчетных точек определены усадка и отклонения от круглости отверстия. Зависимость этих величин от основных факторов аппроксимированы усредненными эмпирическими формулами степенного вида, параметры которых подобраны по методу наименьших квадратов.

С целью применения полученных результатов исследования деформации в постановке плоской задачи теории упругости для оценки деформаций реальных тел ставилась объемная задача и исследовалась закономерность изменения радиальных перемещений точек образующей поверхности отверстия детали - втулки. В результате этого исследования построили зависимости для определения поправочных коэффициентов к формулам, полученным в постановке плоской задачи. Вычисления проводили для того же диапазона значений коэффициента K, как и в плоской задаче, и различных отношениях K1 = H/r длины втулки H к радиусу r. Поправочные коэффициенты аппроксимированы зависимостями экспоненциального вида, позволяющими перейти от идеализированной плоской схемы к реальной объемной задаче.

Так как точные решения подобных задач не известны, то с целью верификации КЭМ проведен физический эксперимент на модели в виде детали - проушины из алюминиевого сплава Д16Т при R = 50 мм, K = 0.8, K1 = 0.48, a = p/2. Нагружение осуществляли специально разработанным устройством, измерение диаметра отверстия производили с применением тензорезистивных методов. Расхождение расчетных и экспериментальных результатов не превышало 5%.

Упругие деформации стенок заготовок в месте расположения обрабатываемого отверстия, возникающие под действием сил резания, в зависимости от формы и размеров обрабатываемой заготовки изменяются как по периметру окружности обрабатываемого отверстия, так и вдоль его оси. Изменение усадки по периметру приводит к образованию отклонения от круглости ЕFK, а изменение усадки по длине отверстия – к образованию отклонения профиля продольного сечения – EFP.

Усадку определяли как разность между действительным размером развёртки d2 и наименьшим диаметром обработанного отверстия dmin: EU = d2-dmin; отклонение от круглости определяли как разность между наибольшим и наименьшим диаметрами отверстия в том поперечном сечении, в котором она имеет наибольшее значение EFK = dmax-dmin, отклонение профиля продольного сечения - как разность наибольшего и наименьшего диаметров среднего и торцевого сечений в том продольном сечении, в котором она максимальна.

Обработав результаты вычислений упругих перемещений точек обрабатываемой поверхности, происходящих под действием сил резания, сопровождающих обработку, получили следующие зависимости при расчёте

В связи с тем, что упругие перемещения в торцовом сечении всегда больше, чем в среднем сечении обрабатываемого отверстия, то в зависимости от размера обратной конусности калибрующей части развёртки профиль продольного сечения будет иметь бочкообразность, если EFP, вычисленное по зависимости (24) меньше обратной конусности развёртки, иначе обработанное отверстие будет иметь конусообразность с меньшим диаметром обработанного отверстия в конце обработки.

Расчёты показывают, что упругие перемещения имеют существенное значение при обработке заготовок с коэффициентом тонкостенности K ³ 0.75. Поэтому при обработке заготовок, характеризующихся K < 0.75, следует ожидать образование разбивки. При K ³ 0.75 отклонения размеров обработанного отверстия от размера развёртки определяются разностью Er = P-U по приведённым выше зависимостям.

Приведённые здесь зависимости могут быть рекомендованы для оптимизации режимов резания и определения исполнительных размеров развёрток для обработки отверстий в заготовках различных форм и размеров.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

  1. Резников А.Н. Исследование разбивки отверстий при развёртывании // Станки и инструменты.1948. № 4. С.11…14.
  2. Солонин И.С. Статистические исследования точности и чистоты обработанной поверхности при развёртывании чугуна и стали // Тр. Урал. политехн. ин-та им. С.М.Кирова.. Сб.50. Свердловск: УПИ, 1956.
  3. Прочность, устойчивость и колебания: Справочник в 3-х Т.,Т.2/ Под ред. И.А.Биргера и Я.Г. Пановко.М.: Машиностроение,1968. 465 с.
  4. Колтунов М.А., Васильев Ю.Н., Черных В.А. Упругость и прочность цилиндрических тел. М.: Высш. школа, 1975. 526 с.
  5. Резание металлов и инструмент/ Под ред. А.М. Розенберга. М.: Машиностроение, 1964. 226 с.

Назад