УДК 658.382.3
О ПОЖАРНОЙ ОПАСНОСТИ СЕТЕЙ НАПРЯЖЕНИЕМ 380/220 В ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ И ЖИЛЫХ ЗДАНИЙ
Шевченко О.А.
Сборник научных трудов ДонНТУ. Серия: "электротехника и энергетика", выпуск 28: Донецк: ДонНТУ, 2001. - с. 182-185.
В сетях напряжением до 1000 В промышленных предприятий величина токов КЗ значительна. Например, ток при трехфазном КЗ на шинах подстанции (380/220 В) составляет 25-40 кА, на шинах главных цеховых силовых шкафов - 10-20 кА, а на зажимах электродвигателей (4-8 кВт) - 2 кА.
Резкое возрастание токов в короткозамкнутой цепи может вызвать: опасный нагрев токоведущих частей и воспламенение горючих изоляционных материалов в конструкции кабеля или оплетки провода, воспламенение пожароопасной и взрывоопасной среды при разбрызгивании расплавленного металла, из которого изготовляется проводник, сваривание электрических контактов, вызвать электрические дуги, обладающие воспламеняющей способностью и т. д, [1].
Анализ
данных УГПО УМВД Донецкой области за период с 1995 по
Следовательно, будем предполагать, что пожар в сети происходит при совпадении в пространстве и времени следующих случайных событий: КЗ в защищаемой сети; отказ в срабатывании (без выдержки времени) ближайшего к месту КЗ защитного коммутационного аппарата.
Задача данной работы состоит в следующем: определить вероятность безопасной работы рассматриваемого участка сети R(t), вероятность пожара в элементе сети Q(t), среднее время до первого пожара τ1 при условии, что в начальный момент времени в защищаемой сети не наблюдаются токи КЗ и система отключения и защиты коммутационного аппарата находятся в исправном состоянии.
Пусть изменения состояния рассматриваемого участка сети представим в виде марковского случайного процесса [2] ξ(t), с параметрами λ1 и μ1, который может принимать два значения: 0 - безопасное состояние (интервалы времени между появлениями КЗ в защищаемой сети) и 1 - опасное состояние (в сети произошло КЗ, длительность которого равна времени срабатывания защитного коммутационного аппарата). Аналогичной функцией η(t) с параметрами λ2 и μ2 описывается состояние защитного коммутационного аппарата: 0 - система защитного отключения коммутационного аппарата находится в исправном состоянии; 1 - система защитного отключения находится в отказавшем состоянии.
Рассмотрим случай, когда система защитного отключения без самоконтроля, т. е. при отказе защиты она не дает сигнал на отключение защитного коммутационного аппарата. Состояние защиты в течение рассматриваемого интервала времени t не проверяют. В этом случае принимаем μ2 = 0. К таким защитам, у которых μ2 = 0 можно отнести автоматические выключатели (пробки) жилых квартир.
Пожар от КЗ в защищаемой сети наступает в момент, когда ξ(t) = 1 и η(t)=1.
Совокупность процессов ξ(t) и η(t) рассмотрим как процесс Маркова с четырьмя дискретными состояниями и непрерывным временем.
Выразим вероятности Pi(t), i=0,3 нахождения системы в каждом из четырех возможных состояний через параметры известных процессов: λ1, μ1 и λ2. Поведение во времени такой системы полностью описывается системой линейных дифференциальных уравнений.
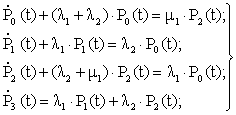 (1)
(1)
Система дифференциальных
уравнений (1) должна быть решена при следующих начальных условиях: ![]() ,
т.е. в начальный момент времени КЗ в защищаемой сети нет и система отключения
автоматического выключателя исправна и готова к работе в случае появления КЗ.
,
т.е. в начальный момент времени КЗ в защищаемой сети нет и система отключения
автоматического выключателя исправна и готова к работе в случае появления КЗ.
Используя преобразование Лапласа [3] систему линейных дифференциальных уравнений (1) приведем к системе алгебраических уравнений вида
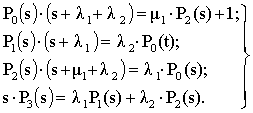 (2)
(2)
Решая систему
алгебраических уравнений (2) относительно![]() ,
, ![]() находим:
находим:
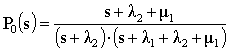 ;
(3)
;
(3)
![]() ;
(4)
;
(4)
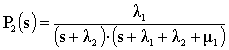 (5)
(5)
![]() .
(6)
.
(6)
Переходим в формулах (3), (4), (5) и (6) от изображения к оригиналам, получим:
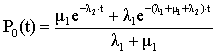 ;
(7)
;
(7)
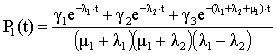 ,
(8)
,
(8)
где
![]() ;
(9)
;
(9)
![]() ;
(10)
;
(10)
![]() ;
(11)
;
(11)
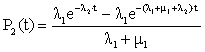 (12)
(12)
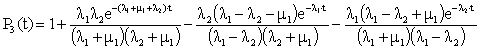 .
(13)
.
(13)
Вероятность безопасной
работы в течение времени t определяется суммой
вероятностей ![]() ,
, ![]() и
и ![]() ,
т. е.
,
т. е.
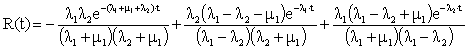 .
(14)
.
(14)
Вероятность пожара в течение времени t
![]() .
(15)
.
(15)
Среднее время ![]() до
первого пожара можно определить следующим образом [2]
до
первого пожара можно определить следующим образом [2]
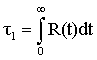 .
(16)
.
(16)
Подставляя выражение (14) в (16) и вычисляя интеграл получим
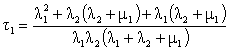 .
(17)
.
(17)
Дисперсию времени до первого пожара можно определить, пользуясь выражением [3]
![]() ,
(18)
,
(18)
где
![]() .
(19)
.
(19)
Подставим (3), (4) и (5) в (16) и находим:
![]() .
(20)
.
(20)
Подставляя значение ψ(s), полученное по формуле
(17) в (15) находим ![]() .
.
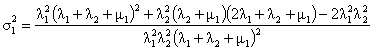 .
(21)
.
(21)
В том случае, если выполняется условие:
![]() ,
(22)
,
(22)
тогда
![]() .
(23)
.
(23)
Полученные в работе формулы позволяют оценить пожароопасность любого участка сети защищаемого автоматическими выключателями или любой другой защитной аппаратурой, действующей на отключение, задавать нормы надежности на защитную аппаратуру, при которой обеспечивается нормируемый уровень пожарной безопасности [4].
Пример. Интенсивность появления токов КЗ в защищаемой автоматическим выключателям сети 220 В жилой квартиры λ1 = 5,2 10-5 ч-1, а μ1 = 1/d1 = 17857 ч-1 (d1 - среднее время срабатывания защитного коммутационного аппарата); интенсивность отказов в срабатывании автоматического выключателя λ2 = 5,7·-6 ч-1
Определить: среднее
время до первого пожара τ1, стандарт этого времени ![]() , вероятность возникновения пожара в течение времени t=8760ч и сравнить полученное значение Q(8760) с нормируемой величиной Q0(8760)=1×10-6;
вероятность нахождения системы в каждом из возможных состояний
, вероятность возникновения пожара в течение времени t=8760ч и сравнить полученное значение Q(8760) с нормируемой величиной Q0(8760)=1×10-6;
вероятность нахождения системы в каждом из возможных состояний ![]() ,
, ![]() ,
, ![]() и
и
![]() ,
t=(1¸5)×105 ч .Построить график функции вероятности безопасной работы
системы
,
t=(1¸5)×105 ч .Построить график функции вероятности безопасной работы
системы ![]() , используя формулу (14) и формулу
(23).
, используя формулу (14) и формулу
(23).
Используя исходные
данные примера, формулы (17), (18) и (15), находим: τ1=194669
ч, ![]() =176489 ч, Q(8760)=9,66×10-3.
Сравнивая найденное значение с нормируемым
Q0(8760)=1×10-6, можно сделать вывод, что в данном примере пожарная
безопасность сети не обеспечивается.
=176489 ч, Q(8760)=9,66×10-3.
Сравнивая найденное значение с нормируемым
Q0(8760)=1×10-6, можно сделать вывод, что в данном примере пожарная
безопасность сети не обеспечивается.
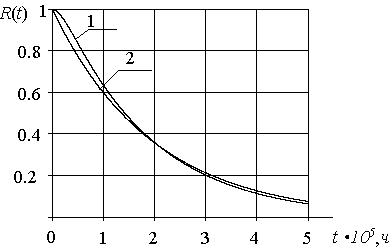
Функция вероятности
безопасной работы ![]() приведена на рис.1. Кривая 1
построена с помощью формулы (14), а кривая 2 с помощью формулы (23).
приведена на рис.1. Кривая 1
построена с помощью формулы (14), а кривая 2 с помощью формулы (23).
|
|
|
|
|
|
Рисунок 1.
Вероятность нахождения
системы в каждом из возможных состояний ![]() ,
, ![]() ,
, ![]() и
и
![]() приведены
на рис.2 и рис.3, кривая 1 получена с помощью формулы (7), кривая 2 - (8),
кривая 3 - (12) и кривая 4 - (13) для t=(1¸5)×105 ч.
приведены
на рис.2 и рис.3, кривая 1 получена с помощью формулы (7), кривая 2 - (8),
кривая 3 - (12) и кривая 4 - (13) для t=(1¸5)×105 ч.
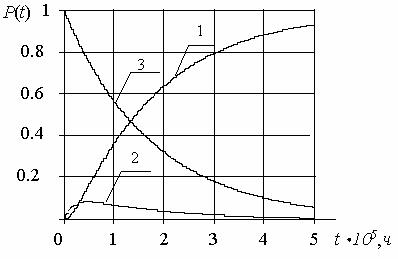
Рисунок 2.
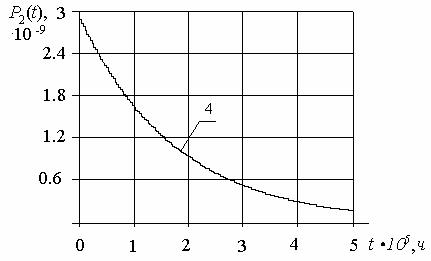
Рисунок 3.
ЛИТЕРАТУРА
1. А. С. Забиров. Пожарная опасность коротких замыканий. - М.: Стройиздат, 1980. - 137 с.
2. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Математические методы в теории надежности. - М.:1965.-524 с.
3. Креденцер Б. П. Прогнозирование надежности систем с временной избыточностью. - К.: Наук, думка, 1987.-240 с.
4. ГОСТ 12.1.004-91. Пожарная безопасность. Общие требования. Издательство стандартов. - 72 с.