Первое, что научился измерять человек, - это протяженность, длину. В начале людей удовлетворяли субъективные меры длины, которые устанавливал правитель данной страны (это, в частности, отразилось в названии линейки, которая по-английски именуется "рулер", что означает "правитель"; отсюда же и рулетка). Так, например, английский ярд был определен как расстояние от конца носа короля до большого пальца его правой вытянутой руки. Позднее изготовили пруток из бронзы, равный этой величине, он служил эталоном ярда.
В средние века в Европе за единицу измерения длины была принята мера, которая определялась следующим образом. Шестнадцать человек становились в затылок друг другу так, что пятка предыдущего касалась концов пальцев ноги стоящего за ним. Одна шестнадцатая длины такой "цепочки" составляла "фут", что по-английски означает "нога", "ступня". При определении, чему равен фут, меньшая длина ступни одного человека компенсировалась большей длиной ступни другого, поэтому средние значения фута мало отличались друг от друга.
Существовали курьезные меры длины. Так, при покупке земли индейцы в качестве единицы измерения принимали территорию, которую человек мог обойти или обежать за один день. Поэтому покупатели обычно нанимали для этой цели самого быстрого бегуна. (Вспомните аналогичную историю, описанную Л. Н. Толстым в рассказе "Много ли человеку земли нужно".) В России субъективными мерами длины были пядь, шаг, локоть. Большие расстояния измерялись полетом стрелы. С развитием торговли и ремесел появились объективные узаконенные меры длины. В России такой мерой стал аршин. Три аршина составляли сажень, 500 саженей - версту (1,0668 км).
В конце восемнадцатого века группа французских ученых предложила метрическую систему мер "на все времена и для всех народов". Она строилась на двух основных единицах: метре и килограмме с производными и десятичными подразделениями. Благодаря простоте и удобству применения метрическая система мер была принята многими странами, в том числе и Россией. В качестве единицы длины - метра была принята одна сорокамиллионная часть земного меридиана, проходящего через Париж. В конце XVIII века специальная экспедиция по поручению Французской академии наук произвела измерение длины отрезка земного меридиана и установила, чему равен метр. На основе полученных данных в 1799 году был изготовлен эталон метра в виде платиновой линейки шириной около 25 мм и толщиной около 4 мм.
Основным недостатком эталона метра было то, что его нельзя было бы вновь воспроизвести (в случае уничтожения) из-за погрешностей геодезических измерений. Тем не менее в 1872 году Международная метрическая комиссия решила принять имеющийся эталон метра в качестве исходной меры длины. Была изготовлена из сплава платины и иридия 31 копия метра. Копия №6 была объявлена международным прототипом метра. Он и две его контрольные копии хранятся в международном бюро мер и весов в Севре (пригород Парижа). Другие копии были розданы странам участницам I Генеральной конференции по мерам и весам. России достались копии №11 и №28. Они хранились во Всесоюзном научно-исследовательском институте имени Д. И. Менделеева в Ленинграде.
В 1960 году XI Генеральная конференция по мерам и весам решила вернуться к естественной воспроизводимой единице длины и дала новое определение метра. Ее резолюция гласит: "...конференция, принимая во внимание, что международный прототип не определяет метр с точностью, достаточной для современных потребностей, и что, с другой стороны, желательно принять естественный и неразрушимый эталон, решает: метр - длина, равная 1650763,73 длины волн в вакууме излучения... атома криптона-86". Введение нового эталона длины повысило точность измерения в сто раз. На основании правил, приложенных к определению метра, в любой стране можно воспроизвести современный эталон длины. Для этой цели служит специальный прибор - компаратор. С его помощью можно изготовить образцовые меры метра из какого-либо стойкого сплава.
После того как единица измерения выбрана, измерить длину нетрудно. Надо просто посмотреть, сколько раз метр (или какая-либо его часть) укладывается на измеряемой величине. А что делать, если нужно измерить расстояние до объекта, расположенного в горах или на сильно пересеченной местности?
Тогда на помощь приходит другой метод определения длины, называемый триангуляцией. Из двух точек А и В, расстояние между которыми известно, находят направления на объект С, расстояние до которого надо определить. В образовавшемся треугольнике АВС известны одна сторона (АВ) и два угла. По этим трем величинам можно найти любой другой элемент треугольника, в частности расстояние до объекта С.
Именно методом триангуляции воспользовались французские ученые, когда измеряли отрезок меридиана, проходящего через Париж. Раньше этот метод был единственным для определения земных расстояний. Теперь существуют еще и другие способы, один из них - аэрофотосъемка.
Во многих местах до сих пор сохранились триангуляционные вышки, и вы можете встретить их, гуляя в окрестностях родного города. В Москве одна такая вышка стоит на Профсоюзной улице между станциями метро Калужская и Беляево. Она отмечает самую высокую точку столицы России.
Непосредственное измерение длины и триангуляция дают одинаковые результаты, когда ими пользуются на Земле. Поэтому естественно распространить метод триангуляции на определение дальности до космических объектов. Так, например, вычисляется высота полета искусственного спутника Земли; так же в свое время было определено расстояние до нашего естественного спутника - Луны. Позже оно было уточнено локацией: сначала радио -, а затем лазерной. Так как скорость радио и световых волн нам известна, то по времени, которое проходит от посылки сигнала до его возвращения после отражения от поверхности Луны, можно определить дальность до нашего естественного спутника (путь, как известно, равен скорости, умноженной на время).
Планеты и Солнце находятся так далеко от нас, что видны с любой точки земной поверхности практически под одним и тем же углом. Поэтому, чтобы найти расстояние до них методом триангуляции, необходимо большее "базовое расстояние", чем диаметр Земли. Им может служить некоторый путь, проходимый Землей в ее годовом движении вокруг Солнца. Этим же способом можно найти дальность до ближайших звезд. Если направить телескоп на некую звезду один раз зимой, а другой - летом, то можно с достаточной точностью определить угол, а следовательно, и расстояние до звезды. (Диаметр земной орбиты известен).
А как быть с очень далекими звездами? Здесь на помощь приходит другой метод, связанный с тем, что чем дальше находится звезда от нас, тем более тусклой она выглядит. Если для ближайших звезд, расстояние до которых известно, установить зависимость светимости от расстояния, то по степени яркости любой звезды, пользуясь полученным законом, можно определить, как далеко она от нас расположена.
Данные о диаметре нашей Галактики позволяют определять еще большие межгалактические расстояния. Размеры всех галактик примерно одинаковы. Поэтому, зная угловой размер какой-либо галактики, то есть тот угол, который она занимает на небосводе, и ее диаметр, можно вычислить расстояние до этой галактики.
Теперь о том, как определяют малые протяженности.
Метр легко разделить на тысячу частей. Немного труднее разделить миллиметр на тысячу частей, для этого нужен хороший микроскоп. Так мы получим микрометр (микрон) - миллионную часть метра. Дальнейшее деление уже производить трудно, так как из-за дифракции невозможно увидеть объект меньше, чем длина волны видимого света (около 5*10-7 м).
С помощью электронного микроскопа можно увидеть и измерить объекты, имеющие размеры до 10-8 м. Чем меньше длина волны излучения, тем более мелкие предметы мы можем "увидеть" и измерить. Так, например, гамма-лучи позволяют "рассматривать" объекты, размеры которых не превышают 10-11 м.
Для определения размеров атомных ядер применяют иные методы: измеряют так называемое эффективное поперечное сечение ядер. Его можно найти, пропуская пучок частиц высокой энергии через тонкую пластинку вещества и измеряя число частиц, не прошедших сквозь нее. Отношение числа не прошедших частиц ко всеми спущенным пропорционально отношению площади, занимаемой ядрами атомов, к площади пластинки. Подобные эксперименты показали, что радиусы ядер имеют порядок 10-15 м. Единица длины, равная 10-15 м, называется ферми в честь известного итальянского физика Энрико Ферми (1901-1954).
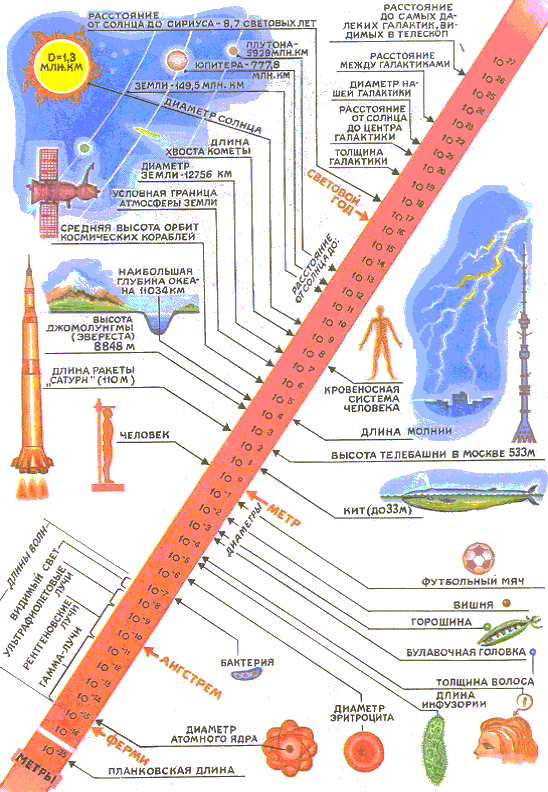
"При решении научных проблем ученому всегда приходится в своем воображении ясно представлять величину... тех физических величин, которые служат для описания изучаемого явления... Поэтому надо приучать смолоду ученых, чтобы символы в формулах, определяющие физические величины, всегда представляли для них конкретные, количественные значения. Для физика, в отличие от математика, как параметры, так и переменные величины в математическом уравнении должны являться конкретными количествами", - говорил академик П. Л. Капица. Именно порядок размеров различных физических объектов показан на рисунке. Чтобы поместить все представленное многообразие на одном рисунке, применена логарифмическая шкала - два соседних деления обозначают размеры, отличающиеся друг от друга в 10 раз. 100 - один метр, 101 - десять метров, 102 - сто метров и т. д.
И в заключение еще одна цитата. Эту мысль высказал наш великий соотечественник Дмитрий Иванович Менделеев (1834 - 1907): "В природе мера и вес суть главные орудия познания. Наука начинается тогда, когда начинают измерять". И первой подчинившейся человеку мерой окружающего его мира была длина, линейный размер, протяженность.
