Сожалея об ограничениях, которые накладывает на жителей земли существование в трехмерном пространстве, выдающийся поэт и историк Валерий Брюсов в стихотворении "Мир N измерений" писал:
"Высь, ширь, глубь. Лишь три координаты. Мимо них где путь? Засов закрыт".
Безусловно, у обитателей четырехмерного мира было бы больше возможностей для поступков и действий, чем у нас. Вот только один пример: в подобном мире можно сделать операцию на сердце, не вскрывая грудную клетку человека. Поясню сказанное. Нарисуйте на листе бумаги окружность и поставьте карандаш острием на бумагу вне окружности. Двигая карандаш по листу, попробуйте дотронуться до центра окружности, не пересекая ее. Сделать это можно, лишь оторвав карандаш от бумаги, то есть выведя его в третье измерение.
Подобно тому как в пространстве трех измерений точка может войти в круг и выйти из него, не при касаясь к окружности, так в пространстве четырех измерений тело может проникнуть во внутрь сферы или выйти из нее, не повреждая поверхность сферы. Следовательно, все закрытое, всякие внутренние области в нашем трехмерном мире открыты для обозрения или действия из четвертого измерения.
Таким образом, известный поэт в какой-то мере прав в своем критическом отношении к среде нашего обитания, но одновременно и не прав. Жить в одномерном или двухмерном пространстве было бы еще хуже. Геометрические объекты там не имеют объемов, веревку нельзя завязать в узел и т. п.
Вернемся теперь в привычный нам трехмерный мир и поговорим о его объемных характеристиках.
Вычислять объемы нас учат в средней школе: мы умеем находить величину куба, шара, цилиндра, конуса и других простейших тел. Но когда-то подобные задачи считались очень сложными. Архимед, определивший соотношение между объемом цилиндра и вписанного в него шара, считал полученный результат настолько важным, что даже завещал выбить найденное им соотношение (3:2) на своей могильной плите.
Все, связанное с объемом, интересует не только математиков и физиков. Уделяют внимание этой теме и писатели. У Бориса Пастернака есть такие строчки, посвященные любимой всеми нами книге: "Книга есть кубический кусок горячей, дымящейся совести - и больше ничего".
В различных литературных произведениях мы встречаемся с теми или иными объемными мерами. Пинта, кварта,галлон, бушель, четверть, штоф, шкалик, бутылка... Что они означают? Первые четыре меры приняты в англоязычных странах, последние существовали в России до введения метрической системы мер. 1 бочка (491,96 л) равнялась 40 ведрам (12,299 л). 1 ведро делилось на 4 четверти (3,0748 л), или на 10 штофов (1,2299 л), или на 100 чарок (0,12299 л), или на 200 шкаликов (0,0615 л). 1 четверть вмещала 5 водочных(пивных) бутылок или 4 винных.
Между английскими мерами тоже существуют определенные соотношения. Например, 1 кварта = 1/4 галлона = 2 пинты, но в Англии и США одинаковые по названию меры объема имеют разные значения. Скажем, английский галлон равен 4,54609 л, американский же - для жидкостей 3,78543 л, а для сыпучих веществ 4,405 л; британский бушель равен 36,3687 л, а американский - 35,2393.
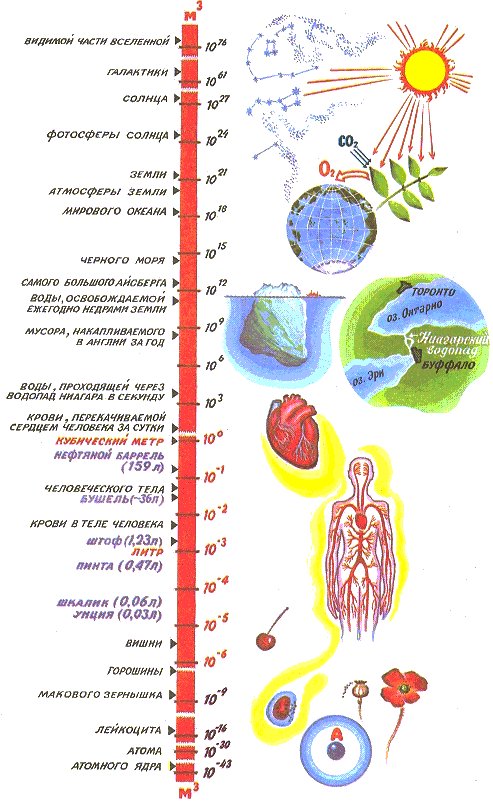
Единица измерения объема - кубический метр. Шкала на рисунке, посвященной объемам, логарифмическая. В центральной части шкалы (цифры выделены красным цветом) два соседних деления отличаются друг от друга по величине в десять раз, в других ее частях (синий цвет) - в тысячу раз (103). Такой масштаб позволил изобразить на одном рисунке многие объемные характеристики окружающего нас мира; от объема атомного ядра до объема всей видимой части Вселенной. Ее величина выражается числом 1076. Это очень большое число. Попробуем его себе представить. Пусть есть путь, длина которого, скажем, в сантиметрах выражается числом 1076. Чтобы пробежать это расстояние свету, движущемуся со скоростью 300000 километров в секунду, потребуется 1058 лет, а наша Вселенная существует "всего" 5*1010 лет.
Или такой пример. Объем атомного ядра 10-43 м3. Следовательно, в одном кубическом метре может поместиться 1043 атомных ядер, а в объеме Солнца - 1070 ядер. Это число в миллион раз меньше числа 1076, выражающего объем Вселенной.
На рисунке вы найдете объемы Солнца и Галактики, человеческого тела и самого большого айсберга, атмосферы земли, макового зернышка, футбольного мяча и много другой информации для сопоставления и размышления.
