 , см. 2.3.2.
, см. 2.3.2.
7. НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Сложные технические объекты (системы), рассчитанные на длительный срок службы, создаются, как правило, ремонтируемыми. В разделе 2 дано толкование основных показателей надежности восстанавливаемых объектов (элементов): средняя наработка на отказ; параметр потока отказов; среднее время восстановления; интенсивность восстановления; коэффициенты готовности и оперативной готовности. В данном разделе рассматривается методика анализа надежности восстанавливаемых систем при различных схемах включения элементов.
Переход системы из неработоспособного (предельного) состояния в работоспособное осуществляется с помощью операций восстановления или ремонта. К первым, в основном, относятся операции идентификации отказа (определение его места и характера), замены, регулирования, заключительных операций контроля работоспособности системы в целом. Переход системы из предельного состояния в работоспособное осуществляется с помощью ремонта, при котором происходит восстановление ресурса системы в целом. Рассмотрим, к примеру, вакуумный выключатель. Вакуумная камера, не подлежащая восстановлению, при отказе заменяется исправной, то есть восстановление работоспособности выключателя происходит путем замены отказавшей камеры. При отказе в том же выключателе электромагнитного (или пружинного) привода восстановление работоспособности выключателя может производиться путем ремонта привода или замены его исправным. В обоих случаях требуется произвести регулировку привода и проверить функционирование выключателя в целом, осуществив контрольные операции "включить"-"отключить".
При анализе используем ряд наиболее часто вводимых допущений.
 , см. 2.3.2.
, см. 2.3.2.
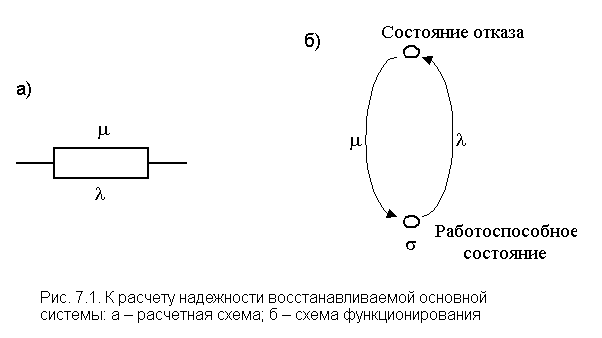
Данная система с интенсивностью l стремится принять состояние отказа, а с интенсивностью m - перейти в работоспособное состояние.
В табл. 7.1 даны заводские параметры l и m для силовой высоковольтной аппаратуры.
Таблица 7.1
Параметры l и m для
некоторых высоковольтных устройств
|
|
|
|
|
| Трансформатор силовой, U1н = 110 кВ |
|
|
|
|
|
|
|
|
|
|
|
| Разъединитель, Uн = 35...220 кВ |
|
|
|
|
|
|
|
|
|
|
|
Обозначим устойчивые состояния системы индексами:
1 - отказ, то есть система находится в состоянии восстановления с интенсивностью восстановления m = const;
0 - работоспособное состояние с
параметром потока отказов
w = const, w =l .
Для анализируемой системы с учетом принятых допущений возможны четыре вида перехода из состояния в момент времени t в состояние в момент времени (t + D t):

Указанные переходы можно представить в
виде графа перехода состояний системы с восстановлением (рис.
7.2).
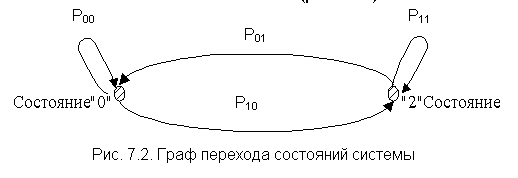
Графу перехода состояний [13] соответствует матрица переходных вероятностей 2 х 2:
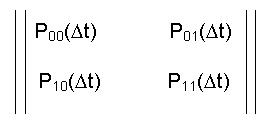 (7.1)
(7.1)
Диагональные элементы этой матрицы соответственно определятся как вероятность безотказной работы на отрезке Dt:
![]()
и вероятность продолжения восстановления системы на отрезке Dt :
![]() .
.
Воспользуемся формулой разложения
функции ![]() в ряд [11]:
в ряд [11]:
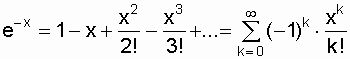 .
.
В высоконадежных элементах l<![]() 1/ч, тогда при
разложении в ряд функции Р00(D t), сохраняя высокую точность
расчета можно ограничиться только двумя первыми членами ряда. Пусть
l=
1/ч, тогда при
разложении в ряд функции Р00(D t), сохраняя высокую точность
расчета можно ограничиться только двумя первыми членами ряда. Пусть
l= ![]() 1/час, Dt = 1 час, тогда
1/час, Dt = 1 час, тогда
 .
.
![]()
Таким образом, запишем
![]() .
.
Соответственно
![]() .
.
Из свойств матрицы следует, что сумма элементов каждой строки матрицы равна единице, как сумма вероятностей появления несовместимых составляющих полную группу событий [13], откуда следует:
Р00(D t) + Р01(D t) = 1; Р01 = 1 - Р00(D t) = l D t + 0(D t);
Р11(D t) + Р10(D t) = 1; Р10 = 1 - Р11(D t) = m D t + 0(D t).
Для составления уравнений вероятностей состояний системы следует записать формулу полной вероятности для каждого столбца матрицы [11, 13, 21]:
![]() - для первого
столбца;
- для первого
столбца;
![]() - для второго
столбца,
- для второго
столбца,
где P0(t) - вероятность нахождения системы в нулевом (работоспособном) состоянии в момент времени t; P1(t) - вероятность нахождения системы в состоянии "1" (отказа) в момент времени t.
Используем запись производной функции f(x):
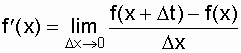
и по аналогии с этим выражением для нашего случая запишем:
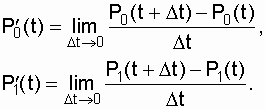
В эти выражения подставим раскрытые
формулы полных вероятностей ![]() и
и ![]() , произведем
соответствующие преобразования и получим систему двух дифференциальных
уравнений относительно вероятностей пребывания системы в состояниях "0" и
"1":
, произведем
соответствующие преобразования и получим систему двух дифференциальных
уравнений относительно вероятностей пребывания системы в состояниях "0" и
"1":
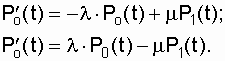
![]() (7.2)
(7.2)
При начальных условиях Р0(t = 0) = 1; Р1(t = 0) = 0, в начальный момент времени (t = 0) восстанавливаемая система работоспособна - находится в состоянии "0". Решение дифференциальных уравнений дает
 . (7.3)
. (7.3)
Вероятность работоспособного состояния системы в момент времени t представляет собой функцию готовности G(t). Функция готовности - это вероятность работоспособного состояния восстанавливаемой системы в определенный момент времени t. Этот показатель является комплексным показателем надежности, оценивающим два свойства системы - безотказность и ремонтопригодность. Заметим, что G(t) дает оценку не за весь период от 0 до t, а только в заданный момент времени t, поскольку до этого система могла находиться как в работоспособном (0), так и в неработоспособном (1) состояниях.
На рис. 7.3 построен график: ![]() при
при ![]() .
.
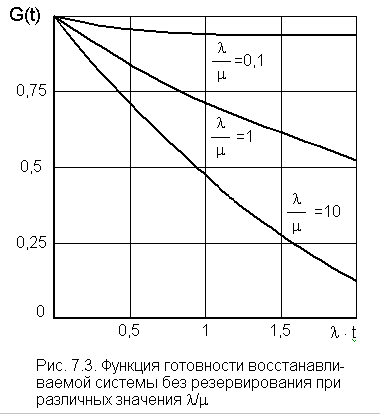
Предположив l = const, можно наглядно увидеть
насколько повысится надежность системы за счет увеличения m (сокращения времени
восстановления ![]() ) для определенного
времени t. Например, при увеличении m в десять раз для момента lЧ t =1надежность повысится
с
) для определенного
времени t. Например, при увеличении m в десять раз для момента lЧ t =1надежность повысится
с
G(t) = 0,41 до G(t) =
0,95. Для высоконадежных систем, к примеру, трансформатора, когда:
l < ![]() 1/ч,
m >
1/ч,
m > ![]() 1/ч, оценку
надежности целесообразно определять за год эксплуатации. В этом случае
удобно пользоваться коэффициентом готовности.
1/ч, оценку
надежности целесообразно определять за год эксплуатации. В этом случае
удобно пользоваться коэффициентом готовности.
Определим предельное значение G(t)по выражению (7.3):
![]() . (7.4)
. (7.4)
Асимптотическое значение функции готовности при t (r) Ґ и есть коэффициент готовности.
Таким образом, коэффициент готовности представляет собой вероятность того, что система окажется работоспособной в произвольный момент времени, кроме планируемых периодов, в течение которых использование системы по назначению не предусматривается.

Пример. Имеется восстанавливаемая
система, у которой параметр потока отказов l = ![]() 1/ч = const, средняя
интенсивность восстановления
1/ч = const, средняя
интенсивность восстановления ![]() 1/ч. Определить, на
сколько повысится надежность этой системы за счет более высокой
организации работы ремонтного персонала, если интенсивность восстановления
системы повысилась вдвое (сократилось вдвое время
восстановления).
1/ч. Определить, на
сколько повысится надежность этой системы за счет более высокой
организации работы ремонтного персонала, если интенсивность восстановления
системы повысилась вдвое (сократилось вдвое время
восстановления).
Решение.![]() ч;
ч; ![]() 50 ч.
Коэффициент готовности системы до улучшения организации труда ремонтного
персонала составлял
50 ч.
Коэффициент готовности системы до улучшения организации труда ремонтного
персонала составлял
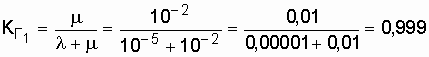 .
.
При улучшенной организации труда
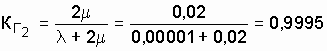 .
.
По сумме затрат, связанных с улучшением организации труда и экономического эффекта от повышения надежности (улучшения ремонтопригодности), можно сделать вывод о целесообразности такого способа повышения надежности системы.
7.2. Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
Система, состоящая из N последовательных
восстанавливаемых элементов, отказывает, когда отказывает любой из
элементов системы. Предполагаются простейшие потоки отказов и
восстановлений ![]() . Как показано в
[15, 19], при заданных допущениях и известных значениях коэффициентов
готовности каждого из последовательно включенных элементов
. Как показано в
[15, 19], при заданных допущениях и известных значениях коэффициентов
готовности каждого из последовательно включенных элементов ![]() ,
коэффициент готовности системы определяется по выражению
,
коэффициент готовности системы определяется по выражению
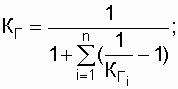

и соответственно при заданных ![]() ,
, ![]()
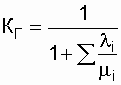 .
.
Пример. Восстанавливаемая система
состоит из трех последовательно включенных элементов с параметрами
надежности: ![]() = 0,6;
= 0,6; ![]() = 0,8;
= 0,8; ![]() = 0,7.
Известно, что
= 0,7.
Известно, что ![]() .
.
Определить коэффициент надежности.
Решение. Подставив заданные значения коэффициентов готовности в выражение КГ системы, получим
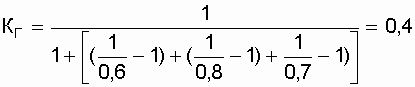 .
.
Здесь же отметим, что в расчетной практике нередко пользуются формулой вероятности безотказной работы неремонтируемой системы с основным соединением элементов, когда
![]() .
.
В этом случае ![]() , что, как видим,
сопряжено с грубой ошибкой. Произведение вероятностей безотказной работы
элементов неремонтируемой системы есть математическая оценка факта
совпадения работоспособного состояния трех, составляющих систему
невосстанавливаемых элементов, то есть работоспособного состояния системы.
Произведение коэффициентов готовности ремонтируемых элементов факта
совпадения работоспособных состояний элементов не отражает
[19].
, что, как видим,
сопряжено с грубой ошибкой. Произведение вероятностей безотказной работы
элементов неремонтируемой системы есть математическая оценка факта
совпадения работоспособного состояния трех, составляющих систему
невосстанавливаемых элементов, то есть работоспособного состояния системы.
Произведение коэффициентов готовности ремонтируемых элементов факта
совпадения работоспособных состояний элементов не отражает
[19].
7.3. Надежность восстанавливаемой дублированной системы
Рассмотрим систему, для обеспечения надежности которой используется дублирование: основной системе добавляется параллельно такая же система. В обеих системах (цепях) параметры потоков отказов одинаковы, l = const, такая же картина и для потока восстановлений, то есть m = const. Такая дублированная система может находиться в трех состояниях:
"0" - обе системы (цепи) работоспособны;
"1" - одна цепь восстанавливается, другая работоспособна;
"2" - обе цепи восстанавливаются. С точки зрения выполнения функциональных задач, возложенных на систему, состояние "2" соответствует отказу. У этой системы возможны семь видов перехода из состояния в момент времени t в состояние в момент времени t + D t:

Указанные переходы изображены на рис. 7.5 в виде графа переходов состояний.
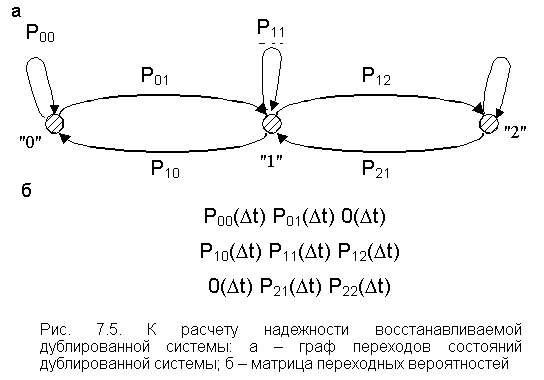
Графу переходов соответствует матрица
переходных вероятностей ![]() . Крайние элементы
побочной диагонали матрицы имеют порядок 0(Dt), так как по исходному
предположению поток отказов в системе простейший, и время восстановления
распределено по экспоненциальному закону. Согласно простейшему потоку в
первой строке матрицы исключается ситуация, когда за время Dt система может перейти из состояния
"0" в состояние "2", Р02(D t) = 0. Рассуждая аналогично, по третьей строке матрицы
запишем Р20(D
t) = 0. При простейшем потоке система за время Dt может из состояния "0" с
вероятностью Р01(D t) перейти в состояние "1" или с вероятностью
Р00(D t)
остаться в состоянии "0". Точно такая же картина соответствует состоянию
"2". С вероятностью Р21(D t) система может перейти в состояние "1" (одна цепь
восстановится) или с вероятностью Р22(D t) останется пребывать в состоянии
"2" (обе цепи неработоспособны - состояние отказа). Элементы первой строки
матрицы переходных вероятностей зависят от режима использования резервной
цепи. Так при нагруженном резерве, работающих обеих цепях, интенсивность
потока отказов равна 2 l
, а при ненагруженном - l
(ненагруженная цепь всегда готова к работе и своих характеристик не
меняет,l= const).
Поэтому
. Крайние элементы
побочной диагонали матрицы имеют порядок 0(Dt), так как по исходному
предположению поток отказов в системе простейший, и время восстановления
распределено по экспоненциальному закону. Согласно простейшему потоку в
первой строке матрицы исключается ситуация, когда за время Dt система может перейти из состояния
"0" в состояние "2", Р02(D t) = 0. Рассуждая аналогично, по третьей строке матрицы
запишем Р20(D
t) = 0. При простейшем потоке система за время Dt может из состояния "0" с
вероятностью Р01(D t) перейти в состояние "1" или с вероятностью
Р00(D t)
остаться в состоянии "0". Точно такая же картина соответствует состоянию
"2". С вероятностью Р21(D t) система может перейти в состояние "1" (одна цепь
восстановится) или с вероятностью Р22(D t) останется пребывать в состоянии
"2" (обе цепи неработоспособны - состояние отказа). Элементы первой строки
матрицы переходных вероятностей зависят от режима использования резервной
цепи. Так при нагруженном резерве, работающих обеих цепях, интенсивность
потока отказов равна 2 l
, а при ненагруженном - l
(ненагруженная цепь всегда готова к работе и своих характеристик не
меняет,l= const).
Поэтому
![]() , (7.6)
, (7.6)
где у - коэффициент, учитывающий
состояние резерва (у = 0 при ненагруженном режиме и у = 1 при
нагруженном).
Используя
разложение степенной функции в ряд, с учетом приближения суммы отброшенных
членов ряда к нулю, запишем
Р00(D t) = 1 - (у + 1) ЧlЧD t. (7.7)
С учетом того, что для первой строки матрицы
Р00(D t) + Р01(D t) = 1,
получим
Р01(D t) = 1 - Р00(D t) = (у + 1) Ч lЧD t. (7.8)
Элементы второй строки матрицы переходных вероятностей (7.5) соответственно запишутся так:
Р10(D t) + Р11(D t) + Р12(D t) = 1;
![]() , (7.9)
, (7.9)
![]() , (7.10)
, (7.10)
![]() . (7.11)
. (7.11)
Элементы третьей строки анализируемой матрицы, с учетом количества ремонтных бригад и многократного восстановления отказавших цепей, соответственно определятся так:
Р21(D t) + Р22(D t) = 1;
![]() ; (7.12)
; (7.12)
![]() , (7.13)
, (7.13)
где r - число ремонтных бригад (r = 1 или r = 2).
При дублировании с восстановлением возможны шесть вариантов задач анализа надежности такой системы:
1) система с нагруженным резервом до первого отказа (у = 1, r = 0);
2) система с ненагруженным резервом до первого отказа (у = 0, r = 0);
3) многократно восстанавливаемая система с нагруженным резервом и одной ремонтной бригадой (у = 1, r = 1);
4) многократно восстанавливаемая система с нагруженным резервом и двумя ремонтными бригадами (у = 1, r = 2);
5) многократно восстанавливаемая система с ненагруженным резервом и двумя ремонтными бригадами (у = 1, r = 2);
6) многократно восстанавливаемая система с ненагруженным резервом и одной ремонтной бригадой (у = 0, r = 1).
Для определения Р0(t),
Р1(t), ![]() необходимо составить
и решить систему трех дифференциальных уравнений
необходимо составить
и решить систему трех дифференциальных уравнений
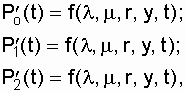 (7.14)
(7.14)
где ![]() - постоянные
коэффициенты.
- постоянные
коэффициенты.
Для этого на основе свойств столбцов матрицы необходимо записать выражения формул полных вероятностей Р0(t + D t), Р1(t + D t), Р2(t + D t), затем записать производные для выражений вероятностей нахождения системы в состояниях "0", "1", "2" и свести их в систему уравнений:
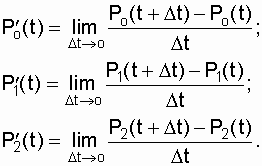 (7.15)
(7.15)
Формулы полных вероятностей запишутся на основе матрицы (7.5) соответственно:
по первому
столбцу ![]()
по второму столбцу ![]() ;
;
по третьему столбцу![]() .
.
Подставив в эти выражения соответствующие значения переходных вероятностей, получим систему из трех дифференциальных уравнений (7.15) с четырьмя постоянными коэффициентами l , m , r, у.
Определение искомых вероятностей
пребывания системы в состояниях "0", "1" и "2" в момент времени t
производится при следующих начальных условиях: Р0(t = 0) = 1;
Р1(t = 0) = 0; Р2(t = 0) = 0, то есть система
первоначально включается в работу с обоими исправными цепями. Решение
системы (7.15) подробно изложено в специальной литературе, например в
[13]. Искомое выражение функции готовности анализируемой системы при
найденных значениях Р0(t), Р1(t), Р2(t)
на основе известного свойства ![]() удобнее записать в
виде:
удобнее записать в
виде:
![]() .
.
Анализируемая система получается
высоконадежной. Даже в нерезервированной восстанавливаемой системе
при 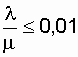
![]()