Формы совместного движения воздуха и воды многообразны – от движения двух сплошных потоков, взаимодействующих на поверхности раздела, до движения потока пены, в котором обе фазы образуют сложную и неустойчивую структуру. На основании методики, описанной в работе [1], рекомендуется определять вид течения газожидкостной смеси в зависимости от двух характерных параметров: истинного газосодержания j и числа Фруда Fr. Расчеты показали, что условиям гидрошахт соответствует пузырьково-пробковый режим течения газожидкостной смеси (j = 0,25 – 0,51 и Fr = 3,2 – 6,3).

Критерии подобия определялись с помощью теории размерностей. Было установлено, что наиболее существенными факторами пузырьково-пробкового режима течения газожидкостной смеси являются: r ₀ – плотность жидкой фазы; D r – дифференциальная плотность; μ', μ"– ρоответственно динамический коэффициент вязкости жидкой и газообразной фазы смеси; σ – коэффициент поверхностного натяжения; g – ускорение свободного падения; V₀ – характерная скорость; V' – скорость жидкой фазы смеси; V" – скорость газообразной фазы смеси; l₀ и l – характерные геометрические размеры трубы; p₀ – давление в характерном сечении трубы; τ – характерное время процесса. С учетом принятых обозначений уравнение связи исследуемого процесса можно представить в виде

ƒ ( l₀, V₀, ρ₀, D ρ, μ', μ", σ, g, V', V", p₀, τ, l ) = 0 , (1)

где перечисленные величины имеют следующие размерности: [l₀]=[l]=м; [ρ₀]=[D ρ]=κг/м³; [μ']=[μ"]=κг/м× с; [σ]=кг/с²; [g]=м/с²; [р₀]= кг/м^.с²; [τ]=c.

При определении критериев подобия независимыми переменными уравнения (1) приняты l₀, V₀, ρ₀, а основными единицами измерения [L] = м, [M] = кг, [T] = c.

Согласно первой p – теореме подобия после замены размерных величин на безразмерные в уравнении (1) получаем уравнение связи, которое содержит m – k = 10 безразмерных p – комплексов (критериев), где m = 13 – число параметров, влияющих на процесс и введенных в уравнение, k = 3 – число независимых параметров, принятых за основные. Опуская промежуточные вычисления для каждого p – комплекса, запишем следующие математические выражения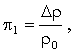

где 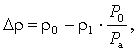ρ₁ – плотность воздуха при нормальных условиях, Р₀ – давление воздуха на участке незаполненного водой вертикального трубопровода.

где Re' – число Рейнольдса для жидкой фазы, в котором в качестве характерного размера l₀ принимается внутренний диаметр d трубопровода, а в качестве V₀ – средняя скорость V потока воды на входе в трубопровод.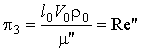

где Rе'' – число Рейнольдса для газообразной фазы, в котором V₀ = V_отн – средняя относительная скорость газового пузыря или пробки; l₀ = d_п – диаметр газового пузыря с учетом истинного газосодержания φ.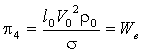

где W_e – критерий Вебера при l₀ = d, V₀ = V.

где Fr – критерий Фруда, если l₀ = d, V₀ = V.

где Ho– критерий гомохронности, если l₀ = h – длина вертикального трубопровода, V₀ = V.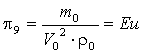

где Eu – критерий Эйлера при V₀ = V.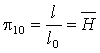

где l = h, l₀ = d.

Для сокращения полученных безразмерных комплексов разделим p ₅ на p ₆ и получим – расходное газосодержание водовоздушной смеси. Умножая p ₁ на p ₇, получим преобразованный критерий Фруда с учетом Архимедовой силы .

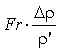Но = ƒ (, Re', Re", We, β, , Eu) (2)

Обеспечить одновременно идентичность всех критериев уравнения (2) практически невозможно, так как в рамках физического моделирования для выполнения условий подобия масштабам одних и тех же величин, входящих в разные критерии, должны быть предъявлены разные требования. Такими критериями являются критерии Фруда, Рейнольдса и Вебера, характеризующиеся противоречивыми соотношениями масштабов по скорости и давлению. Поэтому исследования проводились путем приближенного моделирования [2]. Для этого, используя закон подобия Ньютона, основанный на соотношении сил различной природы с силой инерции, уравнение (2) было исследовано на возможность сокращения числа критериев (малозначимых). На рис. 1 графически показан пузырьково-пробковый режим течения, для которого характерным является поочередное движение в потоке жидкости газовых пузырей и пробок, соразмерных с внутренним диаметром трубопровода. Наиболее существенными силами, воздействующими на газовое образование при направлении течения воды сверху вниз, являются: F_i – сила инерции, [F_i] = [ρ] [V]²[l]²; F_g – сила тяжести с учетом Архимедовой силы, [F_g] = [ρ] [l]³ [g]; F_σ – сила поверхностного натяжения, [F_σ] = [σ] [l]; F_р - сила давления, [F_p] = [p] [l]²; F_μ – сила вязкости, [F_μ] = [μ] [V] [l].

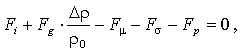
или ,

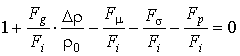или . (3)

Оценим влияние каждого из слагаемых в уравнении (3). Для этого по математическим выражениям критериев вычислены значения интересующих нас комплексов в интервалах рабочих характеристик рассматриваемого процесса (V = 2,36…3,74 м/с, d = 0,2…0,3 м, ρ₀ = 998,2 кг/м³, ρ'' = 1,2 κг/м³, μ' = 1^.10^–3 Па с, μ'' = 0,0132 Па^.с, σ = 0,0723 Н/м, V_отн = 5,7 м/с, Р₀ = 12,8^.10⁴…30,5^.10⁴ Па ):

Fr = 2,84…4,75; ; Еu = 10,6…31,4;

Согласно закону подобия Ньютона, если какой-либо член уравнения на несколько порядков больше других, то это указывает на наличие автомодельности по данным критериям и на потенциальную возможность исключить эти критерии из дальнейшего рассмотрения как не оказывающие существенного влияния на конечный результат. На основании сказанного, искомое приближенное критериальное уравнение рассматриваемого процесса принимает вид

где 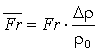– преобразованный критерий Фруда с учетом Архимедовой силы.

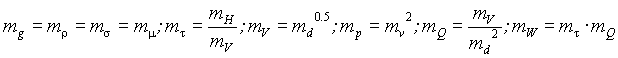где масштаб mt – по времени, m_d – по диаметру, m_н – по длине, m_v – по скорости, m_p – по давлению, m_Q – по расходу, m_w – по объему, m_g – по ускорению свободного падения, m_ρ – по плотности, m_μ – по динамической вязкости, m_σ – по поверхностному натяжению.

Основными масштабами моделирования считаются m_d, m_v и m_ρ, остальные производные. Математические формулы масштабов mt , m_v и m_ρ получены из условий идентичности критериальных чисел Нo, Fr и Eu, а масштабов m_Q и m_w из известных формул определения расхода воды Q в трубопроводе диаметром d через скорость V и объема W через расход Q за время τ.

Таким образом, на основании выше сказанного, возможно физическое моделирование двухфазных потоков жидкости в вертикальных трубопроводах. Так, для исследования процесса заполнения водой трубопроводных сетей сооружена в лабораторных условиях экспериментальная установка – физическая модель системы водоснабжения забоев гидрошахт (рис. 2). Построение установки осуществлялось с учетом следующих численных значений масштабов моделирования, одновременно являющиеся и константами подобия: m_ρ = m_σ = m_μ = m_g = 1, m_d = 6, m_н = 51,25, m_v = 2,45, m_p = 6, m_τ = 21, m_Q = 88,2, m_w = 1845, m_β = 0,6.

Для визуального наблюдения за исследуемым процессом трубопроводы изготовлены из прозрачного материала. Установка оборудована различными приборами для измерения необходимых параметров: давления, скорости, времени, линейных размеров. Комплексы определялись косвенным путем с использованием соответствующих зависимостей, содержащих справочные величины и параметры прямых измерений.

Исследования показали следующее. Во-первых, подтвердился пузырьково-пробковый режим течения газожидкостной смеси в вертикальном трубопроводе системы водоснабжения забоев гидрошахт. Во-вторых, процесс заполнения водой вертикального трубопровода состоит из двух этапов – наполнение водой трубопровода и вытеснения воздуха из смеси. В процессе наполнения водой образуется газожидкостная смесь, уровень которой постепенно увеличивается достигая через время t_нп верхней точки вертикального трубопровода 3' (рис. 2). После наполнения трубопровода газожидкостной смесью, содержащей некоторый объем воздуха в виде отдельных пузырей, пробок, рассредоточенных по всей длине h₁, происходит за время t_вм вымыв (удаление) воздуха потоком воды, поступающего в трубопровод. Эти процессы в общем виде описываются критериальным уравнением (4). В результате обработки на ЭВМ экспериментальных данных параметров и Eu получены эмпирические математические зависимости уравнения (4) для процессов:

наполнения (5)

и вытеснения , (6)

Искомое время заполнения водой вертикального трубопровода t_з можно определить как

t_з = t_нп + t_вм , (7)

где 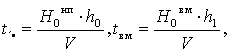h₀ – начальная длина наполняемого водой участка вертикального трубопровода (см. рис.2); h₁ – длина вертикального трубопровода (см. рис.2).

Среднеквадратичная погрешность определения времени t_з по формуле (7) с учетом погрешностей вычислений параметров Н_о^нп, Н_о^вм, h₁, h₀, V составляет не более 17,2 %, что вполне приемлемо для систем управления водоснабжением забоев гидрошахт.

1. Козлов Б.К. Формы течения газожидкостных смесей и границы их устойчивости в вертикальных трубопроводах. Журнал технической физики. – М.: Изд–во АНСССР, 1954.–т.24– вып. 12 – с. 2285 – 2288.

2. Клайн С. Подобие и приближенные методы. Пер. с англ. – М.: Мир, 1986 – 235с.

3. Оголобченко А.С. Экспериментальные исследования процесса заполнения водой трубопроводной сети энергетического водоснабжения забоев гидрошахты. Донецк политехн. ин-т. – Донецк, 1990. – 40 с. – Деп. в УкрНИИНТИ 17.08.90, № 1336 – Ук 90.