Рассмотрим напряженное состояние горного массива, вызванного действием абсолютно твердых целиков, аналогичных по действию жесткого штампа на полупространство.

Пусть жесткий штамп давит на границу полуплоскости Jmz≤0 (рисунок 1) и предположим, что трение между штампом и полуплоскостью отсутствует. Пусть у = f(х) уравнение профиля основания штампа до начала вдавливания в упругую полуплоскость. Если предположить, что штамп может перемещаться только поступательно в направлении нормальному к границе, то профиль его основания после вдавливания будет иметь вид

y = f(x)+c.

Считаем, что f(x) и f^`(x) малые величины, (что вытекает из малости деформаций).

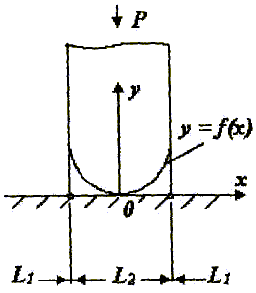
Рисунок 1 – Схема давления

Тогда граничные условия задачи давления штампа на полуплоскость запишутся в виде

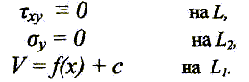
Здесь L – обозначена вся действительная ось OX, на L₁ – участок OX под штампом; на L₂ – остальная (незагруженная часть на L). С учетом [2]:

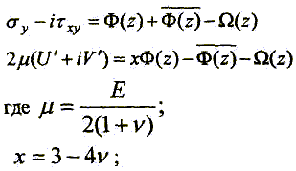
E – модуль упругости;
υ – коэффициент Пуассона вмещающих пород.
Тогда смешанная задача для нижней полуплоскости приводится к следующей краевой задаче для функций Ф(z) и Ω(z).

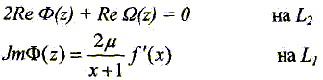
Т. к. функция Ω(z) непрерывна, то из условий Коши-Римана для аналитических функций следует, что Re Ω(z) ≡ 0 на L. Следовательно на всей границе области Ω(z) ≡ 0. Тогда согласно интегральной формуле Коши Ω(z) ≡ 0 во всей нижней полуплоскости. (Этот же результат можно получить, если воспользоваться формулой Келдыша - Седова) Таким образом решение граничной задачи сводится к решению краевой задачи для функции Ф(z)

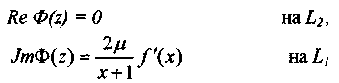
которое дается формулами (1.6, 1.7) где функция α⁺(t) = Х(t) должна быть заменена на X ^-(t) = -α (t).

Рассмотрим частные случаи

2⁰. Действие штампа с закругленным основанием

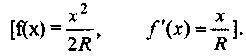
Будем сначала считать, что под действием прижимающей силы весь профиль приходит в соприкосновение с полуплоскостью. Будем иметь неограниченное решение граничной задачи на обоих углах под штампом (x = ±l).

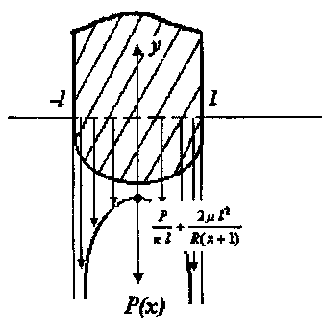
Рисунок 2 – Давление под штампом

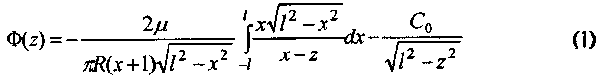
При вычислении интеграла сделаем замену

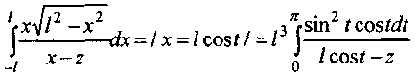
а в последнем универсальную тригонометрическую подстановку

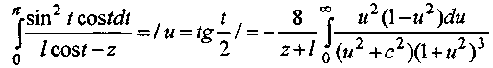
Разложим подынтегральную функцию на простейшие дроби

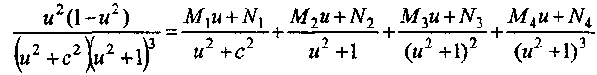
и найдем коэффициенты разложения

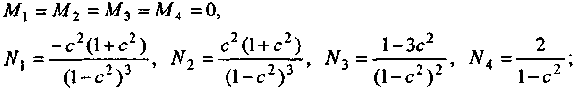
Тогда

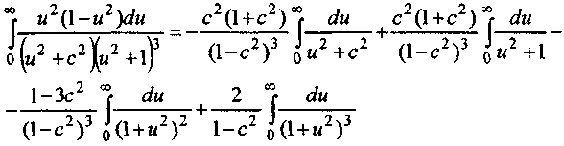
Учитывая, что

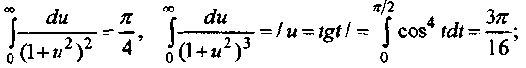
Находим

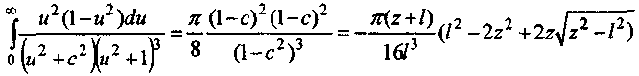
Таким образом

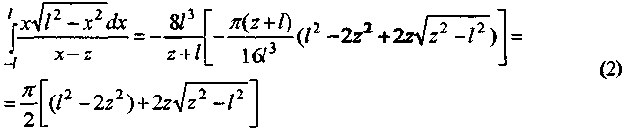
Подставляя (2) в (1) имеем

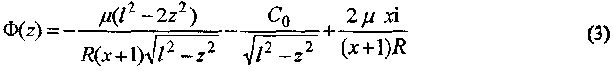
Из (3) следует

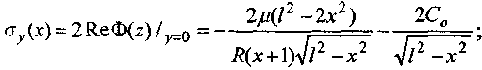
Постоянную C₀ определим из условия

Так как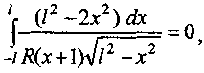

то из соотношения (4) следует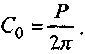

Таким образом

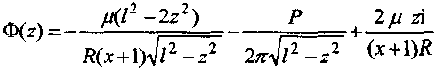
Давление под штампом определяется функцией

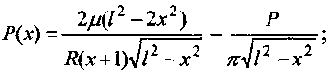
график которой представлен на рисунке 2

Заметим, что полученное решение (5) справедливо в том случае, если P(l)≥0, т. е.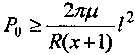

3⁰. При условии задачи 2⁰ предположим, что прижимающая сила не столь велика (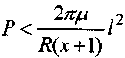), а следовательно в соприкосновение с плоскостью приходит только некоторая часть закругленного профиля на участке (- l₁, l₁).

В этом случае решение дается формулой

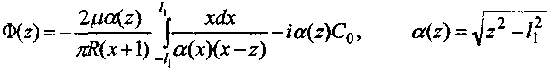
Так как напряжения на бесконечности должны быть ограничены, то C₀=0, а следовательно

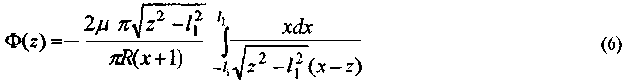
При вычислении интеграла сделаем замену

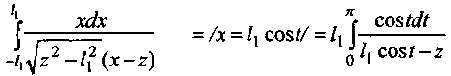
а затем универсальную тригонометрическую подстановку

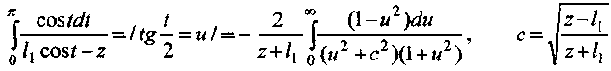
Разложим подынтегральную функцию

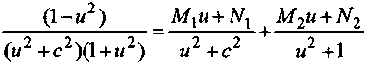
и найдем коэффициенты разложения

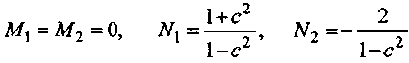
Тогда

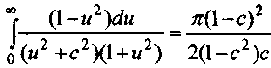
Откуда

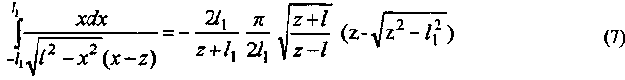
Подставляя (7) в (6) имеем

Следовательно, давление под штампом равно

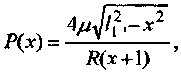
а его распределение показано на рисунке 3.

Используя соотношение

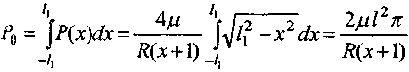
находим связь между l₁ и P₀

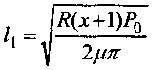
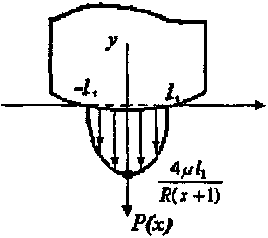
Рисунок 3 – Распределение давления под штампом.