УДК 622.678

ПРОЦЕСС РАЗВИТИЯ ТРЕЩИНЫ ОТ  МАКРОПОВРЕЖДЕНИЙ ПРОБОЕМ В РЕЗИНОТКАНЕВОЙ ЛЕНТЫ ШАХТНОГО КОНВЕЙЕРА КАК ОБЪЕКТ АВТОМАТИЗАЦИИ

Татаринский А.В., студент 5-го курса, Грудачев А.Я., к.т.н., профессор кафедры     ГЗТ и Л

(Донецкий национальный технический университет, г.Донецк, Украина)

Надежность конвейера определяется в частности из возможности предотвращения аварий, которые связаны с повреждением конвейерной ленты, в частности от сквозных пробоев и распространения на их основе трещин, что уменьшит простои и увеличит производительность шахтных конвейеров. Исследование и обоснование процесса развития трещин, позволит сформулировать технические требования для разработки датчиков, определяющих и сигнализирующих о появление трещин, которые в последствии могут быть включены в систему автоматического управления и контроля шахтных конвейеров. Целью данной статьи является разработка математической модели напряженно-деформационного состояния резинотканевой ленты с учетом ее макроповреждений пробоем, что обеспечит основу для создания соответствующего датчика, разработка  которого и является предметом специализации в области автоматизации.

  Если представить изменение скорости распространения трещины по ее длине в полулогарифмических координатах, то на стадии медленного развития эта зависимость представляет собой прямую линию, проходящую под некоторым углом к оси абсцисс (угол tgα=β).  При достижении определенной длины трещины происходит скачкообразный переход к быстрой стадии развития, причем τ₁»τ₂. Анализ полученных экспериментальных данных [1] позволяет сделать вывод о наличии экспоненциальной зависимости скорости роста трещины от ее длины на первой стадии разрушения, т.е.

    v₁=v₀ е^β1, м/с                                            (1)   

Долговечность резинотканевых ленты можно представить в виде:

                                                                                                                                                                                                                   ,с                  (2)

В общем случае долговечность образцов может быть выражена соотношением:

                        τ=be^-Bσ,с                                          (3)   

где    b и В  - постоянные, зависящие от материала;

σ - напряжения в образце.

Используя теорию Маккеавели [2], согласно которой конец трещины в материале имеет характерный (фиктивный) радиус, можно подсчитать напряжение σ₀^тр около вершины трещины по формуле:

                            , кН                                    (4)

где    С_тр - длина трещины, см;

J - некоторый фиктивный радиус трещины, см.

σ_н=σ_экв - начальное напряжение в образце, на момент появления трещины, кН.

Используя известные зависимости получаем формулу:

                                                                                                                                                                (5)

 Можно выделить время распространения трещины в образце:

                                                                                    (6)

где    L₀ - начальная длина трещины.

В резинотканевых лентах могут образовываться трещины, не опасные для нее, т.к. напряжение около их радиусов распространения не превышает разрывного усилия ленты. Трещина не опасна, если

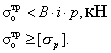
Так как трещина в резинотканевой ленте распространяется в две стороны от условно взятой середина ее образования, тогда напряжения и время распространения трещины в две стороны  для прямолинейного участка ленты, т.е без учета сдвигающих усилий, можно представить  в виде:

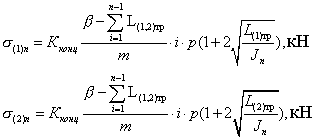
В ленте в одном поперечном сечении может располагаться несколько пробоев (трещин), тогда напряжение в ленте, относительно n-го пробоя:

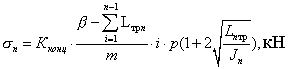                            (7)

при этом разрыве усилие в ленте:                                                                                                                             

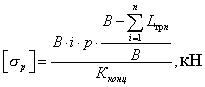                                                                                   (8)

где       -  сумма длин трещин по ширине ленты в одном направлении

распространения;

n - число пробоев в одном направлении ширины ленты;

-      сума длин трещин по ширине ленты в одном направлении, за вычетом той трещины, напряжение около окружности, которой определяется;

        -  коэффициент концентраций напряжения около трещины (пробоя).

              Как граничное условие можно брать напряжение в ленте равное напряжению прочности ленты с учетом коэффициента запаса прочности.  Для наглядного показа существующих напряжений в ленты целесообразно использовать графики (рисунок.1)

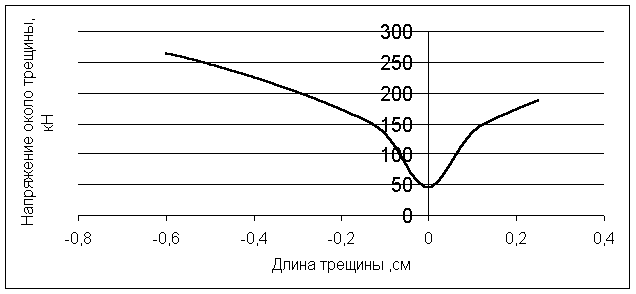
               Рисунок 1- Распространения напряжения от одного соединительного элемента  в ленте при использовании разъемного соединителя типа К28

Список используемых источников

1.  Прочность, устойчивость, колебания. Справочник, т.1, М.,"Машиностроение", 1968,с.575

     2.Перис П., Эрфган Ф. Критический анализ законов распространения  трещин-

       "Техническая механика", М., "Мир", 1963, № 4