Статья взята со страницы кафедры разработки пластовых месторождений полезных ископаемых.

 

РАСЧЕТ ПАРАМЕТРОВ ПОЖАРООПАСНЫХ ЗОН В ВЫРАБОТАННОМ ПРОСТРАНСТВЕ ВЫЕМОЧНОГО ПОЛЯ

Канд. техн. наук В.К.КОСТЕНКО, (НИИГД)

Приведено новое решение задачи о напряженном состоянии горных пород в кровле пласта. На основе теории многослойных плит с учетом переменной мощности слоев, анизотропии и трещиноватости горных пород найдены решения для граничных условий, отражающих полное обрушение кровли и закладку выработанного пространства. Приведены результаты оценки влияния мощности и последовательности чередования слоев, анизотропии свойств пород, их трещиноватости, условий заделки краев.wpe3.jpg (24101 bytes)

Эндогенные пожары — это наиболее трудоемкий при ликвидации и продолжительный вид аварии. Более 90% этих пожаров возникают в труднодоступных частях выработанных пространств действующих или отработанных выемочных полей. Условием зарождения очагов самонагревания и возгорания является наличие пожароопасных зон — полостей в выработанном пространстве, содержащих измельченный уголь, к которым поступает воздух и отводятся продукты реакции. Образование пожароопасных зон связано с зависанием пород кровли над кромкой угольного массива (целика) или над искусственными сооружениями: крепями, кострами околоштрековыми бутовыми или литыми полосами, и т.п. Для предупреждения и тушения пожаров, возникающих в результате самонагревания угля в выработанном пространстве выемочных полей, необходимо знать параметры областей зависания пород кровли пласта, а также места образования и ориентацию трещин, определяющих ее обрушение.

Эта задача решается путем исследования напряженного состояния горных пород кровли разрабатываемого пласта. В работе [1] изложены теоретические основы расчета напряженного состояния горных пород кровли. При этом расчетная схема представлена в виде многослойной плиты в общем случае переменной жесткости и прямоугольной в плане, состоящей из ортотропных породных слоев, находящихся под действием внешней нагрузки и собственной массы. Граничные условия, соответствующие способам управления кровлей закладкой выработанного пространства или полным ее обрушением, соответственно приняты для плиты в виде: два смежных края защемлены (границы угольного пласта), два других или свободно-опертые (закладка), или свободные (обрушение).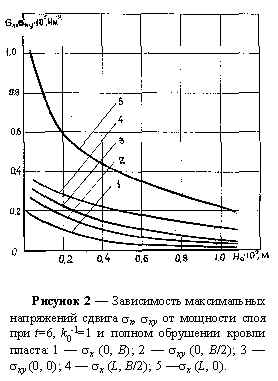wpe2.jpg (21089 bytes)

С использованием приема, заключающегося в представлении полного прогиба в виде суммы двух составляющих: за счет изгиба и сдвига, технической теории многослойных пластин и вариационного метода Ритца получены система линейных алгебраических уравнений, выражения для координатных функций и напряжений с учетом деформаций сдвига.

На основании разработанного алгоритма, который реализован с помощью пакета инженерного проектирования mapleV’ for Windaws’95, проведено исследование сходимости и устойчивости метода решения. Установлено, что сходимость по методу Ритца в данном случае обеспечивается при количестве сочетаний координатных функций n=14, а устойчивость — с необходимой степенью точности. Результаты расчета показали, что влияние деформаций сдвига на напряжения изгиба является незначительным (около 7%). Поэтому для снижения трудоемкости решения задачи вместо системы координатных функций [1], которые подчинены геометрическим условиям по методу Ритца, в дальнейшем использованы балочные степенные функции, точно удовлетворяющие всем граничным условиям, т.е. для условий типа защемление — свободная опора:

. (1)

Для условия типа защемление — свободный край:

, (2)

где k в f(k) принимает значения x, а g в g(k) — y.

Сравнение качественной картины распределения максимальных напряжений по разработанному методу и классическому методу [2], показало, что напряжения совпадают по знаку, а погрешность их отношений в середине защемленных краев и в центре не превышает 10%. Это подтвердило правильность выбора координатных функций и метода решения задачи.

В реальных условиях последовательность расположения слоев горных пород, их мощности и физико-механические свойства меняются в широком диапазоне, поэтому интерес представляет исследование влияния этих параметров на компоненты напряженного состояния кровли.

Рассмотрена одна из наиболее распространенных пожароопасных ситуаций, когда в кровле отрабатываемого пласта оставляют пачку угля. Получены схемы распределения максимальных напряжений в нижнем слое толщи пород кровли пласта в зависимости от общей мощности (толщины) Но кровли и отношения модулей упругости в плоскости напластования горных пород к поперечному их направлению при количестве слоев t=6. Результаты для двух видов граничных условий приведены на рисунках 1–3. При этом варьировались последовательность расположения слоев горных пород, их мощности в пределах от 3 до 110 м и возможных отношений модулей упругости (коэффициентов анизотропии) 1?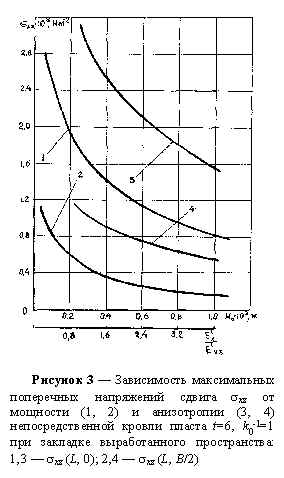 ? 4.wpe4.jpg (23163 bytes)

Как показывают результаты исследований, независимо от порядка расположения слоев горных пород, их мощностей и изменения коэффициента анизотропии, напряженное состояние практически одинаковое на верхней и нижней плоскостях породного слоя, но противоположно по знаку. При этом, с увеличением общей мощности слоя и отношения модулей упругости, величины напряжений уменьшаются. Наибольшими из компонент максимальных напряжений являются поперечные (касательные) напряжения сдвига sxz. Это подтверждает эмпирически установленную закономерность о том, что устойчивость монослоя значительно выше, чем пачки слоев с одинаковыми физико-механическими свойствами и равной суммарной мощностью.

В результате влияния очистных работ в горных породах изначально могут образоваться трещины, которые, естественно, повлияют на изменение механических характеристик кровли, а, следовательно, и на напряженное ее состояние. Для трещиноватых массивов горных пород в зависимости от вида наиболее распространенных в реальных условиях систем трещин учитывая, что они располагаются под углом 0° и 90о к плоскости напластования, использованы выражения для упругих параметров [3], т.е. для систем зияющих трещин:

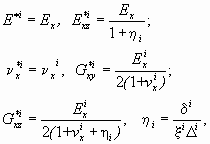, (3)

где — модуль упругости сплошной эквивалентной среды по направлению, совпадающему с плоскостью трещин; — модуль упругости сплошной эквивалентной среды по нормали к трещинам; — модуль сдвига в плоскости трещин; — модуль сдвига в плоскости нормальной к поверхности трещин; — коэффициент Пуассона, определяемой как отношение поперечной деформации в поперечной плоскости к продольной деформации в плоскости трещин; — модуль упругости ненарушенного материала массива, Н/м2; — коэффициент Пуассона ненарушенного материала массива; — ширина раскрытия трещин, м; — расстояние между трещинами, м; —относительная площадь скальных контактов в данной трещине, м2 (согласно [2] среднее значение =3? 10–4 м2).

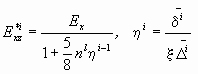Для систем с хаотической трещиноватостью примерно равной мощности и при <<, в отличие от (3), для расчет ведется по зависимости:

, (4)

где ni — число систем трещин; — средняя ширина раскрытия трещин, м; — средняя протяженность ненарушенного материала, приходящегося на одну трещину, м.

С учетом зависимостей (3), (4), для средних значений , получены эпюры распределения напряжений в кровле с двумя видами граничных условий, откуда следует, что, в связи с уменьшением модулей упругости, а, следовательно, ее жесткости, напряженное состояние кровли снижается. При этом уровень напряжений ниже у пород с хаотической трещиноватостью, а напряжения в кровле с зияющими трещинами в направлении их распространения значительно ниже, чем в продольном направлении.

На основании приведенных результатов исследована целостность кровли, для чего сравнивались максимальные напряжения, возникающие в слоях, с предельными для данного типа пород значениями.

Исходным для этих исследований служит распределение напряжений в породах кровли с толщиной Но=3 м, равными параметрами в плане, при количестве слоев t=6, с двумя видами граничных условий, на рисунках 1–3 приведены их максимальные значения.

Анализ результатов для кровли с граничными условиями защемление — свободная опора показывает, что максимальные нормальные напряжения или и продольные напряжения сдвига, т.е. в середине защемленных краев и в начале опертого края соответственно, ниже минимальных предельных их значений на растяжение и сдвиг для угля. В тоже время поперечные напряжения сдвига или , т.е. посередине защемленного края, превышают предельные их значения на всем интервале, а , т.е. в середине опертого края, равны или превышают предельные значения на интервале 24–72 Нм–2. Отсюда следует, что в кровле с вышеуказанными граничными условиями в двух направлениях возникнут поперечные трещины.

С увеличением толщины кровли и отношения модулей упругости ее напряженное состояние снижается (рисунок 1) и при Но>30 м, >4 в середине опертого края, если предельное значение равно 24·105 Нм–2, Но>8 м, >1,4 в середине защемленного края, если предельное значение равно 100 Нм–2 или Но>50 м, если предельное значение равно 24·105 Нм–2, трещины образовываться не будут.

Выше рассматривалась прочность кровли с одинаковыми параметрами в плане, т.е. при kо–1=1. Однако распределение напряжений меняется в зависимости от их отношения, причем они увеличиваются в направлении большой стороны и при kо–1=2 нормальные напряжения больше примерно в 1,5 и 3,0 раза, а поперечные напряжения сдвига — в 2,0 раза. Поэтому в данном случае максимальные нормальные напряжения в точке (L/2, B/2), т.е. в середине рассматриваемого участка кровли, достигнут предельных значений для угля и могут появиться трещины в направлении меньшей стороны, соответствующие напряжения в середине защемленного края приблизятся к предельному значению, а увеличение поперечных напряжений сдвига повлечет за собой увеличение зоны образования трещин.

Напряженное состояние в кровле с граничными условиями защемление —свободный край, естественно значительно выше, чем с предыдущими граничными условиями. Наиболее напряженными точками в кровле, подлежащими анализу для определения ее целостности, являются: для нормальных напряжений s x(L, 0), s x(L, В/2), s x(0, B); для продольных напряжений сдвига s xy(0, 0), s xy(0, В/2) и поперечных напряжений сдвига s xz(L, 0), s xz(L, В/2).

Наиболее напряженными точками, откуда начнут образовываться трещины, являются места защемления краев кровли, где возникают разрушающие нормальные s x и поперечные s xz напряжения сдвига, которые, несмотря на снижение их к свободным краям, на большей части интервала длины превышают соответствующие предельные значения для угля на растяжение, сжатие и сдвиг. Разрушающими являются эти напряжения в средней части защемленных краев, которые, будучи меньше примерно в три раза, с аналогичным законом изменения к свободным краям, также на большей части интервала длины превышают предельные значения, а также продольные напряжения сдвига, отличаясь незначительно по величине в начале и в средней части свободных краев кровли и уменьшаясь к защемленным краям, явятся причиной образования зияющих трещин.

При kо–1=В/2=2,0 максимальные напряжения в направлении большей стороны возрастут в 2,0–4,0 раза, что повысит напряженное состояние кровли, а, следовательно, увеличит зону образования трещин.

Таким образом, в горных породах кровли при вышеуказанных варьируемых параметрах с граничными условиями защемление — свободная опора (закладка выработанного пространства), могут образовываться трещины в продольном и поперечном направлениях на некоторых участках. Во втором случае (полное обрушение) — на большей ее части во всех направлениях, т.е. с образованием хаотической трещиноватости.

Исследовано напряженное состояние кровли с двумя системами трещин, механические характеристики которой определялись по зависимостям (3)–(4), а средние значения d i=2? 10–2 м и D i=10–4 м. Результаты исследований показывают, что с увеличением мощности слоя напряженное состояние кровли снижается, причем оно ниже в кровле с хаотической трещиноватостью, что объясняется меньшими значениями механических характеристик по сравнению с системой зияющих трещин.

Разработанный метод расчета дает возможность определить напряженное состояние, целостность толщи горных пород с любым законом изменения жесткости, внешней нагрузки, параметрами в плане, расположением слоев с вышеуказанными граничными условиями. На основе получаемых результатов устанавливают места образования и ориентацию систем трещин, определяющих параметры образования пожароопасных зон. Результаты расчетов могут быть использованы для выбора способа локализации очагов самонагревания или горения.

 

Библиографический список

1. Костенко В.К. Теоретические основы расчета параметров пожароопасных полостей в выработанном пространстве выемочного поля // Горноспасательное дело. Сб. науч. тр. / НИИГД. — Донецк, 1998. — С.86–93.

2. Прочность. Устойчивость. Колебания. / Под общей ред. И.Я.Биргера и Я.Г.Пановко. — М.: Машиностроение. — 831 с.

3. Руппенейт К.В. Деформируемость массивов трещиноватых горных пород. — М.: Недра, 1975. — 222 с.

© Костенко В.К., 1999.