
| Тема работы: | "Исследование способов распределения вычислительной нагрузки при моделировании сетевого динамического объекта с распределенными параметрами" |
| Руководитель: |
профессор Святный Владимир Андреевич. |
| Консультант: | Молдованова Ольга Владимировна. |
| Выполнена в: | 2005 г. на кафедре "Вычислительной техники" "Донецкого национального технического университета" |
| Автоp: | Доста Максим Алексеевич. |
Опыт создания и эксплуатации параллельных машин говорит о том, что, как правило, переход от
однопроцессорной конфигурации к многопроцессорной системе из N процессоров не приводит
к сокращению времени вычислений в N раз.
Иными словами вычислительная мощность параллельной системы используется лишь частично и может возникнуть вопрос -
нужно ли задействовать подобную систему для решения задачи, если ее вычислительная эффективность в параллельном
режиме вычислений низкая?
Именно проблема распараллеливания программ является одной из важнейших проблем, возникающих в данный момент
перед разработчиком параллельного программного обеспечения.
Целью данной работы является исследование различных подходов к распределению задач между процессорами
с целью повышения быстродействия программы, а также применение этих способов распределения нагрузки
к сетевому динамическому объекту с распределенными параметрами.
Достижение поставленной задачи выполняется путем:
- исследования способов распределения нагрузки;
- исследования сложного динамического объекта с распределенными параметрами;
- исследования существующих объектно-ориентированных языков параллельного программирования и моделирования;
- разработка с учетом всех вышеперечисленных пунктов
объектно-ориентированной программы моделирования сетевого динамического объекта
с распределенными параметрами, с автоматическим распределением нагрузки.
Эта работа докладывалась на семинаре научно-исследовательских работ
на кафедре ЭВМ в апреле 2004 г.

|
| Рисунок 1. Переход от исходного графа топологии к графу задач |
Пусть граф G(V, Q), имеет n узлов и m ветвей, тогда аэродинамические процессы вызываются vent<=m вентиляторами и
r
Апроксимирую уравнения, которые описывают СДО по методу прямых, получают следующие уравнения для j - участка, i - ветви
(dx - шаг апроксимации) [8]
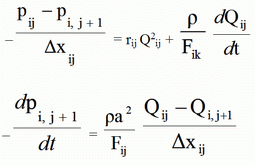
За счет того, что шаг аппроксимации по длине для каждой ветви одинаковый то можно сказать, что объем вычислений, будет прямо пропорционален длине ветви.
И исходя из этого, вес каждой вершины (Р) можно будет положить равным длине ветви исходного графа, которая разделена на шаг аппроксимации. Вес ветвей (М) можно взять равным единицы, так как между всеми процессами выполняется обмен данными одинакового размера.
Связь между вершинами графа Т отображает, между какими вершинами происходит обмен данными. Обмен данными выполняется на основании того, что некоторые процессы не вычисляют значение давления в конечных точках ветви, а используют эти значения принимая их от других процессов, которые занимаются вычислением ветви, которая тоже входит в этот узел (например процесс Р4 не вычисляет значение в точке 8, а принимает его из процесса Р3).
С другой стороны все процессы, которые описывают ветви, которые выходят из одной точки, должны получать давление в этой точке, вычисленное в процессе, который описывает ветвь, которая входит в эту точку (например давление в точке 2 из процесса Р1 передается к процессам Р2, Р5, Р6).
Также для вычисления давления в точке, в процесс, который вычисляет это значение, должны поступать начальные расходы из всех ветвей, которые выходят из этой точки и конечные расходы из тех, что входят (например, к процессу P3 должны поступать Q71, Q43).
Общий алгоритм формирования связей обмена данными можно сформулировать следующим образом (анализ структуры графа выполняется на основе матрицы инцидентности):
-количество узлов в графе алгоритма будет равно количеству ветвей в исходном графе;
-если есть узел в графе G, в который входят ветви, то считается, что давление в узле вычисляется при моделировании ветви с младшим индексом, которая в него входит. Всем остальным ветвям, которые входят и выходят из него это значение передается. Для вычисления давления необходимо к этой ветви передать все расходы воздуха на начальных участках для ветвей, которые выходят и конечные - для тех, что входят.
На рисунке 2 приведен пример перехода, где:
- Qi - исходные ветви;
- Pri - полученные из них процессы;
- Pkn1 - давление в точке kn1, которое расчитано в процессе Pri;
- Qik - расход воздуха в ветви і, в последнем аппроксимированном промежутке;
- Qin - расход воздуха в ветви і, в первом аппроксимированном промежутке.
Стрелками показано направление передачи данных.

Рисунок 2. Анимированный пример перехода от исходного графа к графу алгоритма с указанными направлениями передачи данных.
 отображается на какой-то путь
отображается на какой-то путь
 .
.
 M;f(v)<>f(w)}
будет количеством связей разбиения f, т.е. это суммарное количество всех ветвей графа, которые связывают вершины распределенные на разные ПЭ.
M;f(v)<>f(w)}
будет количеством связей разбиения f, т.е. это суммарное количество всех ветвей графа, которые связывают вершины распределенные на разные ПЭ.

|
| Рисунок 2. Схема работы многоуровневого алгоритма |

|
| Рисунок 3. Классификация алгоритмов разбиения графа |
В случае если целевая ЭВМ имеет статические линии связи, например Cray T3D (у которой коммуникационная сеть - трехмерный тор), Intel Paragon (коммуникационная сеть - двумерная прямоугольная решетка). То после этапа разбиения графа также требуется производить распределение кусков графа на ЭВМ потому как максимальный обмен данными должен производиться междй соседними элементами.
Для целевой ЭВМ строится матрица геометрии D, в которой находятся расстояния между соответствующими ПЭ. Расстояние между соседними ПЭ берется равным 1.
Тогда необходимо найти отображение, при котором обеспечивается экстремум целевой функции:

|
На текущий момент можно выделить 4 основные программы разбиения графа.
1. Библиотека METIS, разработанная в университете Миннесоты.
В данной программе используются многоуровневые алгоритмы разбиения графа. Существуют модификации данной программы для разбиения гиперграфов (HMETIS) и для параллельного разбиения графа (PARMETIS). PARMETIS использует библиотеку передачи сообщений MPI, и основывается на параллельных многоуровневых алгоритмах.
Функции данной библиотеки можно вызывать из программ, написанных на языках С и Fortran.
2. Библиотека SCOTCH, разработанная в университете г. Бордо [9].
В отличии от METIS данная библиотека предоставляет возможность не только разбивать граф, но и отображать его на целевую ЭВМ.
3 Библиотека JOSTLE, разработанная в университете г. Гринвич.
Эта библиотека предназначена для параллельного или последовательного разбиения графов.
4. PARTY - это библиотека, разработанная в Heinz Nixdorf институте и
университете г. Падерборн. Эта программа основывается на алгоритмах «бисекции» графа (деления пополам).

|

|
| Рисунок 5. Исходный граф. | Рисунок 6. Полученный граф алгоритма. |
Принцип построения системы передачи данных взят из концепции NUMA (Non Uniform Memory Access), представителем которых является BBN Butterfly [11]. Этот компьютер состоял из набора кластеров, которые соединялись через межкластерную шину. Каждый кластер соединял процессор, контроллер памяти, модуль памяти и некоторые устройства ввода/вывода. Когда процессору нужно было выполнить операции чтения или записи, он посылал запрос с необходимым адресом своему контроллеру памяти. Контроллер анализировал адрес, по которому и определял, в каком модуле содержаться необходимые данные. Если адрес локальный, то запрос выставлялся на локальную шину, в противном случае запрос отправлялся через межкластерную шину.
По подобному принципу и построена программа моделирования. На каждом процессорном элементе программно реализуется маршрутизатор. В него перед началом моделирования на основе исходных графов топологии и таблицы разбиения этого графа, записывается информация про то куда передавать данные.
Каждый объект, который моделируется в программе имеет свой интерфейс, при помощи которого объекты соединяются. В случае моделирования аэродинамического объекта каждый объект может получать расход воздуха или давление.
Таблицы маршрутизации заполняются уже во время начала моделирования, когда уже известно на каком процессорном находится тот или иной объект. Если объект хочет передать данные другому, который находится на этом же ПЭ, то данные записываются в локальную память по определенному адресу. В другом случае маршрутизатор посылает данные на другой ПЕ. Обмен данными выполняется при помощи механизма обмена сообщений MPI (Message Passing Interface) [14].

|
| Рисунок 7. Общая схема обмена данными. |
Синхронизация всех объектов выполняется по глобальному времени. Каждый из объектов моделирования имеет свой метод моделирования и локальный таймер. При моделировании каждый ПЭ увеличивает свой таймер на минимальный шаг моделирования и поочередно вызывает метод моделирования всех своих объектов. Каждый из объектов анализирует свой таймер, в котором записано время следующего подсчета значений, и если это значение больше чем глобальный таймер и к объекту не было послано никаких новых входных данных, то тогда не проводятся никакие вычисления. В другом случае выполняются вычисления и локальный таймер объекта увеличивается на шаг моделирования объекта.
Такой способ моделирования позволяет реализовать численные методы с плавающим шагом. Т.е. если есть группа объектов в которых значение не меняется на небольшом шаге моделирования, то можно увеличить шаг и тем самым уменьшить частоту вызова методов моделирования этих объектов.
После того как какой-то объект вычислил свое значение, то оно записывается в память, или сразу при помощи MPI функции Isend отсылается к другому объекту, расположенному на другом ПЭ (при передаче данных при помощи этой функции ПЕ, который передает данные не ждет пока другой ПЕ примет эти данные). Это позволяет равномерно распределить нагрузку сети при передаче данных.
После того, как закончилось моделирование всех объектов на этом шаге, увеличивается глобальный таймер, и вызываются функции Irecv, который получают отосланные ранее данные. После чего вызывается функция Barrier цель которой состоит в том, чтоб каждый ПЭ не выполнял следующие действия, пока хотя бы один з ПЭ не достигнет этой команды.
Общий алгоритм моделирования объектов представлен ниже.

|
| Рисунок 8. Общая блок схема алгоритма моделлирования. |
В этой работе было выполнено исследование способов распределение вычислительной нагрузки для параллельных систем. Также на основе предыдущего опыта моделирования СДО, создания языков моделирования, создания языков параллельного моделирования и основных архитектур параллельных ЭВМ было создана объектно-ориентированная программа моделирования СДО с распределенными параметрами с автоматической балансировкой нагрузки.
Далее планируется исследование эффективности распределения нагрузки для СДО на разных архитектурах и с использованием разных алгоритмов разбиения графа. Также будет реализована динамическая балансировка нагрузки с целью возможности использования численных методов с переменным шагом, и возможности во время работы программы создавать новые объекты моделирования или удалять старые (т.е. менять структуру входного графа, описывающего топологию сети).