Надежность и контроль качества. - 1997. - № 5. - С. 26-35.

УДК 519.2

 

Группирование наблюдений как способ получения робастных оценок

 

Лемешко Б.Ю.

 

Опираясь на вид функции влияния Хэмпеля и результаты экспериментов, утверждается, что оценки максимального правдоподобия по группированным дан­ным, в отличие от оценок по негруп­пированным данным, являются робастными.

 

            Цель данной работы еще раз обратить внимание прикладных ста­тистиков на вопросы надежности статистических выводов, в част­ности, на робастность оценок параметров законов распределений, и настоятельно рекомендовать один из подходов к получению робастных оценок.

            В статистике под робастностью понимают нечувствительность к малым отклонениям от предположений [1].

            Какие же отклонения от предположений влияют на оценки? Допус­тим, что наблюдаемая выборка действительно принадлежит тому закону распределения, оценки которого мы пытаемся найти. В этом случае от­клонения могут быть связаны с наличием аномальных наблюдений, появ­ление которых в выборке определяется самыми различными при­чинами. Если не учитывать наличие аномальных наблюдений, попытки оценивания параметров распределения могут привести к самым плачевным резуль­татам. Что же делать? Естественно, надо отбраковать аномальные изме­рения, а затем искать оценки параметров. К сожалению реализовать от­браковку наблюдений в общем случае оказывается совсем не просто. Наблюдения, аномальные с позиций одного закона распределения, явля­ются естественным проявлением закономерностей второго. Если нет на­дежной процедуры отбраковки или практических соображений, связанных с физикой наблюдаемой величины, пытаются выйти из по­ло­жения одним из следующих способов. В первом случае усекают выборку, отбрасывая определенную часть минимальных и/или максимальных на­блюдений, и по оставшейся части оценивают параметры распределения. Во втором - перед процедурой оценивания вин­зорируют выборку: всем наблюдениям левее и/или правее определенных значений присваивают одинаковые значения. Обе эти процедуры далеко не всегда приводят к положительным резуль­татам. Кроме того в обоих случаях мы имеем дело с новой гене­раль­ной совокупностью, которой принадлежит видоизмененная выборка. Более пра­вильным следует считать третий подход, когда выборку цензурируют. Для наблюдений, попавших левее и/или правее опреде­ленных значений, фик­сируют лишь факт попадания в соответствующий интервал, опуская кон­кретные значения этих наблюдений. По такой цензу­рированной вы­борке оценивают параметры закона.

            Другая ситуация. В выборке нет аномальных наблюдений, но наблю­даемый закон распределения отличается от предполагаемого. Такая ситу­ация наиболее реальна, так как множество законов рас­пределения вероят­ностей бесконечно, а количество моделей, используемых на практике для описания наблюдаемых случайных величин, очень огра­ничено. Чем сущес­твенней вид предполагаемой модели отличается от реально наблюдаемого закона, тем сильнее это отражается на оценках параметров.

            Очевидно, что в наблюдаемых на практике выборках и за­кон, пусть мало, но отличается от используемой модели, и обычно налицо аномальные наблюдения. Поэтому при­ме­нение цензурирования, одно­сторонннего или двустороннего, редко приносит желаемый эффект.

            Одним из наиболее популярных и эффективных методов оценивания параметров распределений является метод максимального правдоподобия. Достаточно часто приходится сталкиваться с необоснованными утвер­жде­ниями, что оцен­ки максимального правдоподобия (ОМП) являются ро­бастными и, именно поэтому, предпочтительно использовать именно их. Автор является го­рячим сторонником метода максимального правдо­подо­бия, но вместе с тем, основываясь на достаточно большом практическом опыте и некоторых результатах, обязан подчеркнуть, возможно очевидное для многих, что в общем случае ОМП параметров распределений не являются робастными.

            Проиллюстрируем сказанное следующими примерами. Это мож­но бы­ло бы сделать с одинаковым эффектом на различных законах рас­пре­деления, но, учитывая роль нормального распределения в теории и при­ложениях математической статистики, приведем примеры именно с нор­мальным законом. Приводя эти примеры, мы не преследуем цель показать какие плохие оценки полу­чаются, а пытаемся убедить, что из этих си­туаций возможен выход, дающий надежные результаты. В первом примере иллюстрируется влияние аномальных ошибок на ОМП параметров нор­мального распре­де­ления, а во втором параметры нормального закона оце­ниваются по вы­борке, принадлежащей другому закону распределения. Для чистоты экспе­римента выборки моделируются в соответствии с заданными законами.

Пример 1.           Выборка по нор­мальному закону моделировалась с матема­тическим ожиданием  и среднеквад­рати­чес­ким отклонением . На рис. 1 приведены результаты статистического анализа смоделированной выборки. Вычисленные значения ОМП  и . На этом и последующем аналогичных рисунках приведены значения статистик отношения правдоподобия,  Пирсона, Колмогорова, Смирнова,  и  Мизеса, вычисляемые при проверке гипотез о согласии, и соответ­ствующие вероятности вида , где  - вычисленное значение соответствующей статистики,  - предельное распределение вероятностей для статистики. Гипотеза о согласии не отвергается, если , где  - заданный уровень значимости. Для ста­тистик отношения правдоподобия и  Пирсона значения вероятностей при­во­дятся при двух различных степенях свободы. Разность степеней свободы определяется количеством параметров, оцененных по выборке. При вычис­лении вероятностей вида  для непараметрических критериев ти­па Колмогорова, Смирнова,  и  Мизеса учитывается факт потери ими свойства “свободы от распределения” [2]. Как видим, согласие с нор­мальным законом очень хорошее.

            Теперь допустим, что в выборку “вкралось” всего 3 аномальных наблю­дения (в результате замены трех первых наблюдений:  на ,  на ,  на ). Результаты ана­лиза с теоретической и эмпиричеcкой функциями распределения приведены на рис. 2. Полученные ОМП параметров нормального распределения  и . Особенно существенно наличие аномальных наблюдений повлияло на оценку среднеквадратичного отклонения. По всем критериям согласие с нормальным законом распределения будет отклонено при уровне значимости  > 0.0008.

Пример 2. Этот пример связан с использованием нормального закона распределения в ситуации, когда на самом деле выборка принадлежит распределению Лапласа. Это распределение с более “тяже­лыми” хвостами, чем у нормального. На рис. 3 приведены эмпирическая и теоре­тические функ­ция нормаль­ного распределения, когда по выборке, смоделированной в соответствии с распределением Лапласа, оценивались параметры нор­маль­ного закона (). Как видно из значений статистик и соответствующих вероятностей, ни о какой близости эмпирической и теоретической функций распределения говорить не приходится.

 

 

Рис.1. Результаты статистического анализа исходной выборки по негруппированным данным

 

Рис.2. Эмпирическая функция распределения (1) и теоретическая функции нормального распределения (2), полученная по выборке с аномальными наблюдениями

 

            Естественно, что использование получившихся в этих 2-х примерах нормальных законов в качестве моделей наблюдаемых выборок ни к чему хорошему не приведет.

 

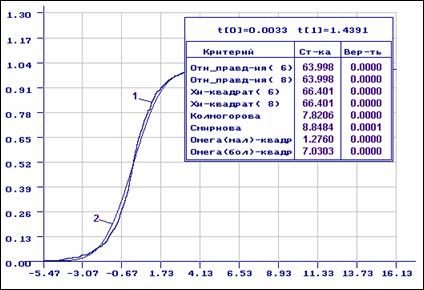
Рис.3. Эмпирическая функция распределения (1) и функция распределения нормального закона (2), найденного по выборке, принадлежащей распределению Лапласа

 

            Что же можно сделать, чтобы снизить влияние аномальных ошибок и отклонений наблюдаемых выборок от предполагаемого закона на оценки вычисляемых параметров? Мы настоятельно рекомендуем использовать пе­ред вычислением оценок параметров процедуру предварительного группи­рования наблюдений. Группирование выборки позволяет резко снизить влияние аномальных наблюдений, а иногда практически исключить по­следствия присутствия их в выборке. Резко снижается влияние на оцен­ки параметров и отклонений вида наблюдаемого закона от предпо­лагаемого. Продемонстрируем это на выборках приведенных примеров.

            На рис. 4 представлены результаты оценивания параметров нор­маль­ного распределения и последующего анализа по сгруппированной вы­борке из примера 1, содержащей 3 аномальных наблюдения (сравните зна­чения статистик и соответствующих вероятностей с представленными на рис. 2). Полученные ОМП параметров нормального распределения по группи­ро­ванным данным  и . Визуального раз­личия меж­ду эмпирической и теоретической функ­цией нормального закона в данном случае нет, поэтому соответ­ствующие графики не при­водятся.

Рис. 4. Результаты оценивания по сгруппированной выборке и последующего статистического анализа при наличии в выборке аномальных измерений

 

            На рис. 5 представлены результаты оценивания по сгруппированным данным параметров нор­мального закона по вы­борке из примера 2, при­надлежащей распределению Лапласа (сравните результаты анализа с ре­зультатами, представленными на рис. 3). ОМП параметров нормального рас­пределения по группированным данным  и . В данном случае в центре области определения случайной величины наблю­дается некоторая близость эмпирической функции распределения и функ­ции распределения нор­маль­ного закона.

            В работах [3-5] подчеркивается высокая устойчивость оценок мак­си­мального правдоподобия по группированным наблюдениям к нали­чию в выборке аномальных измерений, к отклонению реально наблю­даемого за­кона от предполагаемого, к засорению выборки данными, при­надлежащими другому закону. Это подтверждается опытом эксплу­атации программной системы [3] и многочисленными результатами модель­ных экспериментов. В работе [6] свойство робастности ОМП исследовано с позиций функции влияния, предложенной Хэмпелом [7]. Анализ функций влияния ОМП параметров для множества законов распределения, включенных в про­грам­мную систему [3] (26 непрерыв­ных законов рас­пределения слу­чайных ве­личин, наиболее часто исполь­зуемых в при­ложениях), позволил утвер­ждать, что ОМП по негруп­пи­рованным данным, вопреки порой бытую­щему заблуждению, в боль­шинстве своём являются неробастными. В то же время ОМП по груп­пированным данным всегда ро­баст­ны.

 

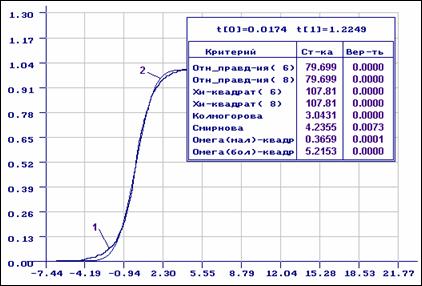
Рис. 5. Эмпирическая функция, построенная по выборке, принадлежащей распределению Лапласа (1), и теоретическая функция нормального закона (2), найденная по сгруппированной выборке

 

            Влияние ещё одного наблюдения на очень большую выборку может характеризоваться функцией (кривой) влияния, которая опре­де­ляется сле­ду­ющим образом [1]

,

где  - единичная масса в точке ,  - функция распределения, к кото­рому принадлежит выборка,  - вычисляемая статистика. Эта функция позволяет оценить относительное влияние от­дель­ного наблюдения на зна­чение статистики критерия или оценку параметров. Если функция влияния неограничена, то резко выделяющиеся наблюдения могут при­водить к сущес­твенным изменениям оценок или статистик.

            Для асимптотически эффективных оценок, к которым относятся оцен­­ки максимального правдоподобия по негруппированным дан­ным, функ­ция влияния удовлетворяет ра­венству [1]

,

где  - количество информации Фишера,  - оцениваемый параметр закона распределения.

            В работе [6] были исследованы функции влияния для ОМП пара­метров по негруппированным данным всех 26 зако­нов, включенных в программную систему [3]. И все они (за исключением функций влияния для оценок параметров распределения Коши и параметра сдвига логисти­ческого распределения) представляют собой неограниченные функции на области опре­деления соответствующих случайных величин. А вот функции влияния для ОМП по груп­пированным данным всегда представляют собой ограниченные по величине ступенчатые зависимости.

            Приводимые на рис. 6-7 в качестве примера функции влияния для оценок параметров рас­пре­деления Вейбулла построены при конкретных зна­­чениях параметров и характеризуют качественную картину их поведения на об­ласти определения случайных величин. Вид функций влияния говорит о чувствительности к аномальным ошиб­кам и засорению выборки ОМП по негруппи­рован­ным данным, и об устойчивости ОМП по группи­рован­ным.

 

Рис.6. Функции влияния для основного (формы) параметра

распределения Вейбулла по негруппированным и

сгруппированным данным (ступенчатая линия)

 

            Подведем итоги вышесказанному. Группи­рование наблюдений перед оцениванием и последующее оценивание параметров по группи­рованной выборке позволяет получать устойчивые оценки. Когда мы говорим об оценках по группированным данным, то имеем ввиду ОМП, которые определяются в результате максимизации функции правдоподобия вида

,

где  - вероятность попа­дания на­­блю­дения в -й интер­вал значений, k - число интервалов, но только не оценки по методу моментов с последующим использованием поправок типа Шеп­парда.

 

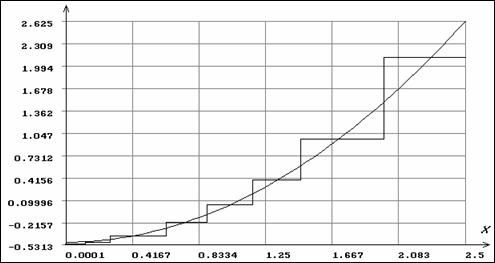
Рис. 7. Функции влияния для параметра масштаба распределения Вейбулла по негруппированным и сгруппированным данным (ступенчатая линия)

 

            Естественно, мы предлагаем использовать оценки по группированным данным не вместо, а вместе с оценками по негруппированным наблю­де­ниям. Качество тех и других зависит от степени засоренности выборки ано­мальными наблюдениями или близости к предполагаемому закону рас­пределения.

            При группировании наблюдений мы несём потери информации о параметрах закона распределения, в том числе потери в информационном количестве Фишера [8-9], с которым связана асимптотическая дисперсия асимптотически эффективных оценок, в частности ОМП. Асимптотическая дисперсия ОМП по группированным данным определяется соотношением

,

 - количество информации Фишера о параметре  в одном груп­пи­рованном на­блюдении,  - объем выборки. Больше потери - больше асимпто­ти­чес­кая дисперсия оценки. Подчеркиваем, асимптотическая дис­пер­сия. Реально же, при наличии в выборке неоднократно упоминаемых отклонений, дис­персия оценок по группированным данным оказывается меньше, чем по негруп­пированным. Т.е. вклад в дисперсию от потерь в асимптотике ока­зывается несоизмеримо мал по сравнению с вкладом, свя­занным с нали­чием отклонений.

            Остаётся вопрос, как группировать? Можно различным образом. Не стоит, конечно, рассматривать крайние случаи: сгруппировать можно и так, что в группированной выборке не останется никакой информации о законе и его параметрах. Реально на интервалы разбивают область, определяемую размахом выборки. Это могут быть или интервалы равной длины, или ин­тервалы равной вероятности (равной частоты), или асимптотически опти­мальные интервалы [9] (минимизирующие потери от группирования в ин­формационном количестве Фишера о параметрах закона распределения), или интервалы, сформированные по какому-то другому принципу. Обычно наиболее устойчивыми к отклонениям ока­зы­ваются оценки при разбиении выборки на интервалы равной вероятности. В то же время в случае асимп­тотически оптимального группирования потери информации о пара­метрах закона распределения, связанные с группированием, существенно меньше, чем при равновероятном. Если мы знаем, что отклонения от наших пред­положений в выборке минимальны, то использование таблиц асимпто­ти­чески оптимального группирования, широко представленных в [9], по­зво­ляет резко сократить объемы храни­мых данных без сущес­т­вен­ной потери информации о законе распределения. Но всё-таки в общем случае здесь следует ожи­дать большей чувствительности оценок к откло­не­ниям от предпо­ло­жений.

            С другой стороны достаточно часто мешающая информация, связан­ная с за­сорением выборки, оказывает меньшее влияние на оценки, чем потери ин­формации от группирования при асимп­тотически оптимальном группиро­вании. В некоторых случаях оценки с использованием асимп­то­тически оптимального группирования оказываются так же устойчивыми, как и при равно­веро­ят­ном, и при этом показывают лучшие результаты. Поэтому рекомендуется вы­числять две оценки по группированным данным с использованием как оптимального, так и равновероятного группирования, и остановиться на той оценке, которая дает лучшее согласие с исходной выборкой [5].

 

1.      Хьюбер П. Робастность в статистике. - М.: Мир, 1984. - 303 с.

2.      Лемешко Б.Ю., Постовалов С.Н. К вопросу о распределениях ста­тистик непараметрических критериев согласия // Сб. научных тру­дов НГТУ. - 1997. - №1. (в печати).

3.      Лемешко Б.Ю. Статистический анализ одномерных наблюдений слу­чай­ных величин: Программная система. - Новоси­бирск: Изд-во НГТУ. - 1995. - 125 с.

4.      Лемешко Б.Ю., Постовалов С.Н. Статистический анализ одномерных наблюдений по частично группированным данным // Изв. вузов. Фи­зика. -  Томск, 1995. - № 9. - С. 39-45.

5.      Лемешко Б.Ю., Постовалов С.Н. Вопросы обработки выборок од­но­мерных случайных величин // Научный вестник НГТУ, 1996. - № 2. - C.3-25.

6.      Лемешко Б.Ю., Постовалов С.Н. К вопросу о робастности оценок по группированным данным // Сб. научных тру­дов НГТУ. - 1996. - №2. (в печати).

7.      Hampel F.R. The influence curve and its role in robust estimation // J. Amer. Statist. Ass., 1974. - V. 69, № 346. - P. 383-393.

8.      Куллдорф Г. Введение в теорию оценивания по группированным и час­тично группированным выборкам. - М.: Наука, 1966. - 176 с.

9.      Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное груп­пи­рование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. - 346 с.