Заводская лаборатория. - 1997. - Т.63. - № 5. - С. 43-49.

УДК 519.24

Робастные методы оценивания и отбраковка аномальных измерений

Б.Ю. Лемешко

            При решении задач статистического анализа и, в частности, при вычислении оценок параметров распределений проблема наличия в выборке аномальных измерений имеет чрезвычайно важное зна­чение. Присутствие единственного аномаль­ного наблюдения может приводить к оценкам, которые совер­шен­но не согласуются с выборочными данными.

            В борьбе с грубыми погрешностями измерений, если они не были обнаружены в процессе измерений, используют два подхода:

·        исключение резко выделяющихся аномальных измерений из даль­ней­шей обработки;

·        использование робастных методов обработки.

            В данной работе остановимся на комплексе взаимосвязанных вопро­сов: “простом” способе робастного оценивания параметров непрерыв­ных законов распределения, мощности критериев согласия и достаточно эффек­тивном параметрическом методе отбраковки аномальных наблюдений.

            В статистике под робастностью понимают нечувствительность к малым отклонениям от предположений [1].

            Понятно желание каждого исследователя, чтобы найденные оцен­ки были как можно менее чувствительны к аномальным наблюдениям. В противном случае прежде чем переходить к оцениванию, приходится использовать процедуры исключения грубых ошибок изме­ре­ний, что выливается в непростую задачу, которая, как справедливо отмечается в [2], без устойчивых методов надёжно не реша­ет­ся. Соглашаясь в принципе со справедливыми доводами, приводимыми в этой работе в поддержку вывода о неустойчивости пара­метрических методов отбраковки резко выделяющихся наблюдений, мы не склонны хоронить параметрические методы, так как при опре­де­лённых условиях получаются очень хорошие результаты.

            Воспользуемся почти дословно постановкой задачи отбраковки, как она изложена в [2]. Рассматривается ситуация, когда  числа. Резко выделяется одно наблюдение, для определен­ности . При нуле­вой гипотезе  наблюдения  рассмат­риваются как реализация независимых одинаково распределенных случай­ных величин  с функцией распределения . При аль­тернативной гипотезе  случай­ные величины  также неза­висимы,  имеют распределение , а  - распре­деле­ние , которое “существенно сдвинуто вправо” относительно , например , где  достаточно велико. Если , то прини­мается гипотеза , в противном случае - гипотеза . При спра­вед­ливости нулевой гипотезы , и кри­ти­чес­кое значение  опре­деляется из уравнения . При боль­ших  и малых  

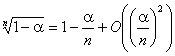,                         (1)

поэтому в качес­тве хорошего приближения к  рассматривают _-квантиль рас­пре­де­ления .

            Неустойчивость такой процедуры отбраковки в работе [2] связана с возможным неточным определением закона  и труд­ностью различения близких законов распределения с помощью критериев согласия и, в част­ности, с помощью критерия Колмогорова. Приводимые доводы спра­вед­ливы. Те исследователи, кто неоднократно в своей практике пытал­ся иден­тифи­цировать закон распределения, связанный с кон­кретной выбор­кой, убе­дил­ся, что достаточно часто используемый критерий согласия не даёт оснований отвергать целый ряд законов распре­деления. Способность кри­те­рия различать близкие альтернативные гипотезы определяется его мощ­ностью. Именно недостаточная мощность критерия не позволяет нам принять решение.

            Приводимые далее примеры и выводы получены на основании результатов, которые были использованы при создании про­граммной системы [3], разработанной в Новосибирском государственном техничес­ком универси­тете, и опыте её применения.

            В программной системе все задачи статистического анализа данных рассматриваются с точки зрения наиболее общего представления экспери­мен­таль­ных наблюдений в виде частично группированных выборок [4,5], частными случаями которых являются негруппированные, группиро­ванные и цензурированные выборки. Выборка яв­ля­ется негруп­пи­ро­ван­ной, если выбо­роч­ные значения представляют собой индивиду­альные зна­че­­ния на­блю­де­ний из области определения случайной величи­ны. Выборка является группированной, если область оп­ре­­­деления случай­ной величины разбита на  непересе­кающихся интервалов гранич­ными точками

,

где  - нижняя грань области определения случайной ве­ли­чины X,  - верхняя грань области определения случайной величины X, и зафикси­рованы количества наблюдений , попавших в _-й интервал значений. Выборка является частично группированной, если име­ющаяся в нашем распоряжении информация связана с мно­жеством непересекающихся интер­валов, которые делят об­ласть определения случайной величины так, что каждый ин­тер­вал принадлежит к одному из двух типов:

а) _-й интервал принадлежит к первому типу, если число  известно, но индивидуальные значения , неиз­вестны;

б) _-й интервал принадлежит ко второму типу, если известно не только число , но и все индивидуальные значения .

Область определения случайной величины в этом случае можно представить в виде , где  - множество интервалов первого типа, а - множество интервалов второго типа.

            Совокупность решаемых задач позво­ляет идентифицировать закон распределения случайной величины. Иден­ти­фикация закона распределения происходит по следующему алгоритму: ограничение множества “подхо­дящих” распределений; определение для каждого закона распределения из данного множества оценок неизвестных парамет­ров и проверка гипотез о согласии полученного закона распределения с исход­ными данными; выбор того закона распределения, согласие с которым наиболее хорошее.

            Программная система охватывает класс, состоящий из 26 непрерыв­ных законов распределения случайных величин, наиболее часто исполь­зуемых в приложениях: экспоненциального, полунор­мального, Рэлея, Макс­велла, мо­дуля многомерного нор­мального век­тора, Парето, Эрланга, Лапласа, нор­мального, логарифмически ­нормальных (ln и lg), Коши, Вейбулла, Нака­гами, распределения ми­нимального значения, распределе­ния макси­маль­ного значения, двой­ного показательного, гамма-распределения, логистического, бета-­распределения 1-го рода, стандартного бета-рас­пре­деления 2-го рода, бета-распределения 2-го рода, распреде­лений -Джон­сона, -Джонсона и _-Джонсона, экспоненциального семейства рас­пределений.

            Основным методом оценивания параметров распределений, заложен­ным в системе, является метод максимального правдоподобия. Оценки параметров распределений находятся в результате максимизации функции прав­­­­до­подобия по частично группированной выборке, которая имеет вид:

,

где  - функция плотности случайной величины, 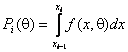 - вероятность попа­дания на­­блю­дения в _-й интервал значений, (1) и (2) озна­чают, что умножение осуществляется по интер­валам с группирован­ными и негруппированными данными соответственно.

            Проверка гипотез о согласии осуществляется по ряду критери­ев: отно­шения правдо­по­добия,  Пирсона, Колмогорова, Смирнова,  и  Мизеса. Реше­ние о степени соответствия выборки с законом распреде­ления принимается по их совокупности.

            При проверке гипотез о согласии проверяется гипотеза вида  . В принятой практике статистического анализа проверка как правило осуществляется по следующей схеме. Для выбранного крите­рия вычисляется значение  статистики  как неко­то­рой функции от выборки и закона распределения . Для исполь­зуе­мых на практике критериев обычно известны асимптотические распределе­ния  соответ­ствующих статистик при условии истинности ги­потезы . Далее сравни­ва­ют полученное значение статистики  с критическим для данного уров­ня значимости  и нулевую гипотезу отвергают, если . Крити­ческое значение , определяемое из уравнения

,

где  - задаваемый уровень значимости, обычно берётся из соответ­ствующей статистической таблицы.

            В такой ситуации остается за кадром величина вероятности превы­шения полученного значения статистики при истинности нулевой гипотезы, хотя именно она и позволяет судить о степени согласия, так как по сущес­тву представляет собой вероятность истинности нулевой гипотезы.

            Для включенных в программное обеспечение критериев в обяза­тельном порядке отображается соответ­ствующая вероятность превышения полученного значения статистики при истинности нулевой гипотезы

.

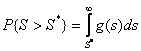Гипотеза о согласии не отвергается, если .

Статистика критерия согласия  Пирсона при истинной гипотезе  в пределе подчиняется _-распределению с числом степеней свободы , если по выборке не оце­нивались пара­метры, и с , если по ней оценивалось  параметров закона распре­деления. Вероятность вида  для распреде­ления  вычисляется при числе степеней свободы  и . Все вышесказанное справедливо и для критерия отношения правдоподобия [6].

            Для непараметрических критериев Колмогорова, Смирнова,  и  Мизеса предельные распределения статистик известны только для ситу­ации полностью определенных законов распределения  [7]. К сожа­ле­нию, в случае оценивания параметров по выборке и даль­ней­шей проверки согласия с соответствующим законом действительные пре­дельные распре­деления непараметрических критериев существенно отли­ча­ются [8]. Использование же предельных распределений, соответствующих гипотезе  с известными параметрами, приводит к неоправдано завышенным зна­чениям вероятностей вида , что прослеживается и на приво­димых ниже примерах.

            В данной работе отметим два достоинства методов, реализованных в программной системе. Во-первых, свойства получаемых оценок, исполь­зующих группирование исходных выборочных данных. Очевидно, что они менее чувствительны к случайным выбросам. Группирование выборки позволяет резко снизить влияние аномальных наблюдений, а иногда и практически исключить влияние грубых ошибок измерений. Во-вторых, использование асимптотически оптималь­ного группирования в критериях отно­шения правдо­по­добия и  Пирсона [5]. Мощности крите­риев отно­шения правдо­по­добия и  Пирсона про­порциональны количес­тву инфор­мации Фишера о параметрах распре­деле­ния в группированной выборке. Асимптотически оптимальное группирова­ние минимизирует поте­ри инфор­мации, связанные с группированием и следовательно гарантирует макси­мальную мощность различения близких альтернатив для этих крите­риев. Полученные ранее таблицы асимптоти­чески оптимального груп­пи­рования [5] встроены в программное обеспе­чение.

            В задаче отбраковки аномальных наблюдений на разных этапах её решения к статистическим процедурам оценивания и проверки гипотез предъявляются, вообще говоря, прямо противоположные требования. На этапе идентификации закона распределения и оценивании его параметров методы должны быть как можно менее чувствительны к наличию ано­мальных ошибок измерений. Наоборот, на последующем этапе исключения аномальных измерений критерий должен улавливать их наличие и позволять отсекать.

            Таким образом, при идентификации (при оценивании параметров распределений) мы должны использовать робастные алгоритмы (устой­чивые к наличию аномальных наблюдений), а на последующем этапе отбраковки желательна максимальная мощность критерия для различения близких альтернатив (чувствительность к грубым ошибкам). В этой связи мы реко­мендуем на первом этапе использовать оценки по группированным данным, причем для большей устойчивости оценок осуществлять разбиение выборки на интервалы равной вероятности (равночастотные интервалы), а на втором этапе при проверке согласия - разбиение на асимптотически оптимальные интервалы.

            Продемонстрируем сказанное на конкретном примере. Была смодели­рована выборка объёмом 1000 наблюдений в соответствии с распределе­нием Вейбулла с плотностью

.

При моделировании были заданы параметры:  В процессе регистрации 8 наблюдений “подверглись” сильным искажениям.

            На рис.1-2 приведены результаты статистического анализа полу­ченной выборки. Здесь и в дальнейшем . На рисунках отражаются результаты проверки гипотез о согласии: вычис­ленные значения  соответствующих статистик  и вероятности пре­вы­­шения полученного значения статистики при истинности нулевой гипоте­зы . Гипотеза о согласии не отвергается, если . В данном случае получили закон распределения Вейбулла с параметрами  Как видим из рис.1, согласие по всем критериям отвергается: наличие аномальных наблюдений сыграло свою роль. На рис.2 хорошо заметна разница между эмпирической и теорети­ческой функциями распределения.

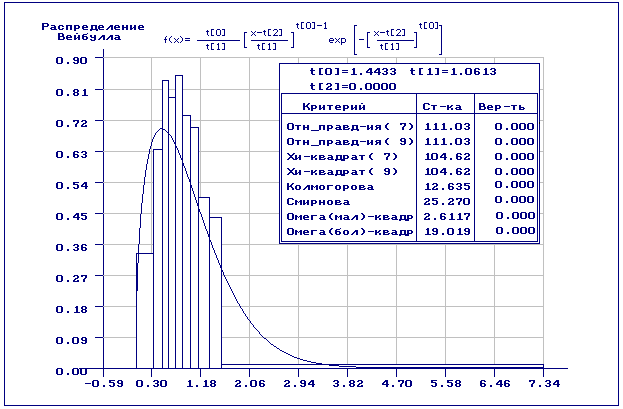
Рис.1. Результаты статистического анализа исходной выборки по негруппированным данным

Рис.2. Теоретическая и эмпирическая функции распределения

            На рис.3 приведены результаты статистического анализа, когда перед оцениванием выборка была разбита на интервалы равной частоты, затем по получившейся группированной выборке были найдены оценки пара­метров распределения , после чего прове­рены гипотезы о согласии исходной выборки с полученным законом распределения. При проверке гипотез о согласии исходная выборка разбивалась на интервалы равной вероятности. Как видим, результаты проверки гипотез о согласии по всем критериям очень хорошие.

Рис.3. Оценивание с предварительным равночастотным груп­пированием и проверкой гипотез о согласии с разбиением на равночастотные интервалы.

            Отличие результатов на рис. 4 определяется тем, что при проверке гипотез о согласии исходная выборка разбивалась на интервалы в соот­ветствии с асимптотически оптимальным группированием. В данном случае критерии отношения правдоподобия и  Пирсона оказываются более чувствительными, чем остальные, улавливают наличие аномальных измерений. Гипотезы о согласии при  по этим критериям должны быть отвергнуты.

            Приведенные на рис.5-6 результаты анализа, анало­гичны тем, что представлены на рис.3-4, но перед оцениванием выборка была разбита на асимптотически оптимальные интервалы. Получены оценки пара­метров . Если при проверке гипотез исходная выборка разбивалась на интервалы равной вероятности (рис. 5), то гипотеза о согласии по всем критериям прини­мается. При использовании асимптотически оптимального группирования гипотеза о со­гласии по критериям отношения правдоподобия и  Пирсона должна быть отверг­нута (рис.6). Если мы сравним эти результаты, с резуль­татами, представ­ленными на рис. 3-4, то увидим, что уровень согласия в данном случае ниже. То есть, полученные оценки оказались хуже, а способ их опре­деления более чувствителен к аномальным наблюдениям.

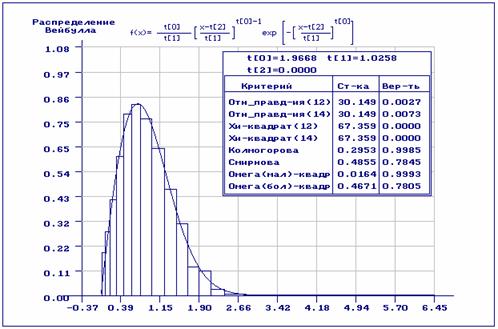
Рис.4. Оценивание с предварительным равночастотным груп­пированием и проверкой гипотез о согласии с разбиением на асимптотически оптимальные интервалы

            Для отбраковки аномальных наблюдений зададимся уровнем значи­мос­ти  и, опираясь на соотношение (1), при объёме выборки  и векторе параметров  распределения Вейбулла найдем  (в систему встроена возмож­ность вычисления различных вероятностей для законов распределения). Далее, мы должны исключить те наблюдения, которые превышают величину . Таких наблюдений оказалось 8.

            На рис.7 отражены результаты статистического анализа выборки после исключения из неё аномальных наблюдений. При проверке согласия использовано разбиение области определения случайной величины на равновероятные интервалы. Как видим, согласие по всем критериям очень хорошее. На рис.8 представлены аналогичные результаты с использо­ванием асимптотически оптимального группирования в критериях согласия.

            В довершение картины на рис.9 приведены результаты проверки согласия найденного закона (после отбраковки грубых ошибок измерений) с исходной выборкой, содержащей ошибки измерений, с применением асимптотически оптимального группирования.

            Нельзя не привести ещё один пример, подчеркивающий устойчивость оценок максимального правдоподобия по группированным данным. Он связан с использованием нормального закона распределения в ситуации, когда на самом деле выборка принадлежит распределению Коши.

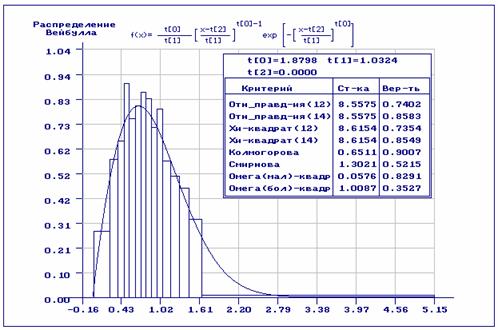
Рис.5. Оценивание с предварительным асимптотически опти­мальным группированием. При проверке согласия использо­ваны равночастотные интервалы.

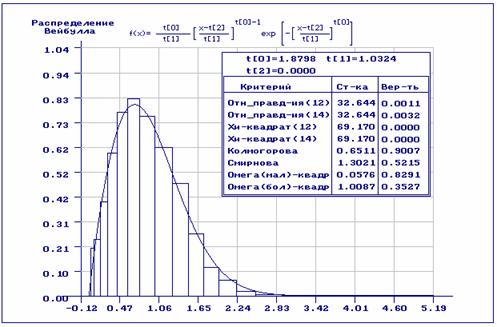
Рис.6. Оценивание с предварительным группированием с разбиением на асимптотически оптимальные интервалы. При проверке согласия также использовано асимптотически  оптимальное группирование.

Рис.7. Результаты анализа после удаления аномальных на­блю­дений (при проверке согласия использовано равночас­тотное группирование)

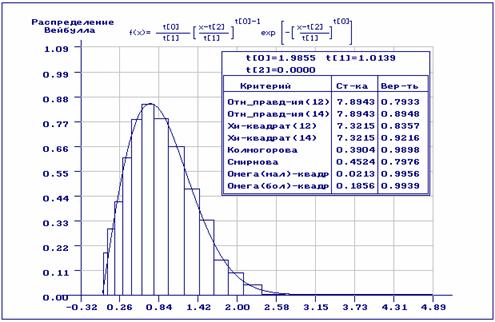
Рис.8. Результаты анализа после удаления аномальных на­блюдений (при проверке согласия использовано асимптоти­чески оптимальное группирование)

            Распределение Коши это распреде­ление с “тяжелыми” хвостами, а такое отклонение от нормаль­ности особенно сильно отражается на оценках параметров нормаль­ного закона. На рис. 10-11 приведены эмпирическая и теоре­тические функ­ции нормаль­ного распределения при использовании обычных оценок мак­си­мального правдоподобия (рис.10, оценки параметров нормального рас­пределения: ) и оценок макси­мального правдо­по­до­бия по группированным данным (рис.11, оценки: , ). Качес­­твенная картина, хорошо прослеживаемая на графиках, говорит сама за себя: во втором случае можно даже говорить об определенной близости эмпирической и теоретической функций распре­деления. Выборка объё­мом 100 наблюдений моделировалась по закону Коши с функцией плотности  и параметрами , .

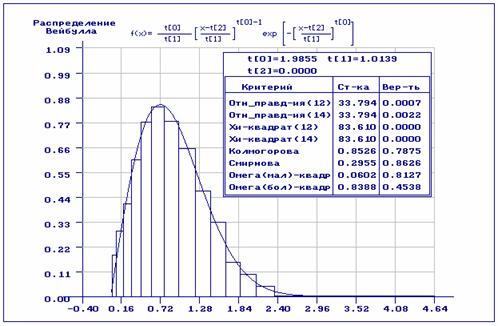
Рис. 9. Проверка согласия с исходной выборкой (при проверке согласия использовано асимптотически опти­маль­ное груп­пирование)

Выводы

1.      При решении задачи отбраковки на этапе идентификации закона распределения (при оценивании параметров распределений) следует использовать робастные алгоритмы (устой­чивые к наличию аномальных наблюдений). Высокую устойчивость к присутствию в выборке грубых искажений или принадлежности выборки к другому закону распреде­ления проявляют оценки максимального правдоподобия по группирован­ной выборке. Обычно наиболее устойчивы эти оценки при разбиении области определения случайной величины на интервалы равной веро­ятности (равночастотные интервалы). Однако достаточно часто устой­чивее оказываются оценки, использующие асимптотически оптимальное группирование. Поэтому целесообразно рекомендовать на этом этапе оба способа группировки при вычислении оценок с последующим выбо­ром тех, которые дают наилучшее согласие.

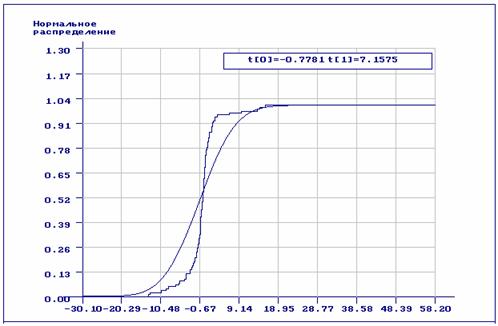
Рис.10. Эмпирическая функция распределения и нормальный закон распре­деления, найденный по выборке, принадлежащей распределению Коши.

2. В общем случае критерии согласия являются недостаточно мощными, чтобы распознать близкие альтернативы (близкие законы распреде­ления). Этим определяется, что достаточно часто используемые кри­терии не позволяют отклонить гипотезу о согласии с одним распреде­лением, с другим, с третьим ... Нельзя доверять выводам типа “с уров­нем значимости таким-то гипотеза о согласии с нормальным распре­делением не отвергается”, так как наверняка с большим осно­ванием не будет отвер­гаться гипотеза о согласии и с другими распреде­лениями. Если нас действи­тельно интересует, насколько сильно отлича­ется выборка от предполагаемого распределения, следует применять кри­тери­и отно­шения правдо­по­добия и  Пирсона с использованием асимптоти­чески оптималь­ного группирования, что гарантирует их макси­мальную мощность при распознавании близких гипотез. В этом случае непара­метрические крите­рии Колмогоро­ва, Смирнова,  и  Мизеса существенно уступают им, если не учитывается факт оценивания по выборке параметров распределения.

3. С учетом вышесказанного параметрический метод отбраковки грубых ошибок измерений позволяет эффективно исключать аномальные наблю­дений.

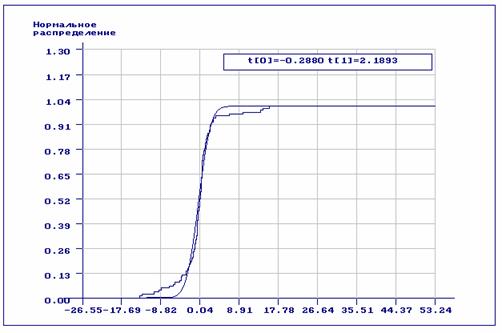
Рис.11. Эмпирическая функция распределения и теоретическая функция нормального закона распределения, най­ден­ная по сгруппированной выборке, принадлежащей распреде­ле­нию Коши.

1.      Хьюбер П. Робастность в статистике. - М.: Мир, 1984. - 303 с.

2.      Орлов А.И. Неустойчивость параметрических методов отбраковки рез­ко выделяющихся наблюдений // Заводская лаборатория. 1992. Т. 58. № 7. С. 40-42.

3.      Лемешко Б.Ю. Статистический анализ одномерных наблюдений слу­чай­ных величин: Программная система / Новосиб. гос. техн. ун-т. -  Новоси­бирск, 1995. 125 с.

4.      Куллдорф Г. Введение в теорию оценивания по группированным и час­тично группированным выборкам. - М.: Наука, 1966. - 176 с.

5.      Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное груп­пи­рование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. 346 с.

6.      Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.

7.      Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

8.      Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория. 1985. Т. 51. № 1. С. 60-62.