Макашов А. В. Анализ эффективности параллельных методов решения задачи Коши для ОДУ

Данное пособие представляет собой систематизированное содержание лекций по курсу? Ведение в численные методы, который читается на втором курсе факультета ВМиК с 1994 г . и содержит последовательное изложение основных понятий, определений, теорем и утверждений, рассматриваемых и доказываемых на лекциях.

Интерполяция и квадратурные формулы

1. Интерполирование

Опр. Пусть функция f(х) задана таблично на [a,b]:

x 0 = a, x n = b , x 0 < x 1 < x 2 < .... < x n , y i = f(x i ) i = 0,..., n

Тогда построение непрерывной на [a,b] функции j (x) , такой что j (x i ) = y i называется интерполяцией функции f(x) на [a,b].

Опр. Пусть полином степени n L n (x) = a 0 x n + a 1 x n-1 + ... + a n интерполирует y=f(x) на [a,b], т.е. L n (x i ) = y i = f(x i ). Тогда L n (x) называется интерполяционным полиномом.

Утверждение. Интерполяционный многочлен степени n для функции y=f(x), заданной таблично в n+1 точках, существует и единственен.

Данное утверждение следует из того, что определитель Вандермонда отличен от нуля.

Существуют некоторые стандартные формы записи интерполяционных полиномов. Интерполяционный многочлен в форме Лагранжа имеет вид

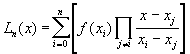Интерполяционный многочлен в форме Ньютона имеет вид

где

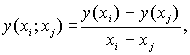
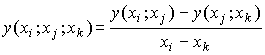
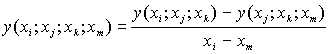. . . - выражения такого вида называются разделенными разностями .

Теорема.

Пусть функция y=f(x) имеет n+1 непрерывную производную на [a,b], и L n (x) - интерполяционный многочлен, L n (x i ) = f(x i ) , i=0,1,...,n. Тогда для погрешности интерполяции y (x) = i L(x) - f(x) i справедлива оценка

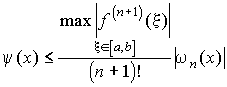
где

Полиномы Эрмита

Полиномы Эрмита интерполируют таблично заданную функцию с учетом известных значений производной в узлах сетки.

Пусть заданы n+1 узлов x i , x 0 = a, x n = b , x 0 < x 1 < x 2 <....< x n , значения функции в них y i = f(x i ) и значения производной в них y i ' = f' (x i ) i = 0,..., n. Требуется построить полином P 2n+1 (x) такой, что P 2n+1 (x i ) = y i , P 2n+1' (x i )= y i ' . Этот полином и называется полиномом Эрмита .

Интерполяция сплайнами

Пусть функция y=f(x) задана таблично :

x 0 = a, x n = b , x 0 < x 1 < x 2 < .... < x n , y i = f(x i ) i = 0,..., n.

Кубической сплайн-интерполяцией называется функция j (x) такая, что

j (x i ) = f(x i ) , i=0,1,...,n ,

j ' (x i -0) = j ' (x i +0) , j ' ' (x i -0) = j ' ' (x i +0) i=1,...,n-1 (1)

j ' ' (x 0 ) =0, j ' ' (x n ) =0,

и j (x) = a i + b i (x-x i ) +c i (x-x i ) 2 +d i (x-x i ) 3 , x i-1 ? x ? x i

Величины коэффициентов a,b,c,d, находятся из системы уравнений (1). Для нахождения значений этих коэффициентов удобно, с помощью последовательного исключения неизвестных, редуцировать систему (1) к системе трехточечных уравнений относительно коэффициентов с i , и решать ее далее с помощью метода прогонки (см. далее).

2. Квадратурные формулы

Выражение вида

предназначенное для вычисления определенного интеграла называется квадратурной формулой.

Величина R=I - S называется погрешностью квадратурной формулы.

Формула прямоугольников

Простая : S 0 = (b-a) f ( (b+a)/2 ) , R 0 = -(b-a) 3 f --( x )/ 24 , x I (a,b)

Составная: , h=(b-a)/n

Формула трапеций

Простая : S 1 = (b-a)( f(b) + f(a) )/ 2, R 1 = (b-a) 3 f --( x )/ 12 , x I (a,b)

Составная: , h=(b-a)/n

Формула Симпсона

Простая : S 2 = (b-a)( f (a) + 4f ( (b+a)/2 ) + f(b) )/ 6,

R 2 = (b-a) 5 f (4) ( x )/ 90 , x I (a,b)

Cоставная: ,

h=(b-a)/n, здесь - четное число.

Формулы Гаусса

В квадратурных формулах Гаусса ищутся не только коэффициенты С i , но и точки x i - из соображений обеспечения точности квадратурной формулы для полинома максимальной степени.

Квадратурная формула Гаусса будет точна для произвольного полинома степени 2n+1,если величины c i и x i удовлетворяют системе уравнений:

Можно показать, что узлы x j квадратурной формулы на отрезке [-1,1] являются корнями полинома Лежандра :

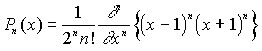
а коэффициенты квадратурной формулы вычисляются по формулам

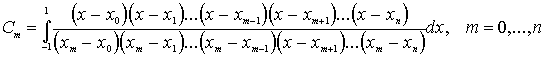
Решение систем линейных уравнений

Постановка задачи

Найти вектор x , удовлетворяющий уравнению

A x = f ,

где A - квадратная матрица порядка n,

A = { a i, j }, i,j = 1,2,...,n, x T = {x 1 ,x 2 ,..., x n }, f T = { f 1 ,f 2 ,...,f n },

или, что тоже самое, найти x 1 ,x 2 ,..., x n удовлетворяющие системе уравнений

a 11 x 1 + a 12 x 2 + ... + a 1n x n = f 1

a 21 x 1 + a 22 x 2 + ... + a 2n x n = f 2

................................................

a n1 x 1 + a n2 x 2 + ... + a nn x n = f n

1. Прямые методы

Метод Гаусса состоит в приведении матрицы к треугольному виду.

Приведение матрицы к треугольному виду осуществляется по формулам

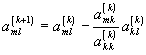
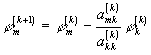, m= k+1,...,n, l= k,..., n, k=1,...,n-1.

(прямой ход метода Гаусса), в результате чего получается система

a (n) 11 x 1 + a (n) 12 x 2 + ... + a (n) kk x k + ... + a (n) 1n x n = j (n) 1

a (n) 22 x 2 + ... + a (n) kk x k + ... + a (n) 2n x n = j (n) 2

....................................................................

a (n) kk x k + ... + a (n) kn x n = j (n) k

....................................................................

a (n) nn x n = j (n) n

Вычисление решения x 1 ,x 2 ,..., x n осуществляется следующим образом

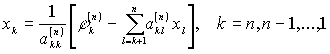
(формулы обратного хода Гаусса)

Общее число действий в методе Гаусса порядка (n 3 +3n 2 )/3.

Метод прогонки

Метод прогонки применяется для решения систем линейных уравнений с матрицей специального вида - трехдиагональной матрицей :

- a i x i-1 + c i x i - b i x i+1 = f i i=2, ... , n-1

x 1 = k 1 x 2 + n 1 (2)

x n = k 2 x n-1 + n 2

На первом этапе находятся коэффициенты

a i+1 = b i /(c i - a i a i ) , b i+1 = ( b i a i + f i ) /(c i - a i a i ) i=2, ... , n-1 (прямой ход), a 2 = k 1 , b 2 = n 1,

а на втором этапе находится решение

x i = a i+1 x i+1 + b i+1 , i = n-1, ... ,2,1

x n = ( n 2 + b n ) / ( 1- a n k 2 ).

Для корректности метода прогонки достаточно, чтобы коэффициенты a i были по модулю меньше единицы, а выражения в знаменателях формул были отличны от нуля. Достаточные условия корректности прогонки формулируются в следующих теоремах.

Теорема

Пусть система уравнений (2) такова, что a i > 0, b i >0, c i >0, c i ? a i + b i , i=2,..., n-1, и i k 1 i + i k 2 i <2, i k 1 i ? 1, i k 2 i ? 1.

Тогда метод прогонки корректен.

Теорема

Пусть система уравнений (2) такова, что a i > 0, b i >0, c i >0, c i ? a i + b i , i=2,..., n-1, и существует i 0 >1 такое, что c i0 > a i0 + b i0 , и i k 1 i ? 1, i k 2 i ? 1.

Тогда метод прогонки корректен .

Теорема

Пусть система уравнений (2) такова, что c a i c , c b i c , c c i c >0, c c i c > c a i c + + c b i c , i=2,..., n-1, и i k 1 i ? 1, i k 2 i ? 1.

Тогда метод прогонки корректен .

2. Итерационные методы

Канонический вид одношаговых итерационных методов для решения системы линейных алгебраических уравнений A x = f :

где В к+1 - квадратная матрица n ¦ n , t k+1 > 0 - итерационный параметр. В дальнейшем будем использовать следующие согласованные нормы в конечномерном пространстве размерности n:

- евклидова норма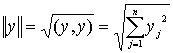

- норма в С

- энергетическая норма A=A * >0

Под нормой матрицы А будем понимать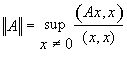

Итерационный метод сходится, если .

Опр. Величина z k = x k - x называется погрешностью решения.

Опр . Если B k+1 = B и t k+1 = t то метод называется стационарным

Теорема .

Пусть A=A * >0, и B- 0.5 t A>0 тогда итерационный метод

сходится в норме e e * e e A , .

Метод Зейделя

Каноническому виду метода Зейделя соответствует B=(D+L), t =1, где D -диагональная матрица, L - нижняя треугольная матрица

Индексный вид метода Зейделя

Теорема

Пусть A=A * >0, тогда метод Зейделя сходится .

Теорема

Пусть матрица A такова, что i=1,..., n, e q e <1, тогда метод Зейделя сходится со скоростью геометрической прогрессии со знаменателем q, т.е.

Метод релаксации

Канонический вид

w < 1- метод нижней релаксации

w = 1- метод Зейделя

w > 1- метод верхней релаксации

Теорема Пусть A=A * >0, 0< w <2, тогда метод релаксации сходится.

Метод простой итерации

Канонический вид метода простой итерации -

Теорема

Пусть A=A * >0, 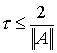, тогда метод простой итерации сходится.

Замечание. Если A=A * >0 то у матрицы А существует n собственных значений l k таких, что

0< l min = l 1< l 2 <...< l n-1 < l n = l max ,

при этом и .

Можно найти оптимальное значение итерационного параметра t = t 0 такое, что заданная точность решения будет достигаться за минимальное число итераций.

Теорема

Пусть A=A * >0, тогда при для погрешности явного метода простой итерации z k справедлива оценка

Основы теории разностных схем

1. Основные понятия

Опр . Пусть дан отрезок [a,b]. Равномерной сеткой на этом отрезке назовем множество узлов w h такое, что w h = { x j = jh, j=0,...,n, h=(b-a)/n) }.

Опр. Сеточной функцией y = y j = y(x j ) называется функция, заданная в узлах сетки.

Любую сеточную функцию y j = y(x j ) можно представить в виде вектора Y=(y 0 , y 1 , ..., y n-1 , y n ), и, следовательно, множество сеточных функций образует конечномерное пространство, в данном случае размерности n+1. В этом пространстве можно ввести норму, например

или .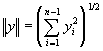

Пусть дано дифференциальное уравнение

Lu(x) = f(x,u) ( например, ) .

Заменим Lu в узле сетки x i линейной комбинацией значений сеточной функции y i на некотором множестве узлов сетки, называемом шаблоном. Такая замена Lu на L h y h называется аппроксимацией на сетке дифференциального оператора L разностным оператором L h . Замена непрерывной функции f(x,u) в узлах сетки на сеточную функцию j (x h ,y h ) называется аппроксимацией правой части.

Таким образом дифференциальное уравнение можно аппроксимировать (заменить) на сетке разностной схемой

L h y h = j ( x h ,y h ) ( например, ).

Изучение разностных аппроксимаций проводится сначала локально, т.е. в любом фиксированном узле сетки.

Пусть u h - проекция непрерывной функции u(x) на сетку ( например, u h = u(x j ) = u j ).

Опр. Погрешностью аппроксимации дифференциального оператора Lu разностным оператором L h назовем величину y 1 = (Lu) h - L h u h , где (Lu) h - проекция на сетку результата действия дифференциального оператора L на функцию u

( например, ) .

Опр. Говорят, что погрешность аппроксимации дифференциального оператора имеет в узле x i порядок k , если y 1 (x i ) = O(h k ) - 0 при h - 0.

Опр. Погрешностью аппроксимации правой части f сеточной функцией j h назовем величину y 2 = f h - j h , где f h - проекция на сетку функции f(x,u) (например, f(x j ,u j ).

Опр. Погрешность аппроксимации правой части имеет в узле x i порядок m , если y 2 = O(h m ) - 0 при h - 0

Опр. Погрешностью аппроксимации разностной схемы на решении в узле x i (локальной погрешностью) назовем величину y , равную

y = y 1 - y 2 = (Lu) h - L h u h - ( f h - j h )= j h - L h u h ,

здесь использовано, что Lu=f.

Опр. Значения локальной погрешности аппроксимации в каждом узле x i образуют сеточную функцию погрешности аппроксимации y i .

Обычно требуется оценка погрешности аппроксимации на сетке, т.е. оценка функции y i в некоторой сеточной норме.

Опр. Говорят, что погрешность аппроксимации разностной схемы имеет m-ый порядок на сетке, если ? e y ? e = O(h m ).

Опр. Решение разностной схемы сходится к решению дифференциального уравнения с порядком k на сетке, если погрешность решения

? e z h ? e = ? e u h - y h ? e = O(h k ) - 0 при h - 0.

2.Методы решения обыкновенных дифференциальных уравнений (ОДУ)

Требуется найти численное решение задачи Коши для ОДУ первого порядка

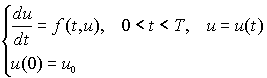
На отрезке [0,T] вводим разностную сетку w t = { t n = n t , n=0,...,N, t =T/N } и сеточную функцию y n = y(t n ).

Метод Эйлера

1 . Явный метод Эйлера.

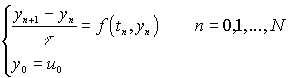
Погрешность аппроксимации явного метода Эйлера y = O( t ) - первого порядка ( y 1 = O( t ), y 2 = 0 ).

Одним из способов повышения порядка сходимости разностных схем для ОДУ является использование методов Рунге-Кутта . Общий вид схем Рунге -Кутта для решения задачи Коши для ОДУ первого порядка имеет следующий :

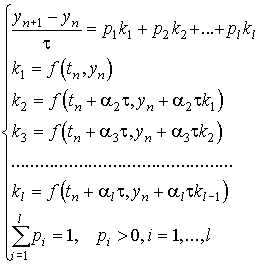
Величины p k и a k выбираются из соображений аппроксимации.

Метод Рунге - Кутта второго порядка

Величины p 1 , p 2 , a определяются из условия второго порядка аппроксимации, для данной схемы p 1 = (2 a -1)/ a , p 2 = 1/2 a .

Метод Рунге- Кутта второго порядка можно записать в другом виде

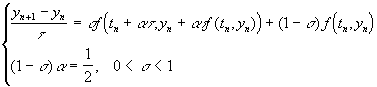
Условие второго порядка аппроксимации (1- s ) a =0.5.

На практике широко распространен Метод Рунге - Кутта четвертого порядка :

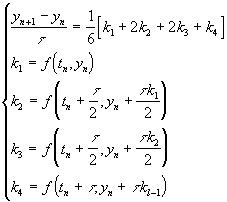
Данная схема имеет четвертый порядок аппроксимации.

Другую возможность для повышения порядка сходимости разностных схем для решения ОДУ предоставляют Методы Адамса.

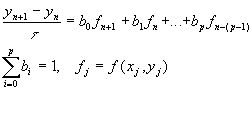
В методах Адамса коэффициенты b i находятся из условий наивысшего для данного p порядка погрешности аппроксимации.

Методы Адамса являются многошаговыми и являются разновидностью p - шаговых методов. P-шаговый метод может быть записан в следующем общем виде:

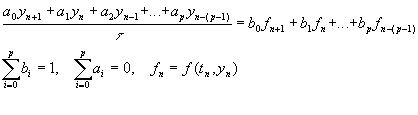
P- шаговому методу Адамса соответствует набор коэффициентов a i вида

a 0 =1, a 1 = -1, a 2 = ... = a p =0

Явный двухшаговый метод Адамса.

Погрешность аппроксимации имеет второй порядок. Для нахождения y 1 (со вторым порядком) используется обычно схема Рунге-Кутта второго порядка.

Неявный двухшаговый метод Адамса.

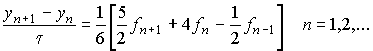
Погрешность аппроксимации имеет третий порядок . Для начала решения задачи Коши для ОДУ первые p шагов нужно сделать с помощью какого-либо другого метода, например, метода Рунге - Кутта.

3. Разностная схема для решения краевой задачи второго порядка

Рассмотрим задачу для уравнения второго порядка с краевыми условиями первого рода

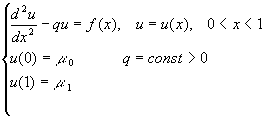Разностная аппроксимация второй производной на равномерной сетке w h простейшего вида имеет второй порядок аппроксимации:

Тем самым разностная схема второго порядка аппроксимации для краевой задачи с краевыми условиями первого рода имеет вид:

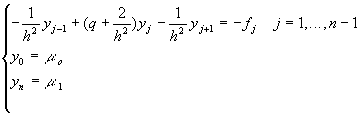
Данная разностная схема может быть решена при помощи метода прогонки, который устойчив при q>0. Для применения метода прогонки разностную схему удобно переписать в виде

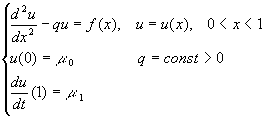
На практике часто встречается задача с краевыми условиями первого и второго рода:

Разностная схема аппроксимирующая краевую задачу с краевым условием второго рода требует специальной аппроксимации первой производной в краевом условии со вторым порядком аппроксимации:

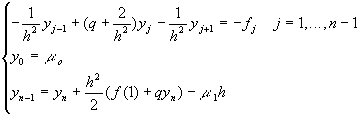
При аппроксимации первой производной использован тот факт, что исходное дифференциальное уравнение справедливо и в точке x=1. Решение данной разностной схемы может быть получено с помощью метода прогонки, для чего удобно записать разностную схему в виде:

4. Разностная задача на собственные значения

Дифференциальная задача Штурма-Лиувилля

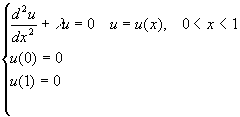
Числа l и соответствующие функции u(x) ¦ 0, удовлетворяющие поставленной краевой задаче называются собственными числами и собственными функциями соответственно. Для данной задачи

Заметим, что функции u m ( x ) являются линейно независимыми и взаимно ортогональными и могут быть нормированы.

Для разностной задачи на собственные значения

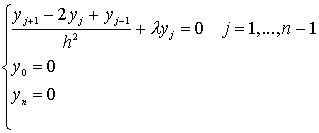
соответствующие собственные функции и собственные значения разностной задачи имеют вид

Заметим, что функции y m ( x ) являются линейно независимыми и взаимно ортогональными, как и в дифференциальном случае, и могут быть нормированы.

Литература.

А.А. Самарский, А.В. Гулин. Численные методы. М., Наука, 1989

Н.С.Бахвалов, Н.П. Жидков, Г.М.Кобельков. Численные методы. М., Наука, 1987

А.А.Самарский, Е.С.Николаев. Методы решения сеточных уравнений. М., Наука, 1978

Н.Н. Калиткин. Численные методы. М., Наука, 1978

вернуться к оглавлению