One of the first papers to provide a general parallel ODE method seems to that of Miranker and Liniger. They consider linear multistep methods with correctors. (Explicit linear multistep methods have poor stability and so are usually used with one or more corrector steps.) For example the Adams method in the usual form can only be executed sequentially

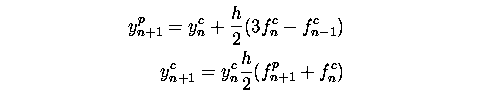
But by considering a modification to the predictor a new formula is written

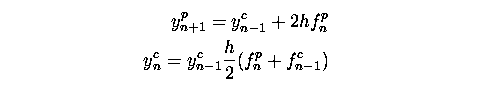
The corrector step is the same as above except all the subscripts refer to the previous step's predictor values. The predictor is less accurate because it uses two Euler method steps from the (n-1)^th value. But the two formulae can be evaluated in parallel. This can be generalised to a class of multistep methods that can execute in parallel on 2s processors, where in each iteration the solution is advanced s values. Since the predictors are relying on older data the methods will be less accurate and so for the same accuracy the step size must be reduced and, in general, the speedup will less than a factor of 2s. Methods of various orders were tested by observing the dependence of the global error on the step size for a particular problem. It was found in the two processor case that the methods performed almost as well their sequential counterparts. If communication overheads could be neglected this would mean the methods would provide a twofold speedup. For four processors on the same test, results were more variable ranging from a potential speedup of two to more than four (i.e. the method was more accurate than sequential method for a particular parameter value on a test problem.)

Worland considers a different class of methods known as one step block implicit methods. Block methods generate a series of estimates for f in the next interval (t, t+h], each point being calculated in terms of previous points in the interval. The methods considered here calculate k points, each a distance h apart. An initial prediction of the value at t+rh is made using an open Newton-Cotes formula in terms of the previous r points. The value is then corrected a number of times using a fixed point iteration on a closed Newton-Cotes formula with the predictor as initial estimate. This is illustrated using the two point, third order method

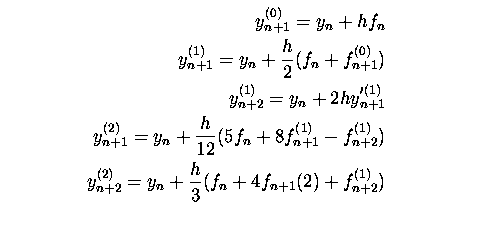
These formulae are essentially using Gauss-Seidel iteration on the correction steps. If the predictor steps are modified to use Euler integration from the start value and the iteration is changed to Gauss-Jacobi iteration the following formulae can be generated.

where s = 0,1,2. More function evaluations are required but the calculation of y_n+1 and y_n+2 can proceed in parallel. Increased parallelism can be obtained by increasing the number of points, k, in the block, which increases the order. Typical theoretical speedups, compared to sequential versions of these methods, are 1.7 for a 2 processor, third order method or 2.8 for 4 processor fourth order method.

The author goes on to consider block predictor-corrector schemes. Here values from the previous block are used to predict the values for the current block. The current values are then refined, or corrected, by iteratively applying formulae. As in the simple block method above the iteration can Gauss-Seidel or Gauss-Jacobi depending on whether the algorithm is the sequential or the parallel version.

Franklin developed a practical execution time model for the methods above and for parallel evaluation of the components of y (equation segmentation in his terminology, parallelism across the system in Gear's). The inputs to the model are the timings for the function evaluation, times to evaluate a predictor or corrector formula, communication time and synchronisation time (this would be the communication startup time in modern parlance). Execution times, using the two processor formula, are them predicted using values from a DEC PDP 11/45 and number of standard benchmark problems. The predictor-corrector methods of Miranker and Liniger have the same predicted performance as those of Worland and in general achieve speedups varying from 1.8 to nearly 2. The equation segmentation procedure is slightly less successful because of the impossibility of achieving a perfect workload balance over both processors.

The two methods considered have been shown to have some disadvantages. The predictor-corrector methods of Miranker and Liniger have poor global error behaviour. Also no attempt appears to have been made to develop variable step size implementations of the methods. Variable step size methods exist for the sequential predictor-corrector methods used in Worland but the parallel versions are poorly behaved, Burrage. Both of these methods offer only a small amount of parallelism.

The systematic study of parallel methods for ODEs seems to have started with Gear. Gear introduces the terms parallelism across the system and parallelism across the method. The first term is the equation segmentation discussed by Franklin. In this case, would represent a vector of quantities and the calculation of different components of the vector can be split amongst a number of processors. How easy and successful this will be will depend critically on the nature of the system and how much communication is required between different components. In particular, for stiff systems requiring implicit methods, the communication overhead is likely to be high. This demonstrated by considering the backward Euler, applied to the linear system

Unless the system can be decoupled in some way, then it is nearly always true that the matrix (I - hA)^-1 will have no zeros in it. This means that to calculate a component of the next value then every component from the previous value needs to be communicated to it. The problem is worse in the non-linear case when is replaced by several Newton-Raphson iterations.

Another problem occurs in a variable step size method when the next step size is being calculated. The step size selection requires a calculation of the current local error which must be done by calculating a quantity like , where , is some intermediate estimate of the solution. Because this quantity is a scalar it must ultimately involve a serial calculation and the step size selection algorithm itself must be serial.

Of course, the even distribution of workload across processors is another problem. This is very much domain dependent but as will be seen below even with very regular problems workload imbalance can be an impediment to performance.

The second type of parallelism, parallelism across the method, means exploiting parallelism across subtasks within the method itself. The methods of Miranker and Worland are examples of such methods. Another important class of such methods are the Runge-Kutta methods, to be discussed in more detail below. In this case the parallelism is inherent in the method itself and can even be applied to one dimensional systems. These have the advantage that there is no loss of performance due to workload. However, they only offer limited parallelism and, in general, increases in parallelism are only gained for higher order methods.

Назад