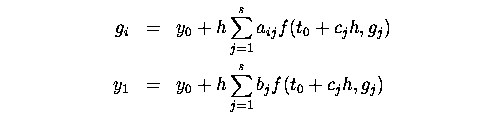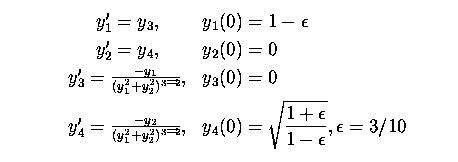Parallel Runge-Kutta methods, as examples of parallelism across the method, are reviewed in more detail here. The reasons are that parallel versions have been widely studied, they are well understood, and some experiments on modern computer systems have been reported in the literature. In addition efficient variable step size methods exist, both parallel and serial, that are easy to implement.

A Runge-Kutta method has the following form:

where a_ij, b_i and c_i are constants that define the method. This is an s stage Runge-Kutta method. If matrix A, where A_ij = a_ij is strictly lower diagonal then the method is an explicit method. That is each g_i only depends only on other g_j where j < i, g₁ = y₀ and so each g_i can be calculated using values calculated in previous steps, without having to solve algebraic equations involving f. For example, the classic Runge-Kutta formula is:

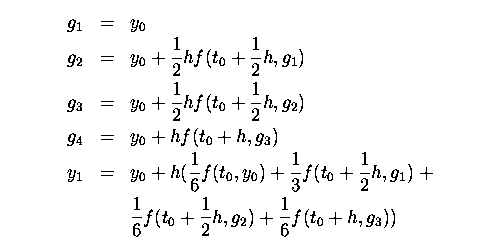
In this case there is no opportunity for parallelism. Each calculation relies on results from the calculation immediately before. The following 3^rd order method :

has a small opportunity for parallelism in that g₂ and g₃ can be calculated together.

The number of sequential stages of a method is the maximum number of function evaluations that must be performed sequentially. In general the following theorem shows limits of parallelism for explicit Runge-Kutta methods.

Methods with p=q are called P-optimal. They are optimal because they can achieve the theoretical limit of having the order of the method equal to the number of sequential stages. This the only way to achieve a speedup using parallelism with explicit Runge-Kutta methods. The minimum number of processors required to achieve the maximum speedup does not appear to be known.

The authors van der Houwen and Sommiejer show how such methods can be constructed. They suggest using the A matrix from an implicit method where the underlying implicit method has order p₀=2s and then solving the resulting non-linear algebraic equations by fixed point iteration. For each iteration the s function evaluations can proceed in parallel, the method runs on s processors. This looks like

Appropriate implicit methods can be constructed to arbitrary order so the parallel methods can also be constructed to arbitrary order. These methods are known as parallel iterated Runge-Kutta methods, or PIRKs. For example the most efficient known 10^th order method has 17 stages, i.e. it requires 17 function evaluations. By using a 5 stage, 10^th order implicit method as the basis, a parallel method requiring 10 steps and executing on 5 processors can be constructed.

The order of the iterated method is p=min(m+1, p₀) so only m = p₀-1 iterations are considered. Each fixed point iteration equation can be solved independently thus, for optimal parallelism, s processors can be used. As an aside the fixed point iterations destroy the stability properties of the implicit method.

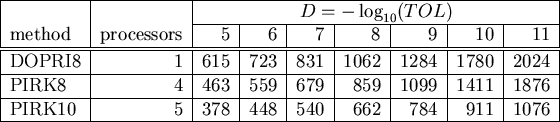
Some experiments with PIRKs are reported in the literature. Van der Houwen and Sommiejer were concerned to show that their methods can achieve the predicted levels of accuracy with fewer sequential steps. The intention was to demonstrate mathematical performance at this stage rather than "real world'' performance, with all its associated implementation and specific domain issues. The authors select three problems from the literature and compare their 10^th order PIRK codes against DOPRI8. The code DOPRI8 was, at that time, one of the most efficient general codes for high accuracy, non-stiff problems. Both codes use an embedded lower order method for step size control. The tests were performed for tolerances ranging from 10^-5 to 10^-12 and the number of sequential steps required was reported. As an example Table reproduces the results for the orbit equations.

Comparison between PIRK8 and DOPRI8 shows the performance improvements are in the expected range. The method used in DOPRI8 has 13 stages while the PIRK8 has 8. The PIRK10 code performs better but this is because it is higher order. The authors point out that PIRKs are also of interest because they can be constructed to arbitrary order, they have embedded methods for step size control and the order can be easily varied (by reducing the number of iterations) to increase efficiency, if the problem allows.

Figure: The number of sequential steps required to solve for tolerances 10^-D. The column titled processors indicates the number of processors that would be required to achieve the number of sequential steps.

An experiment using a combination of a PIRK and parallelism across the system is that of Rauber and Runger. These authors construct an analytical model of the expected performance for a number of algorithms on the Intel iPSC/860, a distributed memory parallel computer. The systems of equations considered are from the spatial discretisation of partial differential equations, which generates a large system. Parallelism is achieved not only by performing the functional iterations in parallel (parallelism across the method), as above, but also by evaluating different components of the functions in parallel (parallelism across the system). The global execution time model is constructed based on the execution time for each component of the function, the dimension of the system, communication times between nodes, cost of the step size control, number of processors and can be applied to each of the algorithms considered.

Two systems of equations are considered. The Brusselator, a chemical reaction and diffusion equation and a perennial favorite amongst applied mathematicians. This has a constant function evaluation time per component independent of the size of the system. The second system resulted "from the numerical solution of a one dimensional Schrudinger-Poisson system with a Galerkin-Fourier method''. The interesting feature of this system is that the function evaluation time is O(n²) in the size of the system, rather than the more usual O(n). The PIRK used is based on a 5^th order, 3 stage Radau method with 4 functional iterations. This executes on three processors. The authors partition the processors into groups, each group performing a function evaluation in parallel with the others. Components of the function are distributed across processors within each group. The three algorithms considered have different arrangements of the communication phases. The results are in very good agreement with the execution time model. The system with linear function evaluation time achieved a far better speedup than the system with constant function evaluation time. This is because the data communication costs remained high compared to the function evaluation costs even for a large system ( n ~10000). The speedups for the largest systems are shown in Table.

Figure: This table shows speed-ups achieved for systems with dimension of 10,000 and the best of the three algorithms. The sequential method used for comparison was the sequential version of the PIRK. Results are from Rauber and Runger.

The performance on the Brusselator system was comparatively poor. This is because the inexpensive function evaluation time is small relative to the time required for data communication. The algorithms considered by the authors are generic in that they can be blindly applied to any system of ODEs. This means that at the end of each function evaluation every component of the function must be communicated to every node. For large systems like the ones considered here this means a lot of data communication. In the case of systems arising from the discretisation of partial differential equations most of this communication is unnecessary, because each grid point only couples to its nearest neighbors. The authors show for the Brusselator in two spatial dimensions, discretised into a grid with N points on each side, then if the number of processors satisfy N>=p then each processor needs to only communicate with at most two other processors. After implementing these problem specific improvements speedups of 2, 3.4 and 5 were achieved on 4, 8 and 16 processors respectively. This result for the Brusselator is interesting because it appears to be a difficult system in which to achieve good levels of parallelism. The method presented here can be compared to the waveform relaxation method on the same problem, summarized below.

This work is interesting for a number of reasons. Firstly, it shows how to construct a model of the global execution time, if the problem is sufficiently regular. Secondly by comparing three general ODE algorithms and two algorithms tailored to the problem it shows the importance the data communication protocol. Unfortunately it is difficult to interpret the speedup results as they stand. The speedups quoted are the ratio of the parallel algorithm to the sequential form of the PIRK algorithm. A better comparison would be to a sequential algorithm of similar order. The authors point out that the appropriate sequential algorithm is the 5^th order Fehlberg method and give a relative speedup of the Fehlberg method to the PIRK but it is not clear how to combine this with their speedup values.

The poor performance of the constant time function illustrates an interesting point. The system is quite large, of the order of 10⁴, but even so the data communication costs dominated. The algorithms considered were required to communicate data between the processors after each function evaluation, that is 5 times per integration step. As will be seen one of the advantages of waveform relaxation is that the data communication is comparatively small.

Назад