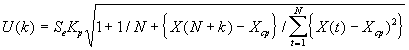 (1)
(1)3. Построение точечного и интервального прогнозов для моделей регрессии
При использовании построенной модели регрессии для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.
Для прогнозирования зависимой переменной на
k шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель и получаются прогнозные оценки.Для того чтобы определить область возможных значений результативного показателя, при рассчитанных значениях факторов следует учитывать, два возможных источника ошибок: рассеивание наблюдений относительно линии регрессии и ошибки, обусловленные математическим аппаратом построения самой линии регрессии. Ошибки первого рода измеряются с помощью характеристик точности, в частности, величиной Sе. Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.
Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):
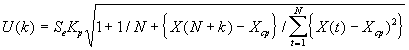 (1)
(1)
Коэффициент Кр является табличным значением
t- статистики Стьюдента при заданном уровне значимости и числа наблюдений. Если исследователь задает уровень вероятности попадания прогнозируемой величины внутрь доверительного интервала, равный 70%, то Кр=1.05. Если 95%, то Кр=1.96, а при 99% - Кр= 2.65.Как видно из формулы (1) величина
U прямо пропорционально зависит от точности модели, коэффициента доверительной вероятности Кр , степени удаления прогнозной оценки фактора X и обратно пропорциональна объему наблюдений.В результате получаем следующий интервал прогноза для шага прогнозирования
k:верхняя граница прогноза
= Y(N+k)+U(k),нижняя граница прогноза
= Y(N+k)- U(k).Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.

