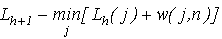Алгоритм Беллмана-Форда.

Алгоритм Беллмана-Форда может быть сформулирован следующим образом. Требуется найти кратчайшие пути от заданной вершины при условии, что эти пути состоят максимум из одного ребра, затем найти кратчайшие пути при условии, что эти пути состоят максимум из двух ребер и т.д. Для описания алгоритма введем следующие обозначения:

• s - вершина-источник;
• w(i,j) - стоимость линии от вершины i до вершины j, причем w(i,i)=0 или w(i,j)=, если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;
• h - максимальное количество ребер в пути на текущем шаге алгоритма;
• L_h(n) - минимальная стоимость пути от вершины s до вершины n при условии, что этот путь состоит не более чем из h ребер.

1. Инициализация
   L₀(n)= для всех n<>s,
   L_h(s)=0 для всех h.
2. Обновление
   Для каждого последовательного h>=0 и для каждого n<>s вычислить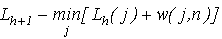
   Соединить вершину n с предыдущей вершиной j, для которой находится минимальное значение, и удалить любое соединение вершины n с предыдущей вершиной, образованное на более ранней итерации. Путь от вершины s до вершины n заканчивается линией связи от вершины j до вершины n.