Алгоритм Дейкстры
Алгоритм находит кратчайшие пути от данной вершины-источника до всех остальных вершин, перебирая пути в порядке увеличения их длин.
Введем обозначения:
- N - множество вершин сети;
- s - вершина-источник;
- T - множество вершин уже обработанных алгоритмом;
- Дерево - связующее дерево для вершин, принадлежащих множеству T, включая ребра, входящие в пути с наименьшей
стоимостью от вершины s до каждой вершины множества T;
- w(i,j) - стоимость линии от вершины i до вершины j, причем w(i,i)=0
или w(i,j)=
 , если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;
, если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;
- L(n) - минимальная стоимость пути от вершины s до вершины n, известного на данный момент алгоритму (по
завершении работы алгоритма это минимальная стоимость пути от вершины s до вершины n).
Алгоритм состоит из трех шагов.Шаги 2 и 3 повторяются до тех пор, пока множество T не совпадает с множеством N.
Это значит, что шаги 2 и 3 повторяются, пока для всех вершин сети не будут найдены окончательные пути.
- Инициализация
T=Дерево={s}, то есть множество исследованных вершин состоит пока что
только из вершины источника.
L(n)=w(s,n) для n<>s, то есть стоимости начальных путей к соседним
вершинам представляют собой просто стоимости линий связи.
- Получить следующую вершину
Найти следующую вершину, не принадлежащую множеству T и имеющую путь
от вершины s с минимальной стоимостью, и включить эту вершину во множество
T и в Дерево. Кроме того, к дереву добавляется ребро, инцидентное
этой вершине и вершине множества Т, входящей в путь с минимальной стоимостью.
Это может быть сформулировано следующим образом. Найти вершину x  T
такую, что
T
такую, что
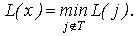
Добавить вершину x к множеству Т и к дереву, добавить к дереву ребро, инцидентное вершине x, составляющее
компонент пути L(x) с минимальной стоимостью, то есть последний ретрансляционный участок пути.
- Обновить путь с минимальной стоимостью
L(n)=min[L(n),L(x)+w(x,n)] для всех n T.
T.
Если последняя величина минимальна, то с этого момента путь от вершины s до вершины n представляет собой конкатенацию пути от
вершины s до вершины x и пути от вершины x до вершины n.
Алгоритм завершает работу, когда все вершины добавлены к множеству T.
 , если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;
, если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую; , если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;
, если две вершины не соединены напрямую, и w(i,j)>=0, если две вершины соединены напрямую;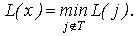
 T.
T.